Homework 4. KenKen solver

Motivation

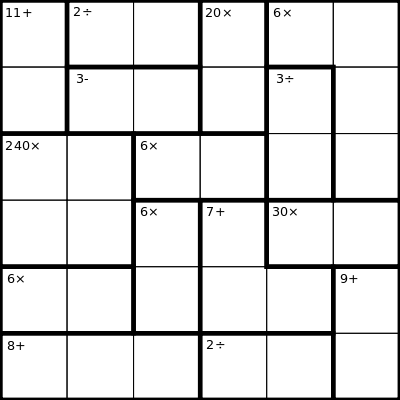
KenKen is an arithmetical-logical puzzle whose goal is to fill in an N×N grid with integers, so that every row and every column contains all the integers from 1 through N, and so that certain extra constraints can be met. These extra constraints are that 1 or more cells must add up to a certain value, or must yield a certain value when multiplied; or that two cells must yield a certain value when divided or subtracted. For example:

Image credit

A human doing this puzzle can reason it out with arguments like the following. The "11+" at upper left must contain a 5 and a 6, as must the "30×" at medium right. Therefore, there cannot be another 5 in either column 1 or row 4. The "240×" at medium left must contain a 5 somewhere, and since it can't be in either column 1 or row 4, the entry in row 3, column 2 must be where the 5 is; we have now deduced an entry. For fun, you might try filling out the rest of the puzzle, using similar reasoning.

A computer solving this problem doesn't need to be that smart. It can rely on a small list of solution strategies rather than the ad hoc approach taken by humans.

Assignment

Write a predicate kenken/3 that accepts the following arguments:

1. N, a nonnegative integer specifying the number of cells on each side of the KenKen square.
2. T, a list of list of integers. All the lists are have length N. This represents the N×N grid.
3. C, a list of numeric constraints as describ

Each constraint in C is of the following form:

+(S, L)

means the integer S is the sum of the list of integers L.

*(P, L)

means the integer P is the product of the list of integers L.

−(D, J, K)

means the integer D is the difference between J and K; D could be equal to either J−K or to K−J.

/(Q, J, K)

means the integer Q is the quotient of J and K; Q could be equal to either J÷K or to K÷J. The remainder must be zero.

Preconditions. N must be a ground term, that is, it cannot be a logical variable or a term containing any logical variables. It must also be a nonnegative integer. The first argument to each constraint, as described below, must also be a ground term that is a nonnegative integer that is less than the current value of vector_max in the GNU Prolog finite domain solver. Your code need not check these preconditions; it can assume that the the preconditions hold.

Other arguments of constraints, and the grid itself, may contain logical variables, which all represent integers that kenken/3 should fill in, or (in the case of the grid) can represent entire rows, or the entire grid.

Example

Suppose you have the following fact; it represents the above KenKen diagram.

kenken_testcase(
  6,
  [
   +(11, [A1,B1]),
   /(2, A2, A3),
   *(20, [A4,B4]),
   *(6, [A5,A6,B6,C6]),
   -(3, B2, B3),
   /(3, B5, C5),
   *(240, [C1,C2,D1,D2]),
   *(6, [C3,C4]),
   *(6, [D3,E3]),
   +(7, [D4,E4,E5]),
   *(30, [D5,D6]),
   *(6, [E1,E2]),
   +(9, [E6,F6]),
   +(8, [F1,F2,F3]),
   /(2, F4, F5)
  ],
  [
   [A1,A2,A3,A4,A5,A6],
   [B1,B2,B3,B4,B5,B6],
   [C1,C2,C3,C4,C5,C6],
   [D1,D2,D3,D4,D5,D6],
   [E1,E2,E3,E4,E5,E6],
   [F1,F2,F3,F4,F5,F6]
  ]
).

Then, the query:

?- fd_set_vector_max(255),
   kenken_testcase(A,B,C),
   kenken(A,B,C).

should output:

A = 6
B = [11+[5,6],/(2,6,3),20*[4,5],6*[1,2,3,1],-(3,1,4),/(3,2,6),240*[4,5,3,4],6*[2,3],6*[1,6],7+[2,1,4],30*[5,6],6*[2,3],9+[5,4],8+[1,2,5],/(2,6,3)]
C = [[5,6,3,4,1,2],[6,1,4,5,2,3],[4,5,2,3,6,1],[3,4,1,2,5,6],[2,3,6,1,4,5],[1,2,5,6,3,4]] ?

and if you respond with a ";" the next result should be "no".

Here's another example, of a puzzle that is not valid for strict KenKen because it has multiple solutions. Your solver should be able to generate all the solutions:

kenken(
  4,
  [
   +(6, [A1,A2,B1]),
   *(96, [A3,A4,B2,B3,B4]),
   -(1, C1, C2),
   -(1, D1, D2),
   +(8, [C3, D3, D4]),
   *(2, [C4])
  ],
  [
   [A1,A2,A3,A4],
   [B1,B2,B3,B4],
   [C1,C2,C3,C4],
   [D1,D2,D3,D4]
  ]
), write([
   [A1,A2,A3,A4],
   [B1,B2,B3,B4],
   [C1,C2,C3,C4],
   [D1,D2,D3,D4]
  ]), nl, fail.

This should output:

[[1,2,3,4],[3,4,2,1],[4,3,1,2],[2,1,4,3]]
[[1,2,4,3],[3,4,2,1],[4,3,1,2],[2,1,3,4]]
[[2,1,3,4],[3,4,2,1],[4,3,1,2],[1,2,4,3]]
[[2,1,4,3],[3,4,2,1],[4,3,1,2],[1,2,3,4]]
[[3,1,2,4],[2,4,3,1],[4,3,1,2],[1,2,4,3]]
[[3,2,4,1],[1,4,2,3],[4,3,1,2],[2,1,3,4]]

no

Submit a file named kenken.pl. If any extra text information is needed, other than what's in the comments, please submit it as a separate text file.