Homework 4. KenKen solver

Motivation

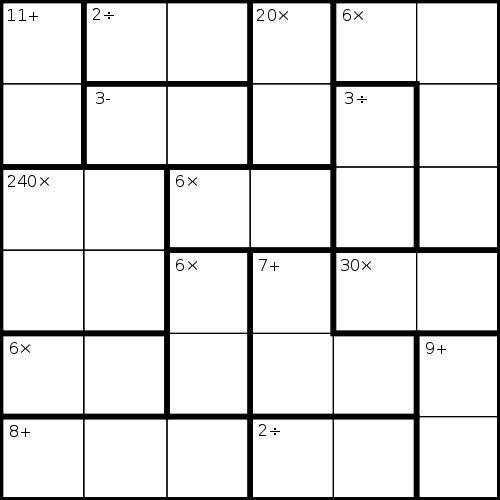
KenKen is an arithmetical-logical puzzle whose goal is to fill in an N×N grid with integers, so that every row and every column contains all the integers from 1 through N, and so that certain extra constraints can be met. These extra constraints are that 1 or more cells must add up to a certain value, or must yield a certain value when multiplied; or that two cells must yield a certain value when divided or subtracted. For example:

Image credit

A human doing this puzzle can reason it out with arguments like the following. The "11+" at upper left must contain a 5 and a 6, as must the "30×" at medium right. Therefore, there cannot be another 5 in either column 1 or row 4. The "240×" at medium left must contain a 5 somewhere, and since it can't be in either column 1 or row 4, the entry in row 3, column 2 must be where the 5 is; we have now deduced an entry. For fun, you might try filling out the rest of the puzzle, using similar reasoning.

A computer solving this problem doesn't need to be that smart. It can rely on a small list of solution strategies rather than the ad hoc approach taken by humans.

Assignment

Write a predicate kenken/3 that accepts the following arguments:

1. N, a nonnegative integer specifying the number of cells on each side of the KenKen square.
2. C, a list of numeric constraints as described below.
3. T, a list of list of integers. All the lists are have length N. This represents the N×N grid.

Each constraint in C is of the following form:

+(S, L)

means the integer S is the sum of integers in the list L of squares.

*(P, L)

means the integer P is the product of the integers in the list L of squares.

−(D, J, K)

means the integer D is the difference between the integer j in square J and the integer k in square K; D could be equal to either j−k or to k−j.

/(Q, J, K)

means the integer Q is the quotient of the integer j in square J and the integer k in square K; Q could be equal to either j÷k or to k÷j. The remainder must be zero.

In the above description, a square is a term i-j where i and j are row and column indexes in the range 1 through N, inclusive. The indexes identify the square in the KenKen diagram that is affected by the constraint in question. The bottom left square is N-1 and the top right square is 1-N.

Preconditions. N and C must be ground terms, that is, they cannot be logical variables or terms containing any logical variables. N must also be a nonnegative integer. The first argument to each constraint, as described below, must be a nonnegative integer that is less than the current value of vector_max in the GNU Prolog finite domain solver. Your code need not check these preconditions; it can assume that the the preconditions hold.

T may contain logical variables, which can represent integers that kenken/3 should fill in, or can represent entire rows, or the entire grid.

Examples

As a trivial example, kenken(1,[],T) should generate just one answer, T=[[1]]. Slightly less trivially, kenken(2,[],T) should generate two answers, T = [[1,2],[2,1]] and T = [[2,1],[1,2]]. With no constraints, the number of answers grows rapidly with N: for example, kenken(3,[],T) should generate 12 answers, and kenken(4,[],T) should generate 576 answers.

Real KenKen puzzles use constraints to narrow the number of solutions to one. Suppose you have the following fact; it represents the above KenKen diagram.

kenken_testcase(
  6,
  [
   +(11, [1-1, 2-1]),
   /(2, 1-2, 1-3),
   *(20, [1-4, 2-4]),
   *(6, [1-5, 1-6, 2-6, 3-6]),
   -(3, 2-2, 2-3),
   /(3, 2-5, 3-5),
   *(240, [3-1, 3-2, 4-1, 4-2]),
   *(6, [3-3, 3-4]),
   *(6, [4-3, 5-3]),
   +(7, [4-4, 5-4, 5-5]),
   *(30, [4-5, 4-6]),
   *(6, [5-1, 5-2]),
   +(9, [5-6, 6-6]),
   +(8, [6-1, 6-2, 6-3]),
   /(2, 6-4, 6-5)
  ]
).

Then, the query:

?- fd_set_vector_max(255), kenken_testcase(N,C), kenken(N,C,T).

should output this (reindented to fit on a printed page):

C = [11+[1-1,2-1], /(2,1-2,1-3), 20*[1-4,2-4], 6*[1-5,1-6,2-6,3-6],
     -(3,2-2,2-3), /(3,2-5,3-5), 240*[3-1,3-2,4-1,4-2], 6*[3-3,3-4],
     6*[4-3,5-3], 7+[4-4,5-4,5-5], 30*[4-5,4-6], 6*[5-1,5-2],
     9+[5-6,6-6], 8+[6-1,6-2,6-3], /(2,6-4,6-5)]
N = 6
T = [[5,6,3,4,1,2],
     [6,1,4,5,2,3],
     [4,5,2,3,6,1],
     [3,4,1,2,5,6],
     [2,3,6,1,4,5],
     [1,2,5,6,3,4]] ?

and if you respond with a ";" the next result should be "no".

Here's another example, of a puzzle that is not valid for strict KenKen because it has multiple solutions. Your solver should be able to generate all the solutions:

kenken(
  4,
  [
   +(6, [1-1, 1-2, 2-1]),
   *(96, [1-3, 1-4, 2-2, 2-3, 2-4]),
   -(1, 3-1, 3-2),
   -(1, 4-1, 4-2),
   +(8, [3-3, 4-3, 4-4]),
   *(2, [3-4])
  ],
  T
), write(T), nl, fail.

This should output:

[[1,2,3,4],[3,4,2,1],[4,3,1,2],[2,1,4,3]]
[[1,2,4,3],[3,4,2,1],[4,3,1,2],[2,1,3,4]]
[[2,1,3,4],[3,4,2,1],[4,3,1,2],[1,2,4,3]]
[[2,1,4,3],[3,4,2,1],[4,3,1,2],[1,2,3,4]]
[[3,1,2,4],[2,4,3,1],[4,3,1,2],[1,2,4,3]]
[[3,2,4,1],[1,4,2,3],[4,3,1,2],[2,1,3,4]]

no

Submit

Submit a file named kenken.pl. If any extra text information is needed, other than what's in the comments, please submit it as a separate text file.