The gzip program was written by Jean-loup Gailly and Mark Adler, who according to Professor Eggert, didn't know jack about programming. But they did know about compression (also they pulled a disappearing act after they finished the program). So Professor Eggert has been maintaining this program for the past couple of decades. Recently, he received a bug report for gzip that claimed gzip would, upon crash, delete the file to be compressed, and fail to output a compressed *.gz file (resulting in user data loss).
The command gzip foo compresses a file foo into another called foo.gz, and removes the original file. The outline of gzip and the system calls it uses is as follows:
1 int ifd = open("foo", O_RDONLY) //input_file_descriptor
2 ofd = open("foo.gz", O_WRONLY | P_CREAT | O_EXEC) //output file descriptor
3 while input file is not completely read: //check for IO errors, stop if there is, and delete foo.gz
4 read(ifd, bf, bufsize)
5 compression()
6 write(ofd, buf, compressed_size_of_bufsize)
7 if (close(ifd) != 0) error()
8 if (close(ofd) != 0) error()
9 if (unlink("foo") != 0) error()
10 exit(0)
In the program, if gzip crashes between line 10 and 11, we lose all data (both the uncompressed and original file). We do all of the correct checks though, yet according to Eggert, this bug is common in many Linux programs. To understand this bug, we must first understand how file systems are implemented, and come back to it at the end of this lecture.
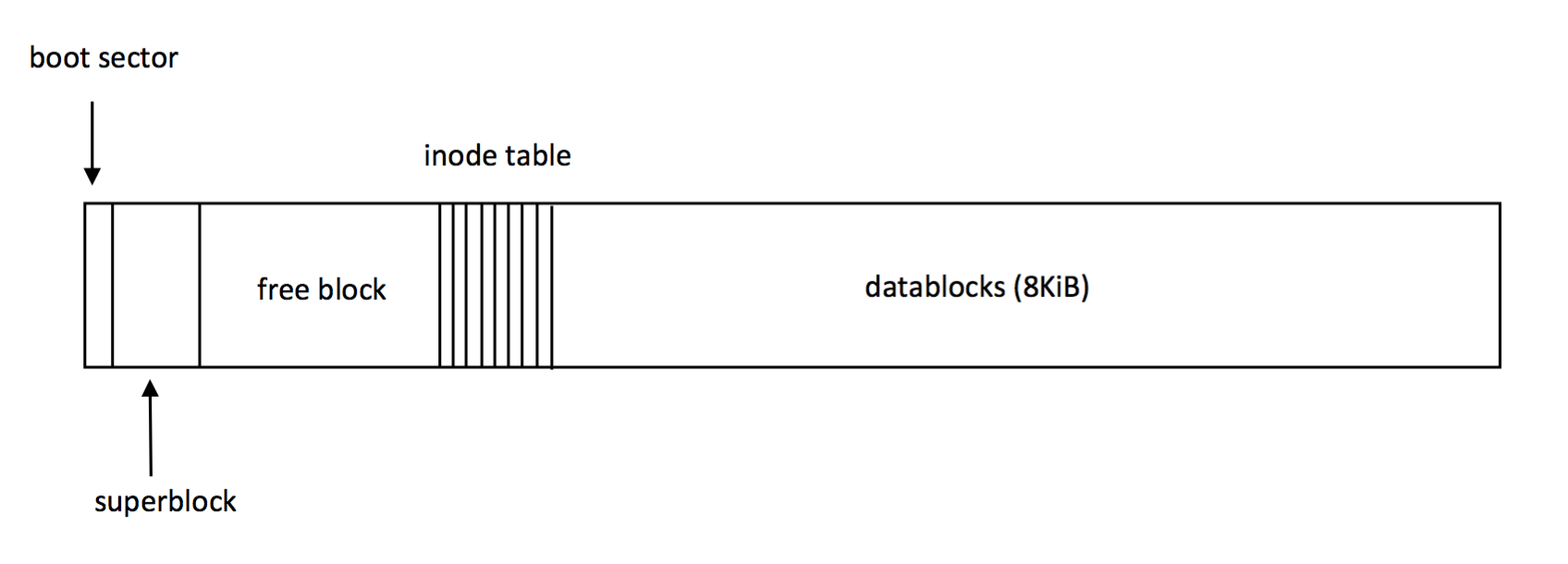
If we recall, the BSD file system layout can be thought of as a disk separated into data blocks. These blocks make up sectors with different uses. The sectors are as follows:

One concern is how to allocate extra space for a file quickly. When we create a file, we give it an initial size that may be exceeded as we write to it. If we want to expand a file beyond its current size, we need to find a free data block. The naive way (First Come First Serve or FCFS) to find a free block is to linear search through the inode table and follow their data pointers to find every block that's in use. Then, we subtract the occupied data blocks to find all the free blocks. The problem with this approach is that it is SLOW. We need to search through a large portion of our file system just so we can add a single block of data to a file. A much better way makes use of the free block bitmap.
The free block bitmap is simply a bitmap that represents all of the in use blocks of the disk. One bit in the bitmap represents a block in the file system. With this approach in a BSD implementation, we need one bit per 8 KiB. If block is free, its representative bit in the bitmap will be set to 1. If it is in use, the bit is set to 0.
Now, we simply traverse the free block bitmap until we find a bit set to 1. We then know that block is free, and can easily give that block to the file that needs to be grown. Bonus points for this solution since we can plausibly cache the entire bitmap in RAM, rather than make expensive read calls to the device.
Note: The boot sectors, super blocks, inode tables, and the free block bitmap itself are represented in the free block bitmap. These blocks are always in use. If we ever tried to give a file a block from these sectors, bad things happen.
Files are stored on the disk, so we need to complete the following steps to read a file from disk and put it into RAM. The approximate amount of time this takes is as follows:
In total, we spend ~18 ms to read a file from disk, the majority of which is overhead. Assuming our machine is clocked at 1 GHz (low estimate of 1 billion instructions per second), we can complete about 18 million instructions in 18 ms. As a result, with filesystems, we would like to minimize the amount of work the disk performs (overhead of seek time and rotational latency).
We'd like to measure how well our file system works, and to do that we need some metrics in order to gauge its efficacy.
In general things that are good at latency, are not good at throughput - the two are competing objectives, and you must make a tradeoff between the two.
Batching relies on grouping many small requests together, and executing them all at once. For example, if we have multiple small writes to perform, we can place them into a buffer and send them as one write once the buffer is full. The same concept can be applied to reads as well; if we have multiple read requests that are not urgent, we can wait for them to build up so that we can perform all the requests that read/write from similar locations in the disk all at once. This reduces the amount of time we spend waiting for the disk to seek/rotate.
One example is the cat program, which reads from STDIN and writes to STDOUT. The pseudocode is as follows.
1 while ((c = getchar()) != EOF)
2 putchar(c)
The function getchar() consists of a read (from the STDIN buffer, to your own buffer buf) and a write (to the STDOUT buffer):
1 read(0, buf, 4086)
2 write(1)
Notice that the read the function calls reads 4096 bytes, instead of just one. This is an example of speculation. In fact, according to Professor Eggert, batching is just a more specific approach to the concept of speculation.
Speculation allows the system to "speculate" on what will happen next in the program. In the cat example, instead of reading a single character each time putchar() is called, the system will read a bunch of data from the file, and speculate that the next character to be read will be in the same chunk of data already read. This is called prefetching - where we do work before we need it.
Conversely, the write version of prefetching is called dallying. Instead of immediately writing a character when putchar() is called, the system can wait until multiple putchar() calls are made, and make a single write at once, instead of carrying out calls as they are made.
The reason that batching and speculation work so well is locality of reference, of which there are two flavors.
In addition to the improvements described above, there are further performance gains to be made when considering the block layer.
Recall that the block layer is a primitive view of the file system that does not consider the fancy data structures that comprise the file system such as inodes, bitmaps, or boot sectors. Instead, it simply considers the disk to be separated into individual blocks (for argument's sake, 8KiB), and interfaces with the file system through simple instructions, like read_block(block_no) or write_block(block_no).
In this layer, we can model disk access by considering the disk to be a long array of blocks, and the disk arm to be a pointer to one of the blocks. Seek time is proportional to the distance between the current location of the read head and the location of the read request, so we can model the average seek time with the following integral:
In this equation, we consider 0 and 1 to be the beginning and end of the disk, with blocks equally spaced between them. h is the current position of the read head, and disk access requests are at random positions between the beginning and end of the disk. The seek distance is the difference between the location of the request and the location of the read head. As a result, arbitrarily fulfilling each request we receive in order results in, on average, traversing 1/3 of the disk. Because this seek time is slow and is the limiting factor to disk access, we minimize the disk traversal using disk scheduling algorithms to decide the order to process requests.
Also, in the equation's model we assume we receive random requests that are processed one at a time. However, in the block layer, we maintain a queue that holds all current disk access requests. In addition, requests are generally not random, and exhibit locality of reference (are clustered together). These two facts allow us to use scheduling algorithms for more efficient request processing.
This is a simple algorithm that seeks (haha) to maximize throughput by serving requests that are the closest to the current position of the disk arm. This minimizes our seek time, and increases both utilization and throughput. However, the problem with SSTF is starvation. If numerous requests for disk access are made on one side of the disk, a single request for disk access on the opposite side of the disk will never be served, and will starve. This is a nightmare for latency.
This algorithm is analogous to how elevators work. The disk arm will move right along the disk, serving requests that it passes over, until it reaches the rightmost request. Then, it turns around and moves left, serving requests along the way until reaching the leftmost request. This algorithm solves the issue of starvation, as the request on the far side of the disk is still guaranteed to be served, but it is still not a fully fair algorithm. Requests made on either side of the disk can only be served as the disk arm is moving in their direction. However, requests made closer to the middle of the block can be served as the disk arm is moving in either direction towards another request on the end. Therefore, the latency for requests in the center of the disk will be significantly lower than those on the edges.
This is a variation of the elevator algorithm where the disk arm only seeks in one direction, left to right. When it reaches the right end of the disk drive, the arm resets to the left end, and seeks again. This algorithm solves both starvation and fairness, but gives up some performance as we incur overhead when resetting the read head to the left end of the disk.
We weight each request as a function of how long it's been waiting and its distance from the disk arm (wait time - |location - head|). As a request spends longer waiting, its score goes up and its priority goes up. However, this is counterbalanced by its distance from the read head. As the request is closer to the read head, its score also goes up. This way, we find a balance between fairness and efficiency.
When the block layer implements one of these Disk I/O scheduling algorithms, the file system does not see the underlying workings. These details are invisible to the file system, and the file system only sees the performance gains of the scheduling.
Consider the simple system call to rename the file "foo" to "fuzzy":
1 rename("foo", "fuzzy")
This system call works as follows:
But wait, what if the directory entry is completely full when holding "foo"? Then there is no room for the extra two characters in "fuzzy", and we must grow the directory. To do so, the process of renaming gets more complex:
In total, we update four blocks: the directory inode, the original block for the directory entry, the new block for the directory entry, and the free block bitmap. It is important to note that we have to write these blocks in a particular order so that our file system does not accidentally leak free blocks, or worse, delete user data.
The safest order of writes is as follows:
The problem that occurs when we crash between 3 and 4 is the following: If we have 2 hard links to the same file, the link count is not updated, and remains 1. We didn't bother to update it, since we were just doing a rename. But when the user finds both hard links, and deletes one of them, the link count becomes 0, and the system reclaims the data blocks of the file, causing user data loss (this is the end of the world). To solve this, we actually have to update the link count in foo's inode from 1 to 2 before doing any of these dangerous writes, and bring it back down to 1 after they complete. In the case that the system crashes, we don't lose user data, we only have a free space leak, which isn't quite as bad.
When maintaining, writing, or using a file system, it is necessary to keep track of important properties of the disk. File system invariants are statements that will always be true even if we crash (assertions that should always be true)
BSD File System Invariants:
Consequences of violating the above invariants:
As we have seen, there are many avenues for data leak in the event of a system crash. In order to fix data leaks and reclaim unlabeled data blocks, we use the fsck (File System Checker) program. It bypasses all file system constructs and writes directly to disk in order to avoid the protections of the file system.
fsck finds:
In the first case, fsck simply corrects the leak by appropriately setting the free block bitmap. In the second, fsck takes the orphaned files and places them in the /usr/lost+found/ directory. As there are no parent directories for these files, the file names are lost. Instead, fsck uses the inode numbers for these files as the filenames, and waits for user to take action. Finally, permissions of these files are set to root, as they may have been lost when the files were orphaned.
Although the file system code reads and writes blocks in a safe order, the block layer does not respect any of these requirements. All reads and writes have no order guarantee at the block layer, so although the file system carefully dictates the order in which writes must occur, the block layer is free to (and probably will) write in any order to increase performance.
If our code crashes after the final unlink, before the exit() call, then both the last write to foo.gz and unlink() will be in the block layer’s request queue. These two requests can be served in any order by the block layer, and in the case that the unlink is written, followed by a crash, foo.gz will be deleted (since it’s not complete), and foo will be unlinked. This results in total data loss.
In order to work around this, the file system can be configured with the "ordered mount" option, which will insist that the block layer not use the request queue, and instead serve requests in a strict FCFS order.
Alternatively, the code can be modified by adding the following code after each write:
1 if (fsync(ofd) != 0) //this function call insists that the
2 error() //write to ofd be completed before moving on
The tradeoff with either of these solutions is that it is slow. Very slow. We trade a lot performance for consistency. But that is the cost of maintaining user data. This fix has already been implemented in the gzip source code.
In fact, this bug is so pervasive that it affects all sorts of applications across all operating systems.