Lecture 8 (02/03/2016)

Scheduling & Synchronization

by Eugene Liu, Brandon Liu, and Jennifer Liaw

Contents

Introduction

Last time...

In the last lecture, we talked about scheduling mechanisms; that is, how to switch from one thread to another. With scheduling mechanisms covered, it is now possible to discuss scheduling policy. Assuming we have the mechanisms working, scheduling policy is the high level idea of what we should do with the powerful mechanisms we built.

An Analogy

To introduce the topic of scheduling, consider an order for 500 Model T's from Chicago. Once this order is processed, we can start assembling these cars. We can start building cars, and after some time we complete our first car. Eventually more and more Model T's are being completed, but there is a very high demand for Model A's, so we switch to producing these cars instead. Sometime along the way, we'll switch back, finish our order of 500 Model T's, and continue to process new orders.

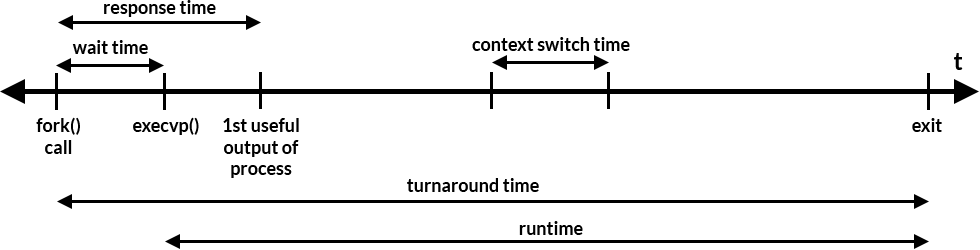
In a way, this is much like scheduling algorithms for computers. When an order first comes in, it's equivalent to a process being forked to run a job. An execvp() call can be seen as when assembly of a Model T begins. When the first car is completed, that is the first useful output of a process. Switching between making different cars would be a context switch. The turnaround time would be the time between the fork() call and exit, and runtime would be the time between execvp() and exit.

Program Schedule

First Come First Serve

A dumb, simple scheduling policy.

Suppose we are back in elementary school. The golden rule that was used to attend to students was very simple and very fair. Everybody takes their turn, and you take your turn in the order you arrived. The first student to arrive is the first student served. This policy is known as First Come First Serve (FCFS).

Let's have an example problem. Assume we have a system with four tasks: A, B, C, D. These tasks have the following characteristics:

Job Arrival Time Run Time Time to first output
A 0 5 0
B 1 2 4
C 2 9 5
D 3 4 13

"Job" is the job to be run. "Arrival time" is the time, starting at 0, in which each job arrives. "Run time" is the time it takes for a job to run to completion. Lastly, "time to first output" is the time it takes from when the job arrives to when it first starts outputting.

Time 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
Process Running A A A A A|B B|C C C C C C C C C|D D D D

A arrives and runs for 5 seconds. By the time A is done, B, C, and D are all waiting to run. We run B. This continues until D finishes. The time taken to run the jobs individually totals to be 20 seconds. Furthermore, we must account for context switches (denoted by '|') between threads, which we give a time of δ. Thus, the total time from start to finish would be 20 + 3δ seconds.

A few metrics can be used to compare different policies. Utilization measures how well the scheduler utilizes its time. This can be calculated by dividing the total time spent doing work by the total time from start to finish. In this case, it is 20 seconds / (20+3δ seconds) which should be a high number if δ is small.

Another metric that can be used is average wait time, which is the average of the time between when a job arrives, and the time until it start running.

The wait time for process A is 0 because it arrives at time 0 and starts at time 0.
B arrives time 1 and starts at time 5+delta, for a wait time of 4+δ.
C arrives at time 2, starts at 7+2δ, for a wait time of 5+2δ.
Lastly, D arrives at time 3, starts at 16+3δ, for a wait time of 13+3δ
The average of these times is just the sum divided by the number, which is ( 0 + (4+δ) + (5+2δ) + (13+3δ) ) / 4 = 5.5+1.5δ

Process Arrival time Start time Wait time
A 0 0 0
B 1 5 + δ 4 + δ
C 2 7 + 2δ 5 + 2δ
D 3 16 + 3δ 13 + 3δ
Average 5 + 1.5δ

From the point of view of throughput, utilization was not bad, since there were only 3 context switches between 4 jobs. This is the smallest number possible if we want to run every job. The wait time is quite long though, especially since job C runs for a long time before D can start.

Shortest Job First

Another scheduling policy

First come first serve had high utilization time, but an average average wait time. If our goal is to minimize wait time, we could try another scheduling policy. This scheduling policy is known as shortest job first, and it is exactly how it sounds: run the shortest job first.

In this case, jobs are not run in the order they arrive. At any given point in time, when deciding what job to run next, we pick the one with the shortest run time. Note that a job still must run fully to completion before another job is scheduled.

If we apply shortest job first to it, the schedule initially looks the same because when at the start only job A is available. At end of A, everything has already arrived. Since B is the shortest it is run next. Now, D is scheduled because it has a shorter runtime than C.

Time 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
Process Running A A A A A|B B|D D D D|C C C C C C C C C

With only three context switches the utilization is the same. But, the wait times will be different.

Process Wait time
A 0
B 4 + δ
C 9 + 3δ
D 4 + 2δ
Average 4.25 + 1.5δ

A few important things to note about shortest job first is that we must assume we know how long each job is. This is reasonable if we run our program in a well controlled environment. With this scheduling policy, though, we run the risk of starvation, which means that a job may never run. Since an infinite number of shorter jobs can keep arriving, there is no upper bound for the time a long(er) job may have to wait.

Shortest job first is not a fair scheduling policy, as it may have a longer process wait for an extended period of time to make way for shorter processes. First come first serve on the other hand is fair, since each process will run in the order it arrives, and won't have anything else scheduled before it.

Preemptive Scheduling Policies

Suppose our program is running fine until we get a massive job, longer than job C. Once it starts running, it will hold up the wait queue for a long time.

One solution is to use preemption, which context switches from one running process to another, even if it is still running. This solves the problem of a system that gets tied up doing one really big job.

The simplest preemptive scheduling policy is called Round Robin. Round Robin is like first come first serve but with preemption. It preempts each time a new job arrives, and runs each process for one unit of time before switching to the next shortest job.

Time 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
Process Running A|B|C|D|A|B|C|D|A|C|D|A|C|D|A|C C C C C
          ^B done   ^D done ^A done

If we do Round Robin, we hurt utilization because we spend much more time doing context switches. A quick calculation gives 20/(20+15δ) due to 15 context switches.

However, our average wait time is (0 + δ + 2δ + 3δ) / 4 = 1.5δ, which is really good!

This is even fairer than first come first serve because every process gets a chance to run. In this case, if a tiny little job comes in, you get that tiny little job done and then continue back to your bigger jobs.

There is an issue though, since you can still starve if a lot of small jobs come in, since they get sent to the front of the queue. Placing new jobs at the end of the scheduled queue is a remedy to this. If thought of like a lay-up line, each job gets a turn to run. Even if a lot of short jobs arrive, there will only be a finite amount before every job gets its turn.

Synchronization

Synchronization is the coordination of actions in a shared address space. Its goal is to maintain data consistency, which must be done efficiently, clearly, simply, and flexibly.

Race conditions occur between threads when they try to load and store from the same location in RAM since the default behavior is unsynchronized. Computation will silently proceed without notifying the user of any issues, making it very dangerous. It's like selling people a bunch of cars without brakes and seatbelts and saying just go drive them!

This is one of the central problems in OS design. The reason it's such a problem is that the general computational model we use is stupidly simple, yet we love it because it runs so fast.

Goals:

  1. Robustness and consistency
    • Data should be represented in memory robustly and consistently. Even in a delicate operation, at a high level, you want to look at RAM and know what state it's in and what’s going on.
  2. Efficiency
    • It's easy to just run a program single-threaded and have no synchronization problem. In some cases, like on a dual-core CPU, it may be worth the efficiency cut to not deal with synchronization. However, if you have a 100 core CPU, you would be wasting resources by running just a single thread.
  3. Clarity, simplicity, flexibility - In that orthogonal manner.
    • Code should be easy to understand and maintain.

Issues occur when there are an overlapping set of variables when threads are in the same state. That is, when a set of variables are shared between threads, and the threads are using and/or modifying the variables at the same time, then there may be a problem.

There are three main tools we can use to avoid this situation:

Sequence Coordination

Sequence coordination can be thought of having actions done before-or-after. This just means that no two states can overlap. That is, if a thread is operating on a particular section, it is the only thread doing so. Thus, every change must be coordinated such that all changes must occur before or after a state.

Isolation

Isolation is as it sounds. Threads are operated in isolation such that they don't share variables. Threads can operate in parallel as long as they do not have any variables in common. In this case there won't be any race conditions, so it doesn't matter what each of these threads do.

Atomicity

Another mechanism that can be used is atomic action. An operation is atomic if it is fully executed, or not at all. All other threads that see such an operation should never see it halfway complete. This is useful because it prevents cases in which an operation is interrupted. For example, if an operation halts in the middle, some values will be set, but others aren't. Ensuring that either nothing happened or everything was completed is important so threads can know the proper values of variables.

Let's now introduce the notion of observability, which is what an observer can see.

One of the assumptions made is that the shared variables are visible. All values are visible and we can see that they have been operated on.

However, there may be some shared variables that are not always visible to other threads. If something is not visible, then it technically isn't a problem. However, if something is not visible, there is no way to know if it's right or wrong, so this behavior is buggy.

Serializibility

Suppose we question if our implementation is correct or not. We can assume our implementation is correct if all observable behavior can be justified by serial execution of the transitions. This means that an outcome is correct if its outcome is equal to the outcome of all transactions that occur sequentially, with no time overlap.

Let's have an example of a pretend bank account with $100. Dr. Eggert and his brother both have cards that allows for depositing. Let's also assume that there is a thread T1 which represents Dr. Eggert, and a thread T2 that represents his brother. Lastly, say there is a shared variable named balance.

We start with $100. Dr. Eggert deposits $50. His brother withdraws $20.

int balance = 10000; // cents

int deposit(int amount) {
   balance += amount;
}

int withdraw(int amount) {
   balance -= amount;
}

In this very simplistic case, we will ignore a multitude of errors that include and are not limited to not checking for negative numbers, not checking for overflow, and not checking to see if there's enough money left in one's balance.

The issue we are concerned about is that this code is buggy if multithreaded. There are a multitude of race conditions such as two withdraws at the same time, two deposits at the same time, and a deposit and a withdraw at the same time.

This is because  balance += amount  is not atomic. It is broken up into three steps: loading the balance into the register, adding the amount, and storing the result. If two reads occur at once, and one write occurs before the other, then the written amount won't be accurate. The standard idea to prevent this from happening and come to serializibility is to implement atomicity around the section of code that is not atomic.

Critical Sections

A critical section can be thought as a small region of code and to be executed atomically, even if the machine would not have it that way normally. This is a section of code in which at most 1 program counter should be executed on behalf of any particular object (which is our balance object in this case). If a box is placed around this critical section, and at most 1 thread executes our box, then it'll be safe. Technically, a box can be drawn around the entire program to make one big critical section, but then that defeats the purpose of multithreading.

Too many critical sections and your performance goes to pieces. Critical sections that are too small will lead to better performance, but there will still be race conditions. Thus, there is a Goldilocks principle for critical sections:

Goldilocks Principle