

Learning Fast Neural Network Emulators
for Physics-based Models
Radek Grzeszczuk, Demetri Terzopoulos, and Geoffrey Hinton
Department of Computer Science, University of Toronto
Animation through the numerical simulation of physics-based graphics models offers unsurpassed realism, but it can be computationally very demanding. This paper demonstrates the viability of replacing the numerical simulation of model dynamics with a dramatically more efficient alternative. In particular, we propose a radically different approach to creating physically realistic animation that exploits fast emulators implemented as neural networks, which we call NeuroAnimators. NeuroAnimators are automatically trained off-line to emulate the actions of physics-based models, by observing the models in action. We demonstrate NeuroAnimators that have learned the motion not only of simple passive and active dynamic models, but also of state-of-the-art physics-based models reported in the literature, including mechanical models of a swimming dolphin and a running human. Depending on the model, our approach yields physically faithful animation one or two orders of magnitude faster than the conventional, numerical simulation technique.
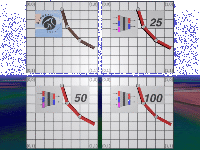
We employ the backpropagation algorithm [1] to train feedforward networks to efficiently predict the state transitions of the numerically simulated dynamical models. To gain additional efficiency, we train the networks to predict ``super timesteps'', one or two orders of magnitude larger than the timestep used for the competing (implicit) numerical simulator, thus accruing outstanding efficiency without serious loss of accuracy. Figures 1 and 2 show frames from animations that illustrate the technique for different non-trivial dynamical systems.



Figure 1: This plate illustrates the emulation of 3 different
dynamical systems: a three-link pendulum, an elastic cube and a
biomechanical dolphin. In each display, the physical model is
indicated by the Siggraph logo. In the third image the biomechanical
dolphin [2] is in the background.

Figure 2: Emulated motion produced by training a NeuroAnimator on state transition data generated by the numerically simulated (by SD-Fast) Hodgins mechanical runner model [3].