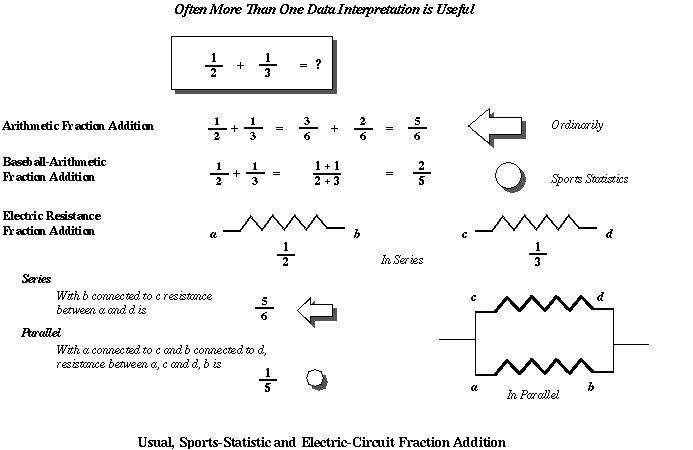
In the book [1] Kline looked at different ways for handling fractions. In baseball the usual way of computing batting averages defines a special kind of division. The baseball arithmetic operation is not the usual way we add fractions. But in electrical devices, their resistances add up differently depending on how they are configured. So in many ways how to calculate depends on the field: it is not an absolute. Here is a visual representation:

The book [2] takes the idea of field even farther, persuasively linking it with culture: it contains sophisticated examples of mathematical reasoning in tribal cultures (Australia, New Zealand, South Pacific, South America, and Africa). Both references [2, 3] present material about how mathematical concepts are embedded in aspects of life in places often thought of as backward. (See Africa or China.)
The Inca of Peru recorded number only via knots in cord. Yet as the excerpts from images in [3] show, they could build walls based on highly accurate fractional division of space.