Revisiting Cubes - Visual and Data
Structure Methods
by
Allen
Klinger and Paul Stelling
Abstract
Visual proof of
a proposition known to the early Greeks: The cube of every positive
integer is a sum of consecutive
odd integers. This proposition is shown to hold for all compound/non-prime
positive integers that are either odd or divisible by 4. For any such
number n, the unique smallest
such sequence has
size equal to the smallest prime factor of n. Finally, a
method for deriving the number of such sequences
for each n is given.Also, any
positive integer n that can be represented as a sum of consecutive
odd integers has a unique smallest sequence. The minimum number of consecutive
odds that sum to n is the smallest prime factor of n. Finally, an approach for deriving the number of
sequences of consecutive positive odd integers summing to n.
Introduction
In the first century A.D. one answer to the question ÒHow can the cubes be represented in terms of the natural numbers?Ó was given as follows:
|
First statement: |
ÒCubical numbers are always equal to the sum of successive odd numbers and can be represented this way.Ó |
This first statement paraphrases text[41]
which cites Nicomachus[52]. We
show here that structural concepts predominate over notation in enabling understanding
why first statement holds. The first two cases expressed in the usual way
show its meaning:
23 = 8 = 3 + 5 (1)
33 = 27 = 7 + 9 + 11 (2)
While the first statement strikes most people as unclear, (1) and (2) suffice to support a persuasive visual proof. However, further questions arise with the next larger integer. One representation of it is as follows:
43 = 64 = 13 + 15 + 17 + 19 (3)
In
addition there are the following
alternative representations:
43
= 64 = 31 + 33 (4a)
= 1 + 3 + 5 + 7 +
9 + 11 + 13 + 15 (4b)
These representations suggest questions about
the size and number of these sequences. The first visual
proof we show will prove the following
elaboration on the first statement:
|
Second
statement: |
ÒT |
Although
this second statement hints
atgives more of a clue
of how to
derive a sequence of consecutive odds summing to a cube, it does not provide a
method. Nor does it give real insight into the nature of the problem. For example,
how would 73 be decomposed as the sum of
consecutive odds? Are there
decompositions of size other than 7? Concise mathematical notation
enables terse representation of the value 343, but constrains thought. Visual
reasoning [31] can
be used to resolve the dilemma. One can see
what cube means and use it to
generate sums of consecutive odd decompositions
for the cube of 7, 12, 17, 25, or any other natural
number.
That the cube of any positive integer has a value that can be represented as the sum of two or more consecutive odd positive integers is easy to show visually. We begin by sketching how to do so for equations (1) and (2), and then show how to extend the respective approaches for all even and odd positive integers. The approach is fundamental, based on data structures, and applicable to the following more general questions:
á
Does cube
possess some special property? Does decomposition into consecutive odds hold
for other powers as well? What is the most general class of positive integers
that can be decomposed intoas the sum of
consecutive odds?
á We
have seen that for at least some valuesAre
there are more than one sequence of
consecutive odd integers summing to the value.
Under what circumstances is the sequence unique? When it is
a value unique? If not, what are the smallest
and largest sequences of such integers? For each value, how many such sequences
are there?[1]
The answers to these questions can be found easily using the visual proofs.
This paper consists of five sections. Section 1 presents a visual proof of the original problem. Section 2 simplifies that proof using tables. Extensions and generalizations follow in Section 3, which answers the questions posed above. Section 4 presents an arithmetic proof of the extended problem, while Section 5 summarizes our results.
First Statement - Visual Basis
Formally
For any positive
integer n > 1 the arithmetic cube n3 can be represented using a cube structure consisting of n«n«n blocks, each 1«1«1 in
size. This is, as
shown in Figure 1Figure
1:(12a)
and Figure 1Figure
1:(23a).
The cube has n layers of n2 blocks. These layers can be numbered 1
through n, beginning with the
bottom layer. Clearly, the number of blocks in each layer is even for even
n, odd otherwise.
If n is even then the two middle layers are numbered (n/2) and (n/2 + 1).
[E.g., if n = 2 then
these layers are numbered (2/2) = 1 and
(2/2 + 1) = 2.] Removing one1
block from layer (n/2 + 1)
and adding it to layer (n/2), as
shown in Figure 1Figure
1:(12b)Ð(12c),
results in two adjacent layers with consecutive odd numbers of blocks. For
values larger than 2, continue this process, removing (2i Ð 1) blocks from each layer (n/2 + i) and adding them to layer (n/2 + 1 Ð i) for each i from 2 to (n/2). Thus for n even, n3 is
the sum of the n consecutive odd
integers from (n2 Ð n + 1) to (n2 + n Ð 1), which can be verified by summing.
Similarly, if n is odd then the middle layer is numbered (n + 1)/2. [E.g., if n = 3 then the middle layer is numbered (3 + 1)/2 =
2.] Removing two blocks from the layer above it [(n + 1)/2 + 1 = (n + 3)/2] and adding them to the layer below
[(n + 1)/2 Ð 1 = (n Ð 1)/2] as in Figure
1Figure 1:(23b)Ð(23c),
gives three adjacent layers holding consecutive odd numbers of blocks. Continue
this, taking 2i blocks from each layer
[(n + 1)/2 + i] and adding them to layer [(n + 1)/2 Ð i], for i
= 2 to [(n Ð 1)/2].
Thus for n odd, n3 is again the sum of the consecutive odd
integers from (n2 Ð n + 1) to (n2 + n Ð 1). This also can be verified by
summing.
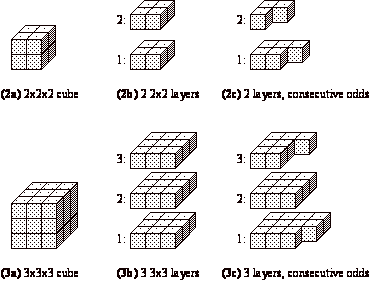
Figure 1. Base steps for cubes as sums of odd integers: n=2 and n=3.
Visually or Informally
Once the images
in Figure 1Figure
1
have been drawn, the decomposition process has two parts. The key observation
is that all positive integers are either odd or even.
For even n, the image based on n = 2 suffices. The horizontal plane between layers (n/2) = 1 and (n/2 + 1) = 2 symmetrically divides the layers of the cube. The layer immediately above the plane is decremented by one to obtain an odd value in the decomposition. The layer immediately below the plane is correspondingly incremented by one. The process continues, decreasing and increasing the adjacent layers by two more until all layers are exhausted.
When n is odd so is the
value n2 and
it is an element of the sum. I,
since it is the number of elements in the middle layer. The layer
immediately above is decremented by two, and the layer immediately below is
incremented by two to obtain the next smaller and larger odd values in the
decomposition. Analogous to the case for even n, the process continues, decreasing and increasing
the adjacent layers by two more until all layers are exhausted.
The visual proof reduces to observing that the Figure
1Figure 1
representations of equations (1) and (2), and similar representations for
larger n, correspond to data structures.
Further, these structures can be used to generate a sequence of consecutive odd
integers that sum to any required cube, as demonstrated just
as do the two shown in Figure 1Figure
1 for (1) and (2).
For any integer n these data structures
enable provide the basis for the algorithmic computation
required byderivation of values satisfying the first
statement.
Second Visual Proof
We
now note that the proof relies only on three facts:
á
Every layer initially has the
same number of blocks;
á
The number of blocks in each
layer has the same even/odd
parityor odd even
nature as the number of layers; and
á
The number of blocks in all
the layers combined equals is equal to the
sought total.
TheThis
proof does not use the fact that each layer is initially configured as [PFS1]a square. Representing each layer as a row is useful, since
it replaces the initial (threeÐdimensional) cube
by a simpler (twoÐdimensional) array.
The array consists of n rows with n2 blocks in each row. The number of blocks in
each row is odd if n is odd, and even
if n is even. The same approach to
moving blocks can be used as when the blocks were arranged in squares, as
illustrated in Figure 3Figure 2.
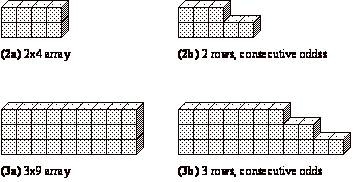
Figure 32. Illustration of
the simplified constructive visual proof using arrays for the even and odd base
cases that the cube of every integer > 1 can be represented as the sum of
consecutive odds.Simplified
representation of base cases
Note that this construction works for any positive integer n that can be represented as the product of two integers of
the same even/odd parity. I.e., let the integers be r (rows) and c
(columns), where r ² c and c and r are either both even or both odd. That is, begin with a
data structure as in Figure 3Figure 2:(12a)
[Figure 3Figure 2:(23a)],
and end with one like that shown in Figure 3Figure 2:(12b)
[Figure 3Figure 2:(23b)].
Clearly the construction applies for any positive compound
integer n that is either odd or
divisible by 4.
Suppose we have such an n. Then the smallest number of rows that can be used is the
smallest prime factor of n. It follows
that the smallest number of consecutive odds that sum to n is just the smallest prime factor of n. Similarly, the largest number of rows is the
largest factor f of n
that is smaller than 
and such that f
and n/f are either both
even or both odd. Thus the
largest number of consecutive odds that sum to n
is f as just defined.
It immediately follows that
every positive integer greater than one that can be represented as ki, where k > 1
and i ³ 2 are integers, can
be represented as the sum of consecutive odd integers. In this situation, we
can clearly use k rows and k(iÐ1)
columns. (This holds since k ² k(iÐ1),
and k(iÐ1) is even iff k is even.)
The question remains: For any given positive integer n, how many such sequences are there? Let 
be the number of
sequences of consecutive odd integers that sum to n. Based on the visual construction, it is easy to see that 
is the same as
the number of suitable rectangles that can be formed with n blocks. I.e., the number of rectangles where the number of rows and
columns are either both even or both odd, and where the number of rows is no
greater than the number in each row. Clearly, the number of rows must be a factor
of n. A factor of n is proper
if it is not 1 or n. Let 
be the number of
factors of n, and let 
be the number of
proper factors of n.
For odd n it must
hold that 
is the number of
proper factors of n that are 
. This number is 
. If n is even but
not divisible by 4, then 
. If n is divisible
by 4, then 
is the number of
factors of 
that are 
. This number is 
. Note that 
is even unless n is the square of an integer. Also,
is easily computed as the product of the exponents of the
prime factorization of 
. E.g., if the prime factorization of 
is
, then 
. For example, the value 64, the cube of 4 (64=43),
is both even and divisible by 4: 
. Hence, 64 can be represented as the sums of 
sequences of odd
numbers. These sequences are of length 2, 4, and 8, and appear above in (3).
An Arithmetic Proof
We assert that any composite positive integer n that is either odd or divisible by 4 can be represented as
the sum of consecutive positive odd integers. Further, there is such a sequence
of size p, where p is the smallest prime factor of n. This can be demonstrated by summing the consecutive odd
integers over an interval from 
to 
. That sum is given as:
(4)
By using (4) it is possible to derive the results given in
the previous sections, namely that:
n is the sum of
consecutive positive odd integers iff n
is either odd or divisible by 4, (5)
the smallest such sequence has length equal to the smallest
prime factor of n, and (6)
the number of such sequences is 
if n is odd, and 
if n is divisible by 4. (7)
However, the derivation is
beyond the scope of this paper, Moreover, it would be more complicated and
difficult to understand than the simple visual proof presented above.
Conclusions
We have demonstrated simple visual proofs that for any
integer n ³ 2, n3
can be represented as the sum of consecutive (positive) odd integers. The
extended visual proof based on array data structures led to further results.
They were visual and arithmetic proofs that this property not only holds for
all ni where i ³ 2, but for all composite positive integers that are
either odd or divisible by 4.
The value of the visual methods and their data structure
representations is evident because they enabled further extensions. We used
them to show two things. First, whenever n can be represented as a sum of consecutive (positive) odd integers, the
shortest such sequence of odd integers has length that isequal
to the smallest prime factor of n. Second, we showed how to get compute
the number of such sequences for any given n. These extensions were facilitated and made comprehensible by
insights gained using the visual representations.
We believe that data structures and visual representations
of mathematical concepts are essential tools. Our experiences have convinced us
that visual proofs lead to mathematical understanding. We hope that concepts we
presented will be used elsewhere. We believe the visual and data structures
approaches have value both for mathematicians and lay people. We welcome
further communication or discussion of the points raised here.
References
[1] Adams, James
L., Conceptual Blockbusting: A Guide to Better Ideas,
3rd ed.,
Addison-Wesley, Reading, Massachussetts, 1986.
[2]
Graham, Ronald, Donald Erwin Knuth, and Oren Patashnik, Concrete
Mathematics: A Foundation for Computer Science, Addison-Wesley, Reading, Massachusetts, 1988.
[3]
Knuth, Donald Erwin, The Art of
Computer Programming: Fundamental Algorithms (Vol. I),
Addison-Wesley, Reading, Massachusetts, 1968.
[4]
Naps, Thomas L., Introduction to Data Structures
and Algorithm Analysis,
2nd Edition, West Publishing Co., St. Paul, Minnesota, 1992, p. 50, prob. 4.
[5] Nicomachus, Introduction
Arithmetica, first
century A.D.
[1]
Naps, Thomas L., Introduction to Data Structures
and Algorithm Analysis, 2nd Edition,
West Publishing Co., St. Paul, Minnesota, 1992, p. 50, prob. 4.
[2]
Nicomachus, Introduction Arithmetica, first century
A.D. (see [1]).
[3]
Adams, James L., Conceptual Blockbusting: A Guide to Better Ideas, 3rd ed.,
Addison-Wesley, Reading, Massachussetts, 1986.
[4]
Knuth, Donald Erwin, The Art of Computer Programming: Fundamental Algorithms
(Vol. I),
Addison-Wesley, Reading, Massachusetts, 1968.
[5]
Graham, Ronald, Donald Erwin Knuth, and Oren Patashnik, Concrete Mathematics:
A Foundation for Computer Science,
Addison-Wesley, Reading, Massachusetts, 1988.