Words for Number Concepts
|
|
- Product
- Numerator
- Denominator
- Quotient
|
- Ratio
- Factor
- Prime Number
- Limit
|
|
|
|
Rational and Unit Fraction are other phrases that have different
meanings in today's mathematical context than in the past. Probability is the basis of
gambling and many games. Some
terms above are historic. They remain valid but awkward and
sometimes obstacles. The years
1991 and 2002 have special numbers. No other 20th century year
reads the same left to right and right to left.
Like years 1997 and 1939, 1991
is odd. But year 2002 is divisible by two, hence even. It possesses the
reversible quality, and so has
palindrome nature. 1991 and 2002 are
joined additively by the (odd) palindrome 11. Are there other such years possessing this property
with no palindrome between them?.
I know what a unit is but thought it very odd that this statement went
over my head a few years ago. You know of course that the Egyptians
used only unit fractions. - numbers via
hieroglyphics has more on this topic. But notice that the word
fraction was seen as ordinary or usually understood,
and not placed in the above table! So we need another set, terms
for K-12.
Although square, cube and exponent are well known concepts you may find
combining the following two facts with practical answers sought below
them oddly troubling and a poor fit with other number topics.
-
Every squared positive integer
can be represented as the sum of adjacent odd numbers.
-
Every cubed positive integer
can be represented as the sum of adjacent odd numbers.
- 92 = 81 = ?? (what sum of adjacent odd numbers)
- 73 = 343 = ?? (what sum of adjacent odd numbers)
The word factor could help someone trying to discuss in ordinary
words the elements of equations shown at solution. An easy-to-read description of factorial joining it with factor could help some
people. Reasons for the enormous
quantities from multiplying many
factors ... and how exclamation points ( ) convey a special notion could help.
) convey a special notion could help.
Finally, isn't it odd that a batter who hits once in three at bats in a
baseball game, and the next time has a single success in two tries doesn't
bat five-sixths? It depends on which arithmetic you use for
fraction addition. Two "unconventional" possibilities are baseball and electrical. But isn't it odd
that we think them unconventional?
Oddly enough we consider limits to be known only for a few hundred years
although the Greeks knew a great deal about their
use to determine circle areas. They used nested circles and both
described and evaluated a hard-to-compute nonzero limit1.
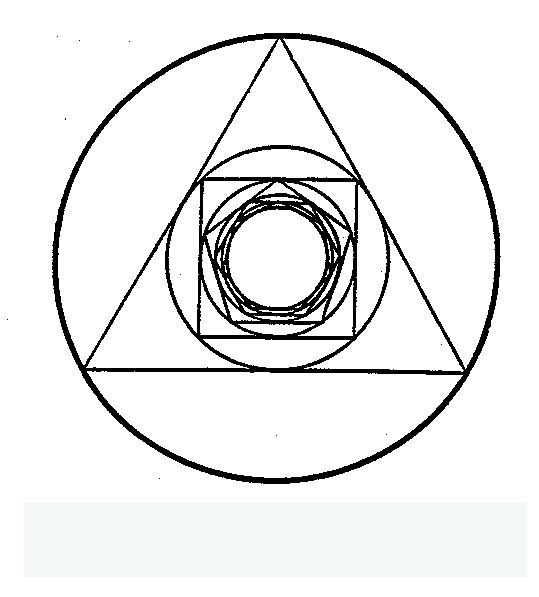
1Kasner and Newman,
Mathematics and the Imagination, NY: Simon and Schuster, 1940; ISBN
1-55615-104-7 Redmond: WA, Tempus Books of Microsoft Press, 1989, Fig.
125, p. 311.
| 4/4/06 Version |
|
http://www.cs.ucla.edu/~klinger/gnames.html |
|
|
|
©2006 Allen Klinger
|

