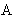Pattern Measure
Zhen Gu1
Introduction
Measuring Complexity in Visual Design Patterns with the Pattern Measurer.
There is no standard for comparing and contrasting patterns and images in computer science. The human eyes are good tools for distinguishing patterns but they cannot attribute a number to a certain image pattern. This section of the report discusses a method for assigning quantitative visual complexity to patterns and images and how this method can be used in the real world using a program called the Pattern Measurer.
Measuring Complexity in Visual Design Patterns
This study is based on Complexity and Visual Images proposed by Dr. Allen Klinger2 and Nikos A. Salingaros3. The idea is to use quantitative measures to a given pattern, such as Temperature (T), Harmony (H), Life (L) and Complexity (C) to distinguish between different complex patterns. I am using a program called the Pattern Measurer implemented by Trask Stalnaker4. I will demonstrate how to distinguish between two patterns using this notion of visual complexity. I will represent the symbols using different shades of color.
Symbol Representation:
| # | * | + | 0 |
| black | dark grey | light grey | white |
 |  |  |  |
Figure 1. Color representation of symbols.
Locally Imperfect and Symmetric Patterns:
+ + 0 0 * * + + 0 0 * *
+ + 0 0 * * + + 0 0 * *
# # # # # # # # # # # #
# # # # # # # # # # # #
* * 0 # + + * * 0 0 + +
* * + * + + * * 0 0 + +
Figure 2. Two sixteen-element arrays with symbol representation. (Klinger [1], p. 8)
The symbol arrays in figure 2 can be represented as color arrays using our symbol representation. This is shown in figure 3.
| Measure | Value | | Measure | Value |
| Temperature | 2.36 | | Temperature | 2.26 |
| Harmony | 0.87 | | Harmony | 1.86 |
| Life | 2.06 | | Life | 4.2 |
| Complexity | 19.15 | | Complexity | 16.09 |
Figure 3. Two sixteen-element arrays with color representation shown with their measures and values taken from the Pattern Measurer.
The two patterns in figure 3 differ only in three elements and the differences in their measures are as follow:
| Measure | Change in percentage |
| Temperature: | -4.24% |
| Harmony: | +114% |
| Life: | -104% |
| Complexity: | -16.0% |
Table 1.
I conclude from the data that pattern one is much less complex than pattern one. The values for temperature were fairly constant. For harmony and life, the values of the second pattern more than doubles that of the first. Overall, the second pattern is 16% less complex than the first pattern. It is easy to tell, by merely looking, that pattern two is simpler than pattern 1 because the lower center subblock of the first pattern contain four different symbol while in pattern two, the corresponding subblock is uniform with only one distinct symbol. With this quantitative complexity system, I can put an actual number on how much more complex one pattern is compared to another.
Four Element Binary Arrays
| 1. | 2. | 3. | 4. |
| 0 0 | 1 0 | 0 1 | 1 0 |
| 0 0 | 0 0 | 1 0 | 1 1 |
 |  |  |  |
| Array 1 | Array 2 | Array 3 | Array 4 |
| Measure | Value | Value | Value | Value |
| Temperature | 0.0 | 1.0 | 1.0 | 1.0 |
| Harmony | 0.6 | 1.0 | 3.0 | 1.0 |
| Life | 0.0 | 1.0 | 3.0 | 1.0 |
| Complexity | 0.0 | 8.0 | 6.0 | 8.0
|
Figure 4. Four four-element binary arrays shown with measures and corresponding values.
(Klinger [1], p. 3)
This is a good example to address the issue on similarity. Notice the array #2 and array #4 have the exact same complexity. This is because the color of the blocks does not matter, it is the difference between each subblock that matters. In the array #2, there is one black subblock and three white block. This, if disregarding color, is exactly the same as the array #4, where there is 1 white block and 3 black ones. If the one black block and the three white blocks are changed to one white block and three black blocks, respectively, arrays #2 and #4 will be mirror images of each other. This makes these 2 matrices similar.
Computer Graphics
In the field of Computer Graphics, the Raster Display Architecture uses 2-dimensional binary arrays as a refresh or frame buffer (Foley [2], p. 12). The screen is represented with a refresh buffer of 0s and 1s (Figure 5). Each pixel can be either on (have a binary value of 1) or off (have a binary value of 0). If a pixel is on, then the monitor will light and display that pixel, if its off, the monitor will display it as the background of the picture or black.
Raster-scan display is refreshed at a rate of 60 to 80 frames per second (Hearn [3], p.40). Using complexity description of each frame, we can calculate how complex a frame is and in turn calculate how fast it can be refreshed. Here the frame and the monitor screen is 16 pixels tall and 32 pixels wide and the refresh buffer is processed by the video controller and the simple image is displayed on the monitor as shown.
a) figure to be added.
b)
| Measure | Value |
| Temperature: | 0.36 |
| Harmony: | 6.48 |
| Life: | 2.34 |
| Complexity: | 0.91 |
Figure 5. a) Architecture of raster display. (Foley [2], p. 12) b) five hundred seventy six-element graphical representation of raster refresh buffer.
Quaternary Tree of Subblocks
Another way of analyzing an image pattern is by divide and conquer. This is done by dividing a big picture into smaller ones.

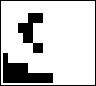
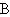
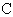

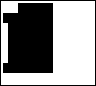
| | |
| Subblock A | Subblock B | Subblock C | Subblock D |
| Measure | Value | Value | Value | Value | Sum | Average |
| Temperature | 0.11 | 0.22 | 0.31 | 0.25 | 0.89 | 0.22 |
| Harmony | 8.25 | 7.69 | 7.39 | 7.64 | 30.97 | 7.74 |
| Life | 0.92 | 1.71 | 2.26 | 1.91 | 6.8 | 1.7 |
| Complexity | 0.08 | 0.29 | 0.49 | 0.34 | 1.2 | 0.3 |
Figure 6. Four divisions of a five hundred seventy six-element array.
I divided up the image from figure 5b into four equal one hundred forty four-element subblocks to study each subblock separately. According to the averages of all the measures, each subblock is less much less complex than the big block by itself. If I am to divide even further each subblock into four more subblocks, creating a third level for the quaternary tree in figure 7, I predict the smaller subblocks will be even less complex because there are less pixels in each subblock. The overall changes from the big picture to the average of the smaller pictures are show in the table 2.
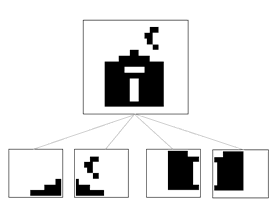
Figure 7. Quaternary Tree representation of subblocks.
| Measure | Change in percentage |
| Temperature: | -39% |
| Harmony: | +19% |
| Life: | -27% |
| Complexity: | -67% |
Table 2.
The harmony value is increasing and the other measures are all decreasing implying that the overall complexity is decreasing.
Another method for comparing the values is using ratios between each subblock value and the root value as each subblock's contribution to the whole (table 3).
| | |
| Measure (M) | MA/Root | MB/Root | MC/Root | MD/Root |
| Temperature | 0.31 | 0.61 | 0.86 | 0.69 |
| Harmony | 1.27 | 1.19 | 1.14 | 1.18 |
| Life | 0.39 | 0.73 | 0.97 | 0.82 |
| Complexity | 0.09 | 0.32 | 0.52 | 0.37 |
Table 3.
The Pattern Measurer
The Pattern Measurer program takes in an input pattern and outputs the Temperature, Harmony, Life and Complexity of that pattern. It can also calculate the temperature and harmony of that pattern with different dimensions. The pattern space where the images generated is also resizable. The user can choose how many elements for the width and height. The user can also specify the number of pixels for the width and height of each element in pixels.
Below are a few more snap shot of the patterns that are generated using this program including their temperature, harmony, life, complexity and also the temperature and harmony for different subblock dimensions using the same pattern.

| Measure | Value |
| Temperature: | 0.0 |
| Harmony: | 8.4 |
| Life: | 0.0 |
| Complexity: | 0.0 |
Data for different size arrays with the same patter:
| Subblock Dimension | Temperature | Harmony |
| 4 elements | 0.44 | 5.92 |
| 25 elements | 1.0 | 1.5 |
| 100 elements | 3.0 | 1.0 |
Figure 6. A one hundred picture element pattern consisting of four diagonal bands.

| Measure | Value |
| Temperature: | 0.41 |
| Harmony: | 5.39 |
| Life: | 2.19 |
| Complexity: | 1.47 |
| Subblock Dimension | Temperature | Harmony |
| 4 elements | 0.04 | 8.81 |
| 16 elements | 0.7 | 8.42 |
| 100 elements | 0.19 | 8.24 |
| 400 elements | 0.36 | 7.4 |
| 625 elements | 0.5 | 4.5 |
| 2500 elements | 1.0 | 0.0 |
| 10000 elements | 1.0 | 0.0 |
Figure 7. The number three. A ten thousand-element pattern.
Figure 7 demonstrates the use of the pattern measurer in analyzing realistic images.

| Measure | Value |
| Temperature: | 0.69 |
| Harmony: | 6.14 |
| Life: | 4.23 |
| Complexity: | 1.96 |
| Subblock Dimension | Temperature | Harmony |
| 4 elements | 0.0 | 9.0 |
| 16 elements | 0.44 | 6.72 |
| 25 elements | 0.0 | 9.0 |
| 100 elements | 0.0 | 6.0 |
| 400 elements | 3.0 | 0.0 |
Figure 8. A four hundred-element pattern with four distinctly colored subblocks.

| Measure | Value |
| Temperature: | 1.25 |
| Harmony: | 2.99 |
| Life: | 3.75 |
| Complexity: | 7.55 |
| Subblock Dimension | Temperature | Harmony |
| 4 elements | 1.14 | 3.08 |
| 25 elements | 1.13 | 5.38 |
| 100 elements | 1.5 | 0.5 |
Figure 9. A flag design. Two hundred-element pattern.
URLs for the Pattern Measurer
The Pattern Measurer application can be downloaded at in zip format:
Pattern.zip
The Pattern Measurer can be accessed at:
Pattern Measurer
All of the sample image patterns use in this report can be downloaded at:
Images Directory
Conclusion
The Pattern Measurer can be used to assign quantitative values to design images. Its use ranges from pattern comparison tocalculation of screen refresh rates in computer graphics.
References
[1] Klinger, A., Salingaros, N. A., Complexity and Visual Images.
[2] Foley, J. D., Computer Graphics, Principles and Practice, pp. 11-12, 1992.
[3] Hearn, D., Baker, M. P., Computer Graphics, p. 40, 1997.
1 Zhen Gu, Undergraduate of Computer Science Department, UCLA School of Engineering and Applied Science, Los Angeles, CA 90095.
2 Allen Klinger, Computer Science Department, UCLA School of Engineering and Applied Science, Los Angeles, CA 90095-1596.
3 Nikos A. Salingaros, Division of Mathematics, University of Texas at San Antonio, San Antonio, TX 79249.
4 Trask Stalnaker, Department of Mathematics, UCLA.