Ellipses

Curves

Allen Klinger, © 11/21/2010
The lune in the night sky is made up of two curves. A replica can be seen in the figure that was composed in Microsoft Word from two overlapping circles.

Circles, squares, and triangles are some basic forms. To understand the movement of bodies in the night sky, people gave names like cube to related ideas. Some of those ideas deal with number and others with shape. Here are two:

An ordinary, counting, whole or round (not fraction) number, is said to be an integer.
The amount of space inside a closed line is known as its area.

Area for a square connects that shape to counting procedures; this is easiest to see if we ask how many squares with sides one unit fit inside a bigger square. A square is a shape in a flat surface like a piece of paper.

A cube is a shape in three space: the world, not a flat. People created games based on six-sided cubes called dice. One die is a single member of a pair of dice. The placement of dots on each face of cubes lets people see whether the up side has one-dot or some other number up to six.

Circles are not the only curve that is useful in understanding the night sky. If a circle becomes a flatter and longer curve, it describes how bodies like planets move around, or orbit stars. The word for this curve is ellipse. To see more about ellipses and orbits go to Ellipses and Planetary Motion (describing the contribution of Kepler). For a general description of terms focal point, vertex in an ellipse go to Worsley School, Alberta, CANADA or Wikipedia articles.

Johan Kepler, 1571-1630 established that planets move in an ellipse - they orbit the sun following curves like those below. He published three laws of planetary motion (1609, 1619).

The ellipse is a curve like a circle. The ellipse has two foci; they become the same single point in a circle. That point is the center of a circle.

The shapes below all are ellipses. The outer ones are circles, ellipses whose two focal points overlap at the center. Another word, vertex, describes end or extreme points of these curved shapes.

Ellipses:

Same focal points.

Same vertices.

Total distance between any point on an ellipse curve and the two focal points is a constant: same sum for both lengths regardless of chosen boundary point.

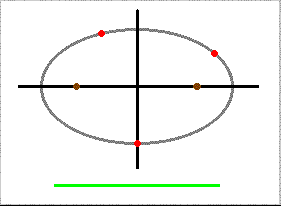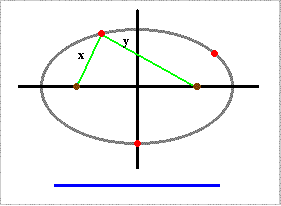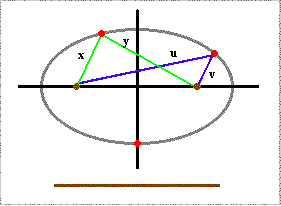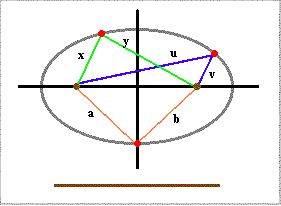
x + y = u + v = a + b = constant

For a circle the two focal points coincide - they are both at the center. The circle center-to-curve distance is the radius. It is the same for all boundary points.

	11/21/10 Version			http://www.cs.ucla.edu/~klinger/nmath/ellipse.html
	©2010 Allen Klinger