This page supports trying new starts in math learning. That people can do
math but think they can't, makes many unable to work with technical
devices (e.g., computers).
Daily life uses numbers like twenty-four, twelve, sixty and three
hundred sixty. Looking at them as in
hours in a day (24), or examining the number of eggs in a cardboard carton (12, a
dozen), minutes in an hour (60), and degrees in a complete rotation (360),
can build numerical capabilities.
People often do things that have math background. They play card
games, are active in sports, gamble, make health decisions, and do many other
practical things (like buying insurance) that involve mathematics.
Items posted here could help kindle interest in starting math again.
That is, learning in a less formal way.
Need for mathematical knowledge happens. That tells us we need
learning activities in mathematics.
A rough idea of how to start such an activity begins in a
recent paper[15] latest version. Large numbers of topics and the cultures that
gave rise to them appear at
St. Andrews Math History Topics. The geometric questions that arise
in an ancient puzzle are another possible start point.
There are many questions, I've considered:
e.g., how to make an accurate approximation to one or another irrational number.
For instance, to see how to do that for the base of natural logarithms
got to e by powers.
Suppose you want to get started growing math capability. It could help if
you were able to tell when some statement is plain wrong. Even when
you're not sure which of two others is right, labeling the one that is
wrong should get some credit. To do that use two diagrams reachable from
clicking the link try.
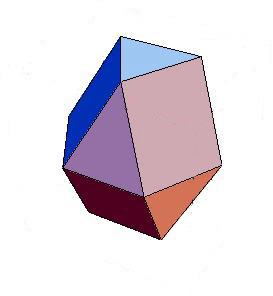
The diagram on the left is in color. It shows six differently-shaded colored (blue, red and rose), three- (triangular) and four-sided (rectangular) regions.
 |
solid_w_8_triangles
The middle of the diagram at left has six corners; its shape and name follow |  |
The Cuboctahedron is a very similar solid that was known to Archimedes. Like the image here it has "fourteen bases ... eight triangles". Instead of the Cuboctahedron's "six squares" the solid shown has that number of rectangles.
We could ask questions about these solids. In the image reached by the following link,
try, the right
diagram is black and white, with two kinds
of lines, solid and dashed. The labeled points are each
assigned
one of the thirteen
letters from a to m. The purpose is to allow a person to reflect what he or
she believes regarding three simple statements characterizing a situation (like these
solids).
If the light blue and light red regions were moved they and the light
rose shape could make a six sided planar (lying in a flat plane) shape.
Let's call the statement "Left figure has a six sided shape" the a label. (It is wrong, but if movement
were allowed it could be right.) Let's call the statement "There are only
triangular or three-sided and rectangular or four-sided regions in the
colored part of the two diagrams," the b label. If c stands for "All the
regions are three-sided in the colored part of the two diagrams," we know
that is wrong but some people might not realize that.
Any answer on a line touching b (the correct answer) should
get some credit. Any answer on a line between the two incorrect answers
a and c should get nothing. Finally an answer of "I don't
know," m should be rewarded somewhat (for honesty).
Links tagged with * show untraditional sources. Many are like this dancer:
 they move (are animated). Some speak. Others jump between topics
or are
unconventional
beginnings. All
could be part of
offering new
entry points to
math.
They are
prototypes for
using the
world-wide web
to enable
re-entering the ideas of mathematics.
they move (are animated). Some speak. Others jump between topics
or are
unconventional
beginnings. All
could be part of
offering new
entry points to
math.
They are
prototypes for
using the
world-wide web
to enable
re-entering the ideas of mathematics.
Italic links go to new items I've written. Other links are to student activities I've led. Others are things I've found on the web that could be worked into new K-12 class activities.
Starting |
Read |
Night Sky* |
Words |
Sizes* |
Math Site |
Girls |
Questions |
Culture |
Associate |
Islamic Mathematics |
Ten |
Puzzling |
Ancient, Origins (Babylonian) |
Sounds/Visuals |
Listen | Probability* | Multiply* | Nested Graphic* | Nested Analytic* | Pi and More*[26] |
Numerals |
Sequences[8] |
Numbers |
Recent |
Special[25] |
Smith |
Structure |
Computer Sources |
GAP[6] |
Ways to Number |
Binary* |
Area*[4] |
Symbols/Images | Projects |
Math Sources |
Algorithms[3] |
World[2] |
Curves[6] |
Sphere's Insides*[16, 17] |
China[13] |
Induction |
Games |
Seeds | Mancala |
Laskers* |
Cards* |
Squares* |
Spatial[27] |
People/Problems |
Sonia | Easy?* | Collatz Problem[2] |
Collatz Paper[5] |
Make Change[14] |
Make Change Solution[14a] |
Math Reference |
Interactive Math |
Sum Integers' Powers[7] |
Quotition |
Surfaces |
Modern Mathematics |
|
Counting |
Tally |
China's |
About Nine[13] |
Averaging |
| Right Triangle | Triangles in Space | Round - Ellipse | Repeat - Recursion |
Visually | Sum Squares | Sum Squares By Three |
| 03/13/2014 Version | http://www.cs.ucla.edu/~klinger/nmath/index2.html | ||||||
| ©2011 Allen Klinger |