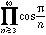
This paper includes contributions by M. Chatterji, A. Menhenett, D. Delsol, S. Patel, D. Tham, S. Farivar, M. Arora, A. Crow, M. McNally, E. Landaw, and W. Wei; S. Cheng, J. Ou-yang, N. Paris, Q. Nguyen, T. Toyoaki, D. Ramji, K. Yeh, and J. Donnelly participated in discussions while E. Ensafi and W. Lushbaugh also supported the reported activities.

Introduction

This item sums up what we did, and to some extent why we did it, in an undergraduate course entitled Computer Science Design Project. There are at least two main components to this. First, to convey how a straightforward challenge fosters learning, and how that took place without a preconceived agenda based on past achievements in a field of work. Second, to describe how the undertaken activities supported the general course goals, and to highlight their role in developing a vital undergraduate learning experience. Most significantly, almost all contributors to this note are undergraduate students. The work reported here really was done either by the class as a group, or by individuals reacting to questions or topics mentioned to stimulate learning.

At this university, as in many major research campuses, most courses available to undergraduates are large and impersonal. This term the design project course definitely was neither. The course was successfully completed by sixteen students working in five teams. Since many students work late into the night, frequently few people were present at the eight-in-the-morning start time. Unplanned exchanges with those there, and the instructor's own interests, led to topics that supplemented student design projects and enlivened the course.

The course evolved guided by student interests within the primary and secondary overall goals, namely above-all, creating teamwork, while building strength at making presentations, composing visuals, and preparing reports. Within the first few weeks, we began discussing two main areas. The first is the value of π as a continuing series of digits. The second is another irrational that arises geometrically and can be expressed analytically as an infinite product. The product expresses the limit of a circle radius, as more and more inscribed polygons, and inscribed circles within them, nest within the original unit-radius circle. (Successive polygons have increasingly-many numbers of sides, and hence get closer to their circumscribing circle.) We stressed the ethical issue of proper attribution and focussed our work on improving students' overall exposition skill and strenghtening their group interactions. While the mathematical areas provided illustrative examples, they had another consequence.

The above two activities caused added effort by many class members. Their individual initiatives created a stimulating work atmosphere that furthered the way we all learned this term. Frequently they initiated computer-search activity that located enriching programs and resources on the internet. Their actions represent both the contributors' skills and UCLA's high-quality environment: computing facilities, libraries and research mission.

Learning From Others

This paper describes project course activities to involve participants in working with, and learning from, others. This can be planned only with sacrifice to spontaneity and interests. The approach taken was to establish a system to ensure that this occurred, but to allow a wide range of class presentations and discussions. The only two requirements were that presentations either focussed on an aspect of a student's project, or portrayed something visually. Only in the latter case were the talks scored, and a rating obtained from the votes of students who listened to (and watched) the speaker.

This approach places much reponsibility on the students. Nevertheless, good intentions are enforced by system rules: grades, schedules, class deadlines, and office hours,. When students failed to come to class, or arrived late, informal discussions with those present started the things reported here. I initiated discussions from topics that interested me and used them as illustrations of general course objectives. They helped portray: 1) how visuals facilitate exposition; 2) how to apportion emphasis between pictorial, written, and verbal presentation methods; 3) techniques to sustain within-group communication; and 4) methods for building a cooperative team effort.

Some of my discussions began with e, the base of natural logarithms, others with p, and some with properties of the natural numbers. Illustrations of using the catenary in architecture led to discussion of cosh, the hyperbolic cosine, and power series. That led a subsequent class meeting into an inquiry about the relation of the hyperbolic and circular (sine/cosine/...) functions. In all this I freely asked questions, including ones where I had no idea of the answer. [Such questions invariably got me into the library to do research after class. Similarly, they led one student into the bookstore for the same purpose: he worked with more recent books.] Quite often I employed words, abbreviations, poems, games, or humorous visuals. Most discussions triggered outside activity in some course participants. Sometimes the activities led to totally unforeseen events, such as: 1) locating individuals' birthdates in π ; 2) evaluating billions of iterations of products of cosines; 3) exploring research questions about the limit of the cosine product; and 4) learning about mathematics and history. In all cases the relation to the course was initially completely unplanned. Still, these unplanned activities frequently became very useful tools in highlighting and accomplishing the underlying purposes of the course.

A class submission assignment showed the way composing a visual (as a homework item) fostered learning. Students' creativity and initiative led to many items including, Visual Computing where this statement appears. "A visualization of the first 1.5 million digits of PI ... image ... produced using two BCD encoded digits to make each byte of an RGB triplet". The item is a full color image. It is best seen at Graphics Research. The work is that of the following Simon Fraser University Faculty: Tom Calvert, John Dill, David Fracchia, Wo-Shun Luk, and Thomas C. Shermer.

The Project Idea and its Relationship to Learning about Mathematics

The UCLA Computer Science Design Project course supplies students with two things. First, the opportunity to define or select a project. Second, involvement in a presentation/reaction process. Student presentations given early in the course help recruit the project group: people to work on a commonly-agreed project. The course has only three minimal requirements. Students must present their project idea to their classmates at least twice during the ten week quarter. Generally these talks stimulate further work, expose choices to constructive criticism, etc. Students must show that they are active participants by comments on others' presentations. Each student has to be part of a team that completes a draft project report, and turns in a final report before an established deadline.

The above requirements are technically minimal yet actually rather demanding. The first demand is that students learn to work together in a team for a mutually-established goal. Second, each step toward that goal requires public speaking, preparing visual aides, composing report figures (graphs, charts), and writing lucid text. Public speaking is difficult and requires preparation. Moreover, everyone fears having to speak in public. The result is that the course is filled with personal challenges. The challenges are more difficult because there is no pre-established topic, instead it is a matter of students' choices, preferences, and judgments. The lack of a preassigned formula to execute in planning a talk puts a burden on both the speaker and the audience. It forces the speaker to deal with plans, goals, and choices. The audience must interact with the speaker: the students have to engage with the actual presentation, something they cannot prepare in advance. The most successful students integrate decisions about their project into their talks. Still, for all participants, the speaking requirement helps by creating learning, or stimulating refining, of skills that contribute to success in the workplace.

Learning and acquiring skill requires one to try something new, practice, and improve. The course strives to create self-awareness, to strengthen students' ability to criticize and revise written, visual, and talk materials. The breadth and variety of mathematical concepts ensures that someone will find something presented to be novel. Likewise, there often will be someone having special knowledge or interest in a mathematical topic. Even more interestingly, for computer science students the stimulus of a mathematical question points them to the available computing power. Many have little acquaintance with modern computer-based math-tools: Mathematica, Maple, MatLab or mathematical reference books such as the Handbook of Mathematical Functions [1].

The diversity of mathematics coupled with past numerical work (as in [1]) and the wide variety of powerful contemporary computational systems, supports adding unconventional analytical topics to the design course. For one thing, they provide a neutral domain for discussing exposition, in place of speaking about a current or recent-past project. For another, while the students have seen many standard mathematical expressions involving S for summation and P for product, they rarely encounter the limits of the power of their own computing resources. The resources range from hand-calculators, to personal computers, and to large computer systems. Still, evaluating actual S and P expressions is infrequently required of university students. Finally, throwing students a difficult computational issue is a well-established computing tradition. The long-unsolved problem of whether applying the rule if even divide by two, if odd triple and add one leads to a cycle from any positive integer other than one, is not likely to soon yield a result [2].

Furthermore, using mathematical topics increases the students interest in the subject, presents insights that may be useful for future engineering work, encourages them to use their skills at writing efficient computer programs, and stimulates conducting computer searchs using the internet.

Topics and Management

The course involves participation, especially in a team project. Students have to cooperate and complete a project as a member of a group. That process involves many things that are completely the choice of each team, such as the use of weekly progress reports, work statements, written comments on each other's written materials, etc. However, four things are absolutely required of all: participation in a group interim draft project report; submission as a team partner of the complete project report; making two oral presentations to the class furthering the project; and commenting on others' class presentations or completing any other formal measure of class participation.

Due to work schedules and personal issues some individuals persist in viewing a project course as one that has optional class attendance. This has caused me to consider imposing two requirements. The first is that students must attend 60 % of the course meetings to pass. The second involves loss of a full letter grade if more than 20 % of the meetings are missed. On the other hand, lateness, while at least irritating, and certainly harmful, introduces the opportunity to vary the course. Hence until now I've not created a similar penalty system for late or partial attendance. Instead I used interesting throw-away topics. Figure 1 shows some items presented during initial minutes of the Winter 1996 course. Any regular latecomer is doubtless unaware of some, and likely unclear about most, of these items.

Although many of these questions involve mathematics, a few explicitly involve words, and some involve strings of information. All were part of a management strategy that sought to get better exposition. Here better differs from longer. Terse writing, use of outlines, spatial organization, images, and existing mathematical notation, all gain and hold audience attention, an essential in communicating project accomplishment.

There are many topics that were put forward to the class when only a few people were present. Some concerned engineering, architecture, linguistics, communication, computer networks, and coding. I explored students' knowledge and openness to learning the subject since mathematics is a gateway into science, engineering and computing.

Approximating π ... and Creating a Visual

Although the course required nothing on mathematics, I brought up several math topics, whenever a large portion of the enrolled students came late to class. In one such discussion I gave out the four π approximations 3, 22/7, 355/113, and (2143/22)^0.25 and declared those values to be source material for everyone to present percent-error-to-actual- π to the class via a visual. The first visual was an off-hand chalk-talk based on numbers obtained from a Sharp EL-506A Scientific Calculator. Those numbers involved zero deviation to true π for the last two approximations. This was on a calculator with ten-digit display and an added two digits for exponents, allowing very large/small numbers. Since it was clear that greater visual and mathematical sophistication and higher computational accuracy is easily obtained by students in the course, the issue did not stop with that one presentation. Over the remaining weeks at least six other students gave presentations showing something about π such as its approximation or other facts about it. The visuals were often very intersting. They conveyed a large number of facts about π most of us had not known. One example of this was a student presentation that listed the value of π from the Egyptian Ahmes Papyrus, sometimes called by its discover's name, Rhind (or with Ahmes' name indicated by A'h-mose): 4(8/9)2 = 256/81 = 3.16049. (The same item was the corner stone of a subesequent-term course presentation by another student.) Another student presentor stated that the approximation to π we would write as 3 + 177/1250, was known in India about 580 A.D.: the value is correct to 0.002 %

The first successful internet activity was locating world wide web (WWW) material on where birthdates'-number-strings appear in π . There the sense that seeking information could be a venture of interest for itself was the key contribution of a presentation by Ariana Menhenett. Her contribution is listed in Figure 2 below, a tabulation of the WWW universal resource locators (URLs) that came out of the search we began, along with some book references on π . A visual very similar to that figure was given out as a hard copy class handout before any project team had completed an intermediate/interim draft project report, to illustrate the process of titling and organizing information. Traditional resources, i.e., libraries, also proved useful in locating information. Dan Delsol consulted an encyclopedia to obtain thirty digits of π[8].

Table 1 following Figure 2 is adapted from a presentation by Dominic Tham: use of the world wide web to locate the URL http://www.mind.net/xethyr/numbers/approxpi.htm. Tham's presentation compared two numbers he extracted from the computer resource (the URL), the actual number of accurate digits in the approximation, and the number of digits in the ratio that achieved that value. This innovation, asking that we look at a fact that had not previously been considered, enlivened what he'd found on the web. He executed the required task of choosing a topic and composing an illustrative figure. The item presented here as Table 1 is based on his work (this figure has revised titles, key/credit information, and rearranged data.). Table 2, taken from an email message sent by Dan Delsol, takes another view of the issue of approximating π . It illustrates students' willingness to combine course assignments, and make dry exercises relevant. Table 3 relates the use of information in Figure 2 to rapidly-create &pi: -birth-date results: a hard copy visual similar to this table was distributed to the class.

Some students varied the presentation subject from π . Even when they were giving talks nominally comparing the four approximations' error, student presentors discussed a wide range of mathematical and historical facts. While one talk was based on a hard copy encyclopedia, most involved World Wide Web sites found by students (see Figure 2). One visual-creation-focussed presentation concerned the growth of internet usage. Since vary the problem is a common tip, we considered other π approximations based on strings of words: they enabled requiring yet more data entries in a visual constructed to compare approximations' error. Further detail on that appears below in Figure 3. We covered much more about π , the circular and hyperbolic functions (e.g., see [1, pp. 71-79, 83-89]), and many other topics in π and e, but conclude here, in order to turn to the slowly converging infinite product Π .

Computing and Mathematics Applied to Approximating a Slowly-Converging Infinite Product Π

We used a geometric diagram and associated limit from [3] called to my attention by W. Lushbaugh as a tool to portray two things. First we showed how to convey a theme with a visual. This involved use of keys (text and symbol fields within the figure), titles, coordinate-axis-labels, and other aspects of data organization. Second, we investigated a range of computing resources available to most of us, and their limitations. The limitations arose because of the nature of the limit, an extremely-slowly converging infinite product. By doing the naive direct computations (and in a varied set of computing contexts), I used the new information about computing, numerical analysis, and fundamental topics in mathematics that resulted from the in-class dynamic to prepare and present in class a series of summarizing handouts. As in the case of approximating π , students' responses located useful material expanding all of our horizons.

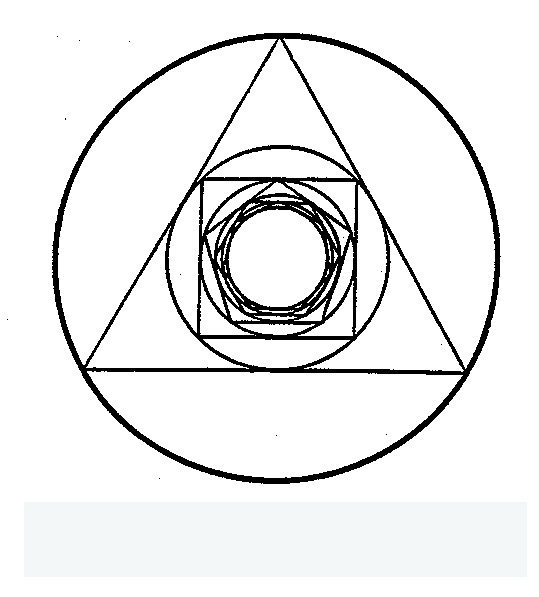
The figure in [3], reproduced here as part of Figure 4, shows successive circles and inscribed polygons in a sequence. The beginning circle has a unit radius and an inscribed equilateral triangle. The next circle is inscribed within the triangle, and there is a square inscribed within it. This proceeds, increasing the number of sides by one at each step (so that the next inscribed item is a pentagon), inscribing another circle within the last polygon, and so forth. The inscribed circles get closer to the polygonal boundaries, so the value of the declining radii of successive circles ultimately approaches a limit. An analytic expression for that limit follows from trigonometry. It is:

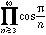
Figure 5 is optimistic in two ways. First, it includes an extremely coarse upper bound to the limit. Second, it uses Mathematica [4] to estimate the infinite product limit, and that proved to be very inefficient in terms of running time, when the direct approach was employed. In that case Mathematica-computed the value of 0.1149704084 by truncating the product at 20,000. While that value is much closer to the actual limit than the calculator upper bound, it took over twenty hours for Mathematica to interpret such a large expression. The calculator estimate seemed large after truncating at 36, so a quick-computation of an upper bound was based on cos(π/100) and other values. That "coarse bound value" was 0.1310485449.

The problem with all these quick estimates lies in the slow rate of convergence of the infinte product. The remedy was conveyed to me by Prof. Elliot Landaw, via computer message: use the rapidly-converging series for log(cos). His result for the limit is 0.1149420448532962. Through C-programming assistance from Michael McNally and Eskandar Ensafi we were able to move beyond Mathematica performance limitations. Their programs made direct computation beyond truncation at 20,000 practical, something that isn't possible in Mathematica. However, experiments showed that no direct evaluation of the infinite product gets a remotely close value to the ultimate limit. The initial question to the class was get close to the infinite product limit as people had done hundreds of years ago by adding successive digits to a p approximation. E.g., the mnemonic devices of Figure 3 give twenty or thirty digits: neither is feasible for the infinite product by direct computation.

Direct evaluation is ineffective because the change in the product is extemely small when adding more cosine factors. McNally's code ran on a Sun SPARCstation 4. It obtained a result for 1,000,000 in seconds. That led to a better infinite product value: for a truncation to 10,000,000 it gave the limit-estimate 0.114942101576559. A revised version of that program by Ensafi with several useful control features, was run out to 1,000,000,000 on a 133 Mhz Pentium. It obtained the direct limit-estimate 0.114942046095759. Landaw's approach avoided the slow-convergence of the cosine product and "required a few seconds on a 386 machine." It was based on "Taylor series expansion ... using log ... ." It yielded a smaller value of 0.1149420448532962 , something previously published by Bouwkamp, who took the same approach.

While Figure 5 and other items reporting the above were distributed to the class in the form of handouts, Mounitra Chatterji worked using a mixture of computer network and UCLA library resources. He located (with a little help from his instructor, and little is a key adjective here) three published papers and a computer-message series explaining how to accurately calculate the infinite product in question. Figure 4 also lists the publications and the email locators for the individuals involved in the message-exchange. The 1965 published items by C. J. Bouwkamp take the same tack as Landaw and result in the identical value. The 1990's publication's author was at that time an undergraduate student; Tamara Curnow explains in detail the series to use, and gives an inferior value of " ...certainly very close to 0.1149420446 ... ". Figure 6 conveys email that led to more being learned about the infinite product, including a much greater number of digits (although verification isn't certain): the individual responsible was Mounitra Chatterji, and the key author was Ron Bruck at USC.

The class response to a question about the Riemann zeta was only recall of the name being associated with integration in calculus. My own knowledge was meager and limited to knowing that I'd seen it once. We all learned a lot more. Though this item came up because Bruck and Landaw both employed the Riemann zeta function, it is typical of the kind of learning that was stimulated by the group experience. Bruck describes the Riemann zeta's role; he also gives ways to use other features of Mathematica to derive his lengthy result. I used Mathematica's help function to define the Riemann zeta, and then plotted the function using Mathematica's graphics capabilities. The result was distributed as part of a class handout: that item is essentially the same as the curve in Figure 7.

Conclusion

This course presented inquiry as a valuable effort for its own sake. Yet it did so in order to illustrate fundamental issues concerning team work, project design, and preparation of a professional report and a convincing talk. The issues that were used include π and a slowly converging infinite product &Pi . Notwithstanding the mathematical character of these two principal issues, the inquiry also ranged over words, history, and many other abstractions.

The course began with a list of twenty possible projects, each presented by a brief title and a few lines of text. One of those involved jitney transportation. When I failed to obtain a definition of jitney in response to a question from a member of a team that chose that project, from my on-line dictionary (Webster.app), I called the library reference desk. The librarian there read the following to me:

Jitney: 1. A five cent coin; nickel. 2. A small bus or car, especially one travelling a regular route that carries passengers for a low fare, originally five cents. [6].

I never would have known the link between a word fixed in my mind as relating to transportation, and a coin, had I not listened to, and sought to answer that question.

One rationale for considering these abstract issues, is that some cases involving puzzling computer algorithms have yielded to further inquiry. E.g., I. Vardi wrote a Mathematica program, and in its comments stated: The Collatz problem, Also Known as The 3x+1 Problem, which terminates ... if an iterate reaches one of ... 4 known cycles. ... program run(s) on positive and negative integers. (My emphasis indicated by underlining.) [The three other cycles are: {-1} ; {-5, -7, -10} ; {-17, -25, -37, -55, -82, -41, -61, -91, -136, -68, -34}.]

Rather than see mathematics as past, since students were finishing their major toward a degree in computer science, I considered it to be a world they could explore ... and possibly create new results. In one case I asked them to consider the largest odd factor in the dates of the class meetings that week, 22696 and 22896. The question was: Are 2837 and 1431 prime? Again Mathematica provided a fast response. Yet the entire issue leads to yet another question for the next offering of the course, possibly the core of an extremely ambitious project. A draft of the statement for presentation to the next Computer Science Design Project course could be:

Tools to Explore Goldbach's Conjecture (Factual statements derived from [7])

In 1742 Goldbach conjectured that every even integer greater than 2 is the sum of two primes. This has been verified for all even numbers less than 100,000 but no one has been able to prove it. Create a computer program to assist in exploring whether the conjecture holds true.

The value of the project is not only in the result. It is also what happens to the people in a project team as they strive toward achievement. This note records some of those strivings.

References

[1] Abramowitz, Milton and Stegun, Irene A., eds., Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, National Bureau of Standards, Applied Mathematics Series 55, June 1964, 10th printing December 1972, Washington, D.C.: U.S. Government Printing Office.

[2] Lagarias, J. C., "The 3x+1 problem and its generalizations," American Math. Monthly No. 92, 1985, pp. 3-23.

[3] Kasner, Edward and Newman, James R., Mathematics and the Imagination, NY: Simon and Schuster, 1940; Redmond: WA, Tempus Books of Microsoft Press, 1989; pp. 310-312;

[4] Wolfram, S., Mathematica, A System for Doing Mathematics by Computer, NY: Addison-Wesley, 1988, 1991.

[5] Pierce, B. O., A Short Table of Integrals, Third Revised Edition, NY: Ginn and Company, 1929.

[6] Webster's New World Dictionary, 2nd Edition, 1984, p. 759.

[7] Stark, Harold, An Introduction to Number Theory, Chicago, Illinois: Markham Publishing Co., 1970, Cambridge, Massachusetts: The MIT Press, 1979, second printing, p. 5.

[8] Larousse Enclopedique en Couleurs, Vol. 17, Paris France: France Loisirs, 1979, p. 7244.

The truth of: Any natural number cubed can be represented as the sum of adjacent odd numbers.

How to write a sum of adjacent odd numbers: totalling 113 .. . 83 ... 173 .

The meaning of serendipity. The historic and geographic origins of that word.

Rapidly evaluating the approximate value of 2⁶⁴ .

How to play the checker game invented by Lasker.

If about twenty identical paper clips are linked and the entity is suspended from its end points, what is the name of the resulting curve?

The approximate value of e²⁵.

The best approximate value of π given as a ratio of numbers of two or fewer digits.

The best approximate value of π as a ratio of three digit numbers.

The best approximate value of π as a ratio of numbers involving a total of six digits, and two square root operations.

An easy way to recall the 17 th digit of π following the decimal point.

Is there a way that an ordinary paper clip attached to a nylon string can balance a two-ounce weight, i.e., keep the latter from falling?

What is the relationship of the hanging chain curve to the exponential?

The relationship of wrapping friction, the use of exponents, and the quantity π.

Relationships involving the circular and hyperbolic functions.

An easy way to recall the tenth digit following the decimal point in e.

Computer Sources

Where is your Birthday in PI? http://www.facade.com/fun/amiinpi/ (1)

Search Pi, a program by Jeremy Gilbert; see: 2_and_a_half_million_digits_of_pi

http://gryphon.ccs.brandeis.edu/~grath/attractions/gpi/index.html (2)

Jeremy Gilbert, <grath@cs.brandeis.edu>, wrote ... scan first 10 million digits of PI ... from ...

http://www.hepl.phys.nagoya-u.ac.jp/~mitsuru/pi-e.html . (3)

Michael McNally recommended Pi_through_the_ages:

http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html (4)

Also see The Pi Page :

http://www.ccsf.caltech.edu/~roy/pi.html (5)

Rational approximations to π found by Dominic Tham are at:

http: //www.mindnet/xethyr/numbers/approxpi.htm (6)

Program at (6) is by Sage Weil<sage@mind.net >; he mentions 1.2 million digits of π at:

ftp://uiarchive.cso.uiuc.edu/pub/etext/gutenberg/etext93/pimil10.txt (7)

Search on pi, math brought up (1), (8), and (9), three items all contributed by Ariana Menhenett.

http://www.MathProPress.com/math/notation/pages (8)

http://id.mind.net/~lutusp/pi.htm (9)

Book Sources

Borwein, Jonathan M. and Borwein, Peter B., Pi and the AGM [BB 87]

Alternating arithmetic and geometric means compute p.

Beckmann, Petr, A History of Pi [Be 71]

Expository review of ideas related to p.

Barrow, John D., Pi in the Sky - Counting, Thinking, and Being [Ba 92]

The place of mathematics as a model of the world.

(R1) was soon bettered by Ariana Menhenett's memory of the sounds of the first thirty digits in π in Chinese [we refer to this as (R2)]. (Since then another student in a subsequent offering of the design project course has told me that he knows thirty-four digits from their sounds as Chinese numbers.)

That was equaled by Dan Delsol who contributed (R3), the following French language (here punctuation does not count as letters/digits) mnemonic device :

The French in (R3) appears in [8] Larousse Enclopedique en Couleurs, Vol. 17, Paris France: France Loisirs, 1979, p. 7244.

My notes indicate that Ariana Menhenett found the expression (R4) for 3.14159265358979323846264:

Nested-Circle-Polygon Diagrams (from Kasner and Newman, op. cit.)

Computer-Based Sources

Ronald Bruck <bruck@pacificnet.net> (1)

Kevin Johnson <ha9705@hocr2n37.london.waii.com> (2)

Xander Kenobi <kingauss@wam.umd.edu> (3)

Eskandar Ensafi <esky@cs.ucla.edu> (4)

Elliot Landaw <elandaw@biomath.medsch.ucla.edu> (5)

Journal and Book Sources

Bouwkamp, C. J., "An Infinite Product," Indagationes Mathematicae, 27, 1965, pp. 40-46; also published in Ned. Akad. Wet. 68. [Bo 65]

Curnow, Tamara, "Falling Down a Polygonal Well," Mathematical Spectrum, 26, 1993/1994,

pp. 110-118. [Cu 93]

Kasner, Edward and Newman, James R., Mathematics and the Imagination [KN 40, 89]

Pierce, B. O., A Short Table of Integrals [Pi 29]

Wolfram, S., Mathematica, A System for Doing Mathematics by Computer [Wo 88, 91]

From: mounitra@seas.ucla.edu

Return-Path: bruck@paci Organization: University of Southern California Date: Thu, 15 Feb 1996

Newsgroups: sci.math References: 1 2 3 Subject: Infinite Product

In article <bruck-1502961848200001@max-27.pacificnet.net>, bruck@pacificnet.net (Ronald Bruck) wrote:

:In article <4g0ko6$r8u@airgun.wg.waii.com>, :ha9705@hocr2n37.london.waii.com (Kevin Johnson) wrote: : ::Xander Kenobi (kingauss@wam.umd.edu) wrote:

...(what's the value of)

: ::> inf. ::> PI cos(pi/n) ::> n=3 :: ::approx 0.114942 ::i let this go a lot farther, but i began to question the cos() function i was ::using. Anyway, I don't see any obvious expression to get this number. Anyone?

:A suggestion for numerical computation: use the series for log cos x, : :

log cos x = -x^2/2 - x^4/12 - x^6/45 - (17*x^8)/2520 - (31*x^10)/14175 - ... : :and sum this for x = pi/n for n = 3 to infinity. You get something :involving the zeta function of even values Then exponentiate at the end. :Hmmm. But the series must diverge when x = pi.

Yes, that's the ticket. In Mathematica:

logcos = Normal[Series[Log[Cos[x]],{x,0,60}]]; from100 = logcos/. x^n_ -> Pi^n(Zeta[n] - Sum[1/k^n,{k,1,100}]); from100dec = N[from20,100]; val = Product[N[Cos[Pi/n],100],{n,3,100}] * Exp[from100dec]

The result is

0.11494204485329620070104015746959874283079533720086351684402339651896601282535305117794

The idea is to compute, say, \prod_{n=101}^\infty cos(\pi/n) by taking the log. The first line of Mathematica gives the series representation, up through degree 60 (the Normal strips off the O() term and converts logcos into a polynomial). We then substitute x = Pi/n from n = 101 to infinity and sum. Mathematica knows the values of Zeta[n] for even n in terms of Pi and the Bernoulli numbers, so from100 is an exact expression, no numerics involved. The next line converts it to 100-place decimal. The final line exponentiates from100dec to get the product from 101 to infinity, and then multiplies by the 3..100 terms.

You can probably do it with a lot smaller numbers than 60 and 100. The answer stays the same if you increase the 60 or the 100. The whole thing took about 49 seconds on a Power Macintosh 9500/132.

I still prefer the interpretation that it's the average value of

cos(Pi * (1 \pm 1/2 \pm 1/3 \pm 1/4 \pm 1/5 ...)), \pm = plus-or-minus.

--Ron Bruck Now 100% ISDN from this address

-------------- hope it helps, mounitra@seas.ucla.edu

s 0.2 + 0.3i 0.0002 + 0.0000003i 0.00000000002 + 0.00000000003i

z (s) -0.579485 - 0.38703 i -0.500184 - 2.75802 10-7i -0.5 - 2.75682 10-11i

| z (s) | 0.696846 0.500184 0.5

s 0.25 0.0002 0.0000002

z (s) -0.813278 -0.500002 -0.5

| z (s) | 0.813278 0.500002 0.5