Visual Material and Applied Science Education

a working draft by Allen Klinger, © and last revised 9/16/2004

http://www.cs.ucla.edu/~klinger/macaroni.gif

Tradition and Creativity

Through life people develop and learn in what is best described as set ways of thinking. In [2] Adams presents the value of visuals in breaking free of modes that prevent problem solution. Teaching mathematics often entails stress on logic and formalism. Reforms there have stressed the role of common sense in problem solving. We agree that many mathematical problems have formula/set-algorithm approaches to finding their solution. However we stand with the diverse cultures described in [1] and their innovations, rather than the transmitters of formal methods. Mathematics education should stress creativity and free thinking. We see visual materials as one way to transmit existing mathematics while stimulating thoughtful and innovative education.

Strong traditions in the mathematics community determine instructional boundaries. A modern view appears as the result of work by the Mathematical Sciences Education Board in [3]. There six major categories are described, Pattern, Dimension, Quantity, Uncertainty, Shape, Change.

Foundations

The wide availability of hand calculators changed the need for knowledge: long division and square root algorithms, logarithms, and the contents of trigonometric tables are easily obtained when needed. Yet thought challenges must remain for students. Here are four questions that lead current pupils to wrestle with issues that are something like the things indicated in [1, 2]:

---

1. What is half of eleven?	Binary Variation
2. What is one-half plus one-third?	Baseball Arithmetic
3. Can one arrange nine apples in four baskets so there are an odd number of apples in each basket?	Distribute Apples
4. Can one divide a circular pizza pie into eight exactly equal slices with just three straight line cuts?	Divide Pizza

Each of the above items in Table 1 leads to a range of possibilities. Innovative solutions in [2] regarding joining nine dots arranged in a square array by a continuous sequence of four straight lines are of the same kind. Thinking outside the box, the terse description of the simplest answer to that problem, opens people to the notion that there are several possible answers. Just how true that is is revealed when one views Figure 2, a class presentation image.

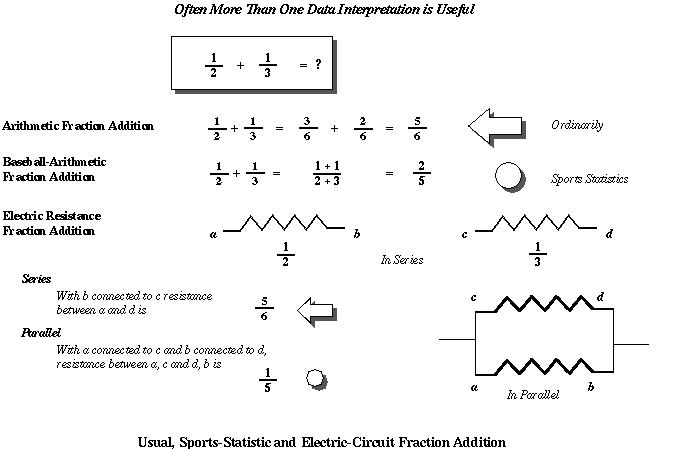
Concepts can be shown. That may be by a single sketch, a series of panels (comic or cartoon style, animated sequence), or a static illustration as in Figure 2. Creativity in mathematical ... or indeed any type of ... problem solving can be supported or inhibited by pictorial means.

Significant differences in reasoning about a teacup and saucer would follow if they were presented via the left part of Figure 3 rather than the two distinct entities in the remainder of that image.

---

Figure 3. Different Concepts of Teacup and Saucer(G. Wu)

Some results from ancient cultures that remain part of our mathematics curriculum can be visually communicated using color animation. For an example we turn to the Pythagorean Theorem. This relationship between the three sides of a right triangle was known in ancient Babylon and Egypt beginning about 1900 B.C., but not widely publicized until Pythagoras. He stated explicitly that for a right angle triangle (i.e., one angle is 90^o), the square of the hypotenuse is equal to the sum of the squares of the other two sides:

---

a2 + b2 = c2

Figure 4. Pictorial and Algebraic Representation (D. Lau)

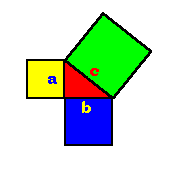
The green square has area c² that equals the sum of two others: exactly the sum of yellow - a² - and blue - b² - measurements.

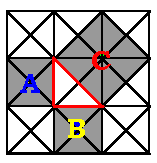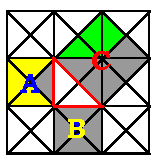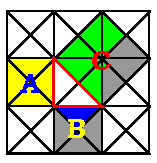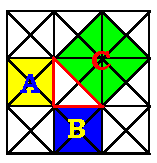
That color animation makes this vividly reasonable for an isoceles triangle special case follows in Figure 5, also by Dorene Lau.. By counting green triangles we quickly see that it is the total of yellow and blue ones.

---

Figure 5. Isoceles Triangles and Pythagoreas' Result (D. Lau)

---

Architecture and Decoration

Images of Maori buildings in [1] show beams that are both integral parts of the structures, and highly decorated in an ordered, mathematical design. Images from other cultures, ibid. present the rich visual heritage of people over the world. The analysis in [1] validates the clear perception those people had of concepts we would associate only with the most esoteric branches of the mathematical knowledge tree.

Practical Calculation in Arts and Commerce

Few today would pursue the even-handed division practiced in ancient Egypt. Nevertheless, their use of integer fractions has an element of fairness not found in contemporary partitioning schemes. The general subject of partitioning and keeping track of decompositions of quantities is covered in [4].

Figure 6. Partitioning a Scarce Resource (See [4])

Dr. Stelling read the above and "wondered about ... solution (to satisfy)

a) all portions are identical (not just in size, but also in makeup;
b) each portion has the minimum number of pieces possible; and
c) subject to a) and b), the size of the smallest piece is maximized.
d) [alternative to c)] subject to a) and b), the number of cuts is minimized.

(He suggested) ... divide 5 loaves into halves, and the remainder into fifths, so that each portion consists of
1/2 + 1/5 + 1/5.
... by examining alternatives ... this solution satisfies all the conditions."

Early Efforts

Computing the area of the lune, an illuminated region of the moon seen from earth when much of that body is in the shadow of our planet, is described in [6]. The image of Figure 7 is an early understanding of the concept of limit.

Figure 7. Visual Representation of Limiting Process (See [7])

Space division is present in Figure 7 and the fourth question about dividing a pizza. Number division was the subject involved in both Figure 6 and the way that written Egyptian material dealt with fractions [4]. There are many number division facts. Some are known but not proven. Others were proven only after failed attempts by a mathematician of such outstanding ability that his genius stands comparison to that in music of both Beethoven and Mozart.

Key Name	Status	Concerns	Property (Pattern)
Goldbach	Conjecture	Even Numbers	Always A Sum of Two Primes
Lagrange (Euler)	Proven	Every Number	Sum of At Most Four Square Numbers
Nicomachus	Proven	Every Cube	Sum of Adjacent Odd Numbers

Table 2. Numeric Partitions - Questions and Knowledge

The cover page of [9] states "In 1770, Waring made the statement that every number is expressible as the sum of 4 squares, or 9 cubes, or 19 biquadrates, and so on. ..." The omitted statements there impinge on the above item listed in Table 2 under Lagrange. Although [9] is so popular as to be reprinted five times over a span of two generations, much about them cannot be found in its 190 pages. Yet the issue interests more recent authors. Knuth concluded that a pattern exists in the number of partitions of n, part(n), i.e., "the number of different ways to write n as a sum of positive integers, disregarding order," [9], and, from [9]:

5 = 1 + 1 + 1 + 1 + 1 = 2 + 1 + 1 + 1 = 3 + 1 + 1 = 2 + 2 + 1 = 3 + 2 = 4 + 1

part(1) = 1, part(2) = 2, part(3) = 3, part(4) = 5, part(5) = 7 (see [9])

Conclusions

The ordinary person in diverse societies has a good grasp of some mathematical concepts. People in large U.S. cities follow baseball in the summer months and gain knowledge about statistics. In Polynesia, visual patterns of great complexity show understanding of symmetry.

Yet the subject of mathematics is vast and changing. The issue of "fundamentals" and which of them should be taught and how, is expressed by an eminent mathematical educator who proposes teaching mathematical subjects by "encouraging students to explore patterns" ([3, p. 8]).

There is a method for validating accomplishment in absorbing fundamental knowledge and stimulating searching inquiry to grow. It is based on allowing thirteen answers to simple statements with three alternative conclusions. One answer indicates no knowledge. Three others say only that one of the alternatives is clearly wrong. The remaining choices (all thirteen appear as the letters a through m in the following figure) enable introducing one's partial knowledge.

Educational material can be formulated for test and evaluation using multiple-choice answers indicated in Figure 8. Test results to distinguish those learning and progressing within the organized material and others who remain unsure (or, worse, convinced of mistruths) [8].

Figure 8. Three Completions With Thirteen Responses (E. Ensafi)

Appendix

Some subjects can be used for either of two purposes: encouraging interest in mathematics; or moving toward acquiring some quantitative knowledge needed for success in a practical field. Bases for Counting, below, opens paths to electrical engineering and computer science. Simple statements with three alternative conclusions can be constructed for monitoring progress in subject knowledge acquisition using quizzes based on Figure 8 answers [A.1].

Bases for Counting

Generally we use counting by tens, and that many symbols in a single place. Specifically 0, 1, 2, 3, 4, 5, 6, 7, 8 or 9. Computers count with zeroes and ones, only two symbols. The word binary describes that unfamiliar way of counting. It seems odd to begin again after one. But dozens (eggs), sixties (minutes/seconds), and sevens (days), all involve restart based on something other than ten. The word base calls out exactly how many different values appear until one needs a second symbol (in a place notation number representation system).

Since binary facilitates working with digital computers, two, eight and sixteen, even numbers found from repeated multiplying of two, are important in modern technology. They are used for counting and for writing numbers via symbols. The same things done when the base is ten and hundred, thousand, million become easy to recognize happen in systems with two, eight or sixteen for the base. The names for those systems and a number example follows.

Binary three, 11. That symbol is nine in octal. In hexadecimal it stands for seventeen. The following figure expands several representations of the quantity sixteen:

Symbols for	Number Base	Usable Elements	Each Place's	Sixteenbase
Sixteen	Radix System Name	Single Place	Values Powers of Radix	Written
||||| ||||| ||||| |	Sixteen Hexadecimal	0 1 2 3 4 5 6 7 8 9 A B C D E F	[256,257, ...,4095 = 163-1= 212-1], [16, 17,...,255 = 162-1], [0,1,..., 15 = 161-1] 4096, 256, 16, 1	10
V ||||| ||||| |	Fifteen	0 1 2 3 4 5 6 7 8 9 A B C D E	[225,226,...,3374 = 153-1], [15,16,...,224 = 152-1], [0,1,...,14 = 151-1] 3375, 225, 15, 1	11
X ||||| |	Fourteen	0 1 2 3 4 5 6 7 8 9 A B C D	[196,197,...,2743 = 143-1], [14,15,...,195 = 142-1], [0,1,...,13 = 141-1] 2744, 196, 14, 1	12
X V I	Thirteen	0 1 2 3 4 5 6 7 8 9 A B C	[169,170,...,2196 = 133-1], [13,14,...,168 = 132-1], [0,1,...,12 = 131-1] 2197, 169, 13, 1	13
XVI £	Twelve Duodecimal	0 1 2 3 4 5 6 7 8 9 X L	[144,145,...,1727 = 123-1], [12,13,...,143 = 122-1], [0,1,...,11 = 121-1] 1728, 144, 12, 1	14
XVI ¢	Eleven	0 1 2 3 4 5 6 7 8 9 X	[121,122,...,1330 = 113-1], [11,12,...,120 = 112-1], [0,1,...,10 = 111-1] 1331, 121, 11, 1	15
XVI ¥	Ten Decimal	0 1 2 3 4 5 6 7 8 9	[100,101,...,999 = 103-1], [10,11,...,99 = 102-1], [0,1,...,9 = 101-1] 1000, 100, 10, 1	16
||||| ||||| ||||| |	Nine	0 1 2 3 4 5 6 7 8	[81,82,...,728 = 93-1], [9,10,...,80 = 92-1], [0,1,...,8 = 91-1] 729, 81, 9, 1	17
16 dollars	Eight Octal	0 1 2 3 4 5 6 7	[64,65,...,511 = 83-1], [8,9,...,63 = 82-1], [0,1,...,7 = 81-1] 512, 64, 8, 1	20
$ 16	Seven	0 1 2 3 4 5 6	[49,50,...,342 = 73-1], [7,8,...,48 = 72-1], [0,1,...,6 = 71-1] 343, 49, 7, 1	22
16 pounds	Six	0 1 2 3 4 5	[36,37,...,215 = 63-1], [6,7,...,35 = 62-1], [0,1,...,5 = 61-1] 216, 36, 6, 1	24
£ 16	Five	0 1 2 3 4	[25,26,...,124 = 53-1], [5,6,...,24 = 52-1], [0,1,...,4 = 51-1] 125, 25, 5, 1	31
¥ 16	Four Quaternary	0 1 2 3	[16,17,...,63 = 43-1], [4,5,...,15 = 42-1], [0,1,...,3 = 41-1] 64, 16, 4, 1	100
16 yen	Three Ternary	0 1 2	[9,10,...,26 = 33-1], [3,4,...,8 = 32-1], [0,1,2 = 31-1] 27, 9, 3, 1	121
||||| ||||| ||||| |	Two Binary	0 1	[8,9,..., 15 = 24-1], [4,5,6,7 = 23-1], [2,3 = 22-1], [0,1 = 21-1] 8, 4, 2, 1	10000

Figure 9. Representing Number - Sixteen

Computers' make central use of binary, octal and hexadecimal (base sixteen) number systems. Comparisons follow below two ways. A Mickey Mouse hand has only four fingers. It represents the indigenous Brazilian people who counted on the spaces between fingers. The table shows correspondences as the commonly understood decimal value varies.

Figure 10. Decimal, Binary, Octal, Hexadecimal

The above could be viewed as only the latest version since historically human cultures have tried varied number systems for tracking quantity. The first recorded use of numbers to represent quantity is from the Sumerian civilization of Mesopotamia where baked clay tablets listed commercial transactions (4000 to 1200 BC). The Sumerians had a positional number system with base 60 - it survives in the way we measure time and angle. [A.2]

Six hexadecimal numbers represent computer-screen colors. We see mixtures of three primary colors, red, green, and blue. Each one is shown on a computer screen at levels that range from zero intensity to a maximum of two-hundred fifty-five. But 256 is sixteen squared. So the three primary colors can be shown by placing the biggest possible hexadecimal two-values, namely FF, in the appropriate place in the six element code, a number that stands for a color. Thus, Red, Green, and Blue, appear in color here, and also in the initial letters that describe the basic or primary RGB color set.


The convention has the first two digits for red; middle two, green; and last two, blue. Here each primary color can have any value between 0 and FF, where a setting of zero indicates absence of that primary color. Setting a color value to FF indicates that the primary color should be used at its maximum value.

---

---

References

[1] Ascher, Marcia, Ethnomathematics, A Multicultural View of Mathematical Ideas, Pacific Grove CA: Wadsworth, Brooks/Cole Publ. Co., 1991.

[2] Adams, James L., Conceptual Blockbusting, San Francisco: W. H. Freeman, 1974.

[3] Steen, Lynn A., On the Shoulders of Giants, New Approaches to Numeracy,, Washington, D.C.: National Academy Press, 1990.

[4] Gillings, Richard J., Mathematics in the Time of the Pharaohs, Cambridge, MA: The MIT Press, 1972; NY: Dover Publications, Inc., 1982.

[5] Kline, Morris, Mathematics for the Nonmathematician, New York: Dover, 1985.

[6] Dunham, William, Journey Through Genius: The Great Theorems of Mathematics, NY: John Wiley & Sons, Inc., 1990.

[7] Kasner, Edward, and James R. Newman, Mathematics and the Imagination, NY: Simon and Schuster, 1940; ISBN 1-55615-104-7 Redmond: WA, Tempus Books of Microsoft Press, 1989.

[8] Klinger, Allen, Experimental Validation of Learning Accomplishment, Proceedings of the Conference on Frontiers in Education, 1997; see CSD Tech. Report 970019, http://www.cs.ucla.edu/~klinger/csd_report.html.

[9] Davenport, H., The Higher Arithmetic, Fifth Edition, Cambridge University Press, 1952, 1984.

[10] Knuth, D.E., Fundamental Algorithms, The Art of Computer Programming, Vol. 1, Addison-Wesley Publishing Company, 1978.

[A.1] Klinger, Allen, Experimental Validation of Learning Accomplishment, CSD Tech. Report 970019, http://www.cs.ucla.edu/~klinger/csd_report.html.

[A.2] http://www.hebb.cis.uoguelph.ca/~deb/27190/