

 Complex Terms
Complex Terms


|


|
%A DB of flat parts described by their geometric shape and weight.
%Different geometric shapes require a different number of
%parameters. Also actualkg is the actual weight of the
%part, but unitkg is the specific weight where the actual
%weight can be easily derived from the area of the part
query: part-weight(No, Kilos)
part-weight(No, Kilos ) <- part(No, _ , actualkg(Kilos)).
part-weight(No, Kilos ) <- part(No, Shape, unitkg(K)),
area(Shape, A), Kilos= K * A.
area(circle(Dmtr), A1) <- A= Dmtr * Dmtr * 3.14/4.
area(rectangle(Base, Height), A1) <- A1= Base*Height.
% part# shape , weight
part(322, circle(11), actualkg(34)).
part(121, rectangle(10, 20), unitkg(2.1)).
In computing this query on the first part we find that
the goal in the first rule yields No=322 and
Kilos=34 (the operation by which this goal and fact
are made equal is called unification).
The goal of the first rule fails to unify with the first fact,
and instead unifies with the second one, yielding
No=121, Shape=rectangle(10, 20), and K=2.1.
Unsing these values, the area rules compute A
and then then Kilos.
part(socks, [red, black, blue]).From these facts we might want to list all the items, colors pairs (i.e., deriving a flat relation from a nested one) as follows:
query: part-color(Item, Color) part-color(I, C) <- allcolors(I, [C|_]). subL(I, Rest) <- subL(I, [C|Rest]). subL(I, CL) <- part(I, CL).
|


|
father(joe, {peter, mary}).
father(james, {lucy, arnold, jim}).
father(joe, {ann}).
father(jack, {}).
mother(magret, {peter, mary}).
mother(linda, {john, junior}).
query father(X, S) returns all father facts.
query father(joe, S) returns
{father(joe, {peter, mary}), father(joe, {ann})}
query mother(X, {mary, peter})
returns mother(magret, {peter, mary}),
since {mary, peter}={peter, mary} because the ordering is not
important. In general set equality and unification of set terms
accounts for the commutativity and idempotence properties:
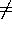 [b, a].
[b, a].
 [a]
[a]
Predicates can be joined on set arguments.
Example: ``create all pairs of parents having the same children''
same_children(X, Y, S) <- father(X, S), mother(Y, S).This rule is equivalent to
same_children(X, Y, S) <- father(X, S),
mother(Y, S1), S = S1.
The equality predicate can thus be applied to sets.
The system supports various
builtin functions on sets, including set union, difference, intersection,
membership, membership, subset_of and the predicate aggregate that
computes
set aggregates.
|


|
father(joe, {peter, mary}).
father(jim, {lucy, arnold, jim}).
Then to list the number of children for each father we can
use a LDL++ builtin called aggr as follows:
query: no_of_children(X, No)
no_of_children(X, No) <- father(X, C_Set),
aggr(count, C_Set, No).
This will return:
no_of_children(joe, 2) no_of_children(jim, 3)Thus, an aggr goal applies the aggregate in of first argument (count in the example) to the set shown in the second argument (C_Set in the example), yielding the value of the aggregate as its thirds argument (No in the example).
LDL++ supports SQL's five basic aggregates:
When applied to an empty set { }, sum and count, return 0, while the other aggregates fail.
As discuss later, LDL++ supports user-defined aggregates.
sup_parts(Sup, <Part>) <-
suppp(Sup, Part, Price), Price >5.
Thus, the pointed brakets denote set of values being grouped by
the remaining arguments in the head.
The sets so constructed can then be used to compute
aggregates. Thus, to count the parts costing more than
$5 sold by each supplier has, we can write:
count_parts(Sup, Cp) <- sup_parts(Sup, Part_set),
aggr(count, Part_set, Cp).
LDL++, however support the computation of aggregates while the
head sets are being computed. Thus, the number of
parts costing more than $5 supplied by each supplied, can be
expressed as follows:
sup_setof_parts(Sup, count<Part> ) <-
suppp(Sup, Part, Price), Price >5.
Therefore, set aggregates can be used directly in the head
of the rules or applied to a set using the
aggr predicate.

|
For a head aggregate such as p(X, count<Y>) <- ... the first argument X is a unique key for the values produced by this rule. Similar rules apply to all other builtins.
q(X, count_dist<Y>) <- p(X, Y, Z). e(X, count_all<Y>) <- p(X, Y, Z). p(a,b,1). p(a,b,2). p(b,c,1).Then query: q(X,C) returns q(a, 1), q(b, 1).
But query: e(X,C) returns e(a, 2), e(b, 1).
Moreover,
g(X,Y,seq<>)<-p(X,Y). f(X,Y,seq_dist<>)<-p(X,Y). p(a, b). p(a, c). p(a, b).Here query: g(X,C,S) returns:
g(a,b, 1) g(a,c, 2) g(a,b, 3).But query: f(X,C,S) returns:
f(a, b, 1) f(a, c, 2).Observe that:
The following table summarizes the built aggregates:
|
Built-in Aggregates in LDL++ |
||
|---|---|---|
| Name | Semantics | SQL Equivalent |
| sum (sum_all) | Compute the sum of items in column including duplicates | SUM |
sum_dist |
Compute the sum of items in column
excluding duplicates |
SUM DISTINCT |
|
avg |
Compute the average of items in column including duplicates | AVG |
| avg_dist | Compute the average of items in column excluding duplicates | AVG DISTINCT |
| count (count_all) |
Count the items in column including duplicates | COUNT |
| count_dist | Count the items in column excluding duplicates | COUNT DISTINCT |
| max | Find the maximum value in column | MAX |
| min | Find the minimum value in column | MIN |
| seq | Compute the sum of items in column including duplicates | Not Applicable |
| seq_dist | Compute the sum of items in column excluding duplicates | Not Applicable |
 Carlo Zaniolo, 1997
Carlo Zaniolo, 1997