

 Database Updates
Database Updates


|


|
Example:
Delete from the city relation all of the cities whose population is below some given threshold Size.
delete_small_cities(Size) <-
city(Name, State, Population),
Population < Size,
-city(Name, State, Population).
export delete_small_cities($Size)
query delete_small_cities(100000)
When applied to the cities database, the remaining facts are:
city(Houston, Texas, 3000000). city(Dallas , Texas, 2000000). city(Huntsville, Texas, 150000). city(Austin, Texas, 750000). city(San Antonio, Texas, 1500000).
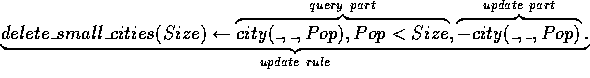
the order of update specification may affect the result. The query part of the program is still declarative as before.
Suppose that the employee relation contains two tuples with the same name but different salaries.
employee(pat, 'CHPC', 1000).
employee(pat, 'MCC', 1100).
We define an update rule to give all employees some specified raise.
raise(P) <- employee(Name, D, Sal), NewSal = Sal * P, -employee(Name, D, Sal), +employee(Name, D, NewSal). export: raise($P)
The goals following an update goal see the results of the update.
Thus, even if Name is a key, no key constraint violation
will follow from this rule.
Updates are not permitted in a recursive rule. The following is incorrect:
where q(Y) itself is recursively defined is ok.
Limitations: no union rules
No union of update rules. Suppose that we want to give somebody a raise
of 10% if his/her salary is below 1000 and otherwise we want to give him/her
a 5% raise.
Using Conditionals instead of union rules
The correct version of the previous program uses the if-then-else predicate.
In
Example: If w(X, Y) can fail in the rule,
The normal solution consists in moving the potentially failing predicate
before the update:
Updates and Assignment as Infallible Predicates
Updates and assignment statements are unfailing (see Infallible Predicates)
and can be used after updates. Thus, the following is acceptable.
IF (Condition ELse True) is Infallible
The result of the execution of the if predicate can succeed even
though the condition within the predicate fails.
Example: This will work only for export:p($X).
Here the ``if'' succeeds even if w(X, Y) fails. The rule can be
modified to work also for export:p(X).
h
Is interpreted as:
h
where pk, k = 1, ..., n-1
are successive versions of the goal p all of which
succeed and with pn the last succeeding goal.
Note that each
Observet that the
forever-goals are also infallible.
Forever: Example
Continue giving 10% salary raises to employees of
the toy department until John's salary exceeds some number N.'
![]()
![]()
![]() Updates: Limitations
Updates: Limitations
Limitations: recursion
p(X) <- p(Y), +b(Y).
This update is incorrect because all of the tuples must be marked
in the query part prior to the updating; this is, as in negation, a
requirement for a stratified program. On the other hand,
p(X) <- q(Y), +b(Y).
raise(Name, Sal, NewSal) <-
employee(Name, Sal),
Sal <= 1000,
NewSal = Sal * 1.1,
+employee(Name, NewSal).
raise(Name, Sal, NewSal) <-
employee(Name, Sal),
Sal > 1000,
NewSal = Sal * 1.05,
+employee(Name, NewSal).
export:raise(Name, Sal, NewSal)
This construct is illegal since we do not know the order of execution of these
rules. We can use the if-then-else construct to overcome
this problem.
raise(Name, Sal, NewSal) <-
employee(Name, Sal),
if(Sal <= 1000 then NewSal = Sal * 1.1
else NewSal = Sal * 1.05),
-employee(Name, Sal),
+employee(Name, NewSal).
![]()
![]()
![]() Failing Goals after Updates
Failing Goals after Updates
No Failures After Updates
![]() failures cannot be tolerated after the update part of a rule for
two reasons: 1) A failure entails the ``undoing'' of the updates to
the base relations---an operation that should be avoided; 2) For compatibility
with relational databases, e.g., violations of integrity contraints, can be
detected immediately.
failures cannot be tolerated after the update part of a rule for
two reasons: 1) A failure entails the ``undoing'' of the updates to
the base relations---an operation that should be avoided; 2) For compatibility
with relational databases, e.g., violations of integrity contraints, can be
detected immediately.
p(X) <- q(Y), -b(Y), w(X, Y).
then the rule might not have a clear meaning. The compiler will
issue a warning.
p(X) <- q(Y), w(X, Y), -b(Y).
In some cases this solution is impractical, because, e.g., we want to
see the result of the update. In such a case we must ensure
that the goal after the update is infallible.
raise1(Name, Sal, NewSal) <-
employee(Name, Sal), Sal <= 1000,
-employee(Name, Sal),
NewSal = Sal * 1.1,
+employee(Name, NewSal).
The derived raise1 predicate is itself labelled as an update
predicate, so it cannot be followed by a failing goal when used
in rules. The compiler checks the condition that no goal is unfailing
after updates and complains otherwise.
p(X) <- q(Y), -b(Y), if(w(X,Y) then true).
p(X) <- q(Y), -b(Y), if(w(X,Y) then true else X="empty W").
![]()
![]()
![]() The Forever Construct
The Forever Construct
The forever predicate in a rule:
 g, forever(p), q.
g, forever(p), q.
 g, p1, p2, ... , pn, q.
g, p1, p2, ... , pn, q.
 operates on the state left by the execution of the previous goal
operates on the state left by the execution of the previous goal
 .
If for some
.
If for some  causes no updates, then there are no
further state changes,
causes no updates, then there are no
further state changes, 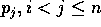 are ignored and we resume with
q.
are ignored and we resume with
q.
iterRaise(N) <- forever(eds(john,D,S), S<=N, raise(toy)).
raise(D) <-
eds(E,D,Sal), Sal1= 1.1*Sal,
-eds(E,D,Sal), +eds(E,D,Sal1).
Note than N is imported into the forever predicate. We
cannot however export values as a result of its execution; therefore,
its effects are manifested throught the update(s) of base relations.
|


|
Using the Parts database, Find the cost of each part P. Then find all the subparts of P, each with their quantity and cost, and compute the total cost. We will augment the Parts database by an additional table cost(Part:string, Cost:integer) which will be updated to contain the cost for each part, basic or assembly.
% Update cost with all basic parts and their costs.
basic_costs <- part_cost(Basic_part, -, Cost, _), +cost(Basic_part, Cost).
% Update cost with all assembled (non-basic) parts and their costs.
assembly_costs <- forever( assembly(Part, _, _), ~unresolved_part(Part),
tally_costs(Part, Total), +cost(Part, Total) ).
% unresolved_part contains those parts for which we do not have as yet a cost
% in the cost relation.
unresolved_part(P) <- assembly(P, Sub, _), ~cost(Sub, _).
% tally_costs sums up the costs of all sub parts making up a part.
tally_costs(P, Total) <- get_all(P, Set_of_subs), aggregate(sum, Set_of_subs, Total).
% get_all computes the sub cost of a sub part by multiplying its quantity times
% the unit sub part cost.
get_all(P, <Prod>) <- assembly(P, Sp, Qty), cost(Sp, SpCost), Prod = SpCost * Qty.
 Carlo Zaniolo, 1997
Carlo Zaniolo, 1997