More on Rules

---

Rules: Definitions
• A rule is an expression of the form:

        A B₁, B₂, ... , B_n.

  where A and B₁ through B_n are predicates. A is called the head of the rule and the expression to the right of the '''' is called the body.

  part_cost1(X, Y) <- part_cost(top_tube, X, Y, Z).
  

• A rule that contains no variables is a ground rule or an instantiated rule.

  run_for_your_life <- physician(`Dr. Frankenstein`).
  

• A rule with no body is a unit clause.

  distance(City, City, 0).
  

• A ground unit clause is fact.

  distance(`Austin`, `Waco`, 110).
  

  Facts are normally stored in the database (but facts occasionally occur in the program.)

Head and Body:

   Semantics of Rules

---

Rules: Union The two rules,

 
      A <- B.

      A <- C.

are logically equivalent to

(B A) & (C A)

which is

(B C) A.

We will refer to a predicate such as A, which is the result of the union of two (or more) rules, as a union predicate.


Rules: Interpretation

A rule,

      A B₁, B₂, ... , B_n.

is logically equivalent to: the conjunction of B₁, B₂, ... , B_n implies A.

When the truth value of each predicate in the body is TRUE, the head predicate is also TRUE.

   Rules: Bottom-up Evaluation

---

(a) h1(X,Y) <- p(X,Y).
(b) h2(X) <- h1(X,Y).
(c) p(X,Y) <- b(X,Y).


    b(1,2).
    b(2,4).

1. Rule (c) is the only one whose body contains only a base predicate. Matching the body with the data produces {p(1,2),p(2,4)} as new facts.
   The partial result is the set {b(1,2),b(2,4),p(1,2),p(2,4)}

2. Now rule (a) can be evaluated using the results of step (1).
   The result is {b(1,2),b(2,4),p(1,2),p(2,4),h1(1,2),h1(2,4)}.

3. Rule (b) is evaluated using the result of step (2).
   The result is {b(1,2),b(2,4),p(1,2),p(2,4),h1(1,2),h1(2,4),h2(1),h2(2)}.

4. No more results are produced.

Equality Predicate

Say that t(X, Y, Z) is a base predicate; X,Y,Z are integers. Then,

sums(X) <- t(X,Y,Z), X = Y + Z.

returns all a,b,c such that the tuple t(a,b,c) appears in t
and a = b + c. The equality serves as a test.

t(3,2,1).
t(5,2,3).
t(8,4,3).
t(7,4,3).
t(7,3,4).

export sums(X); query sums(X) returns {sums(3), sums(5), sums(7)}
export sums($X); query sums(5) returns TRUE, query sums(8) returns FALSE.


Equation Solving

t1(X, Z) is a base predicate; X, Z are integers.

sums1(Y) <- t1(X, Z), X = Y*Y + Z.

Fails at compile time! Although X, Z are known, the system cannot solve the equation for Y.

(The current will however solve simple linear equations.)


Equality Predicate Operating as single Assignment

t1(X, Z) is a base predicate, X, Z are integers.

sums2(Y) <- t1(X, Z), Y = X + Z.

export sums2(X)

compiles correctly! In this form the equality is used as a single assignment.

t1(1,2).
t1(3,5).

query sums2(X) returns {sums2(3), sums2(8)}.
export sums2($X); query sums2(3) returns TRUE, query sums2(4) returns FALSE.

   Safety

---

Safety is a program property that ensures that the values of program variables can be effectively computed.

Safety thus depend on the exectution used (e.g., bottom-up, top-down, or a combination of the two).

1. For the bottom-up execution, the safe predicates are those that are derivable from from database relations (possibly using arithmetic and equality assignements).

2. For top-down exectution, safety also depends from the binding pattern of the export.

3. Assume that goals in the rules are evaluated from left to right. Then the re-ordering of the goals could make a safe rule unsafe or vice-versa

4. The safe binding patterns for equality and disequality predicatess are summarized in the following table.

Safety: Example

good_salary(X) <- X > 80000.

export good_salary(X) does not compile!

• Query form is unsafe.

export good_salary($X) is safe.

• query good_salary(100,000) is TRUE.
• query good_salary(50,000) is FALSE.

In the bound values in the exports are always propagated down to the defining predicates---if these are not recursive. For recursive predicates the situation is more complex and will be discussed later.

Safety: Modified Example

well_paid_employee(Name,Salary) <- 
                employee(Name,Salary), Salary > 80000.

Now

export well_paid_employee(Name,Salary)

is safe.

Arithmetic

Examples of Arithmetic Terms:


Y + Z
X * ( Y / Z)

• All participating variables must be bound to numeric values.
• The result of the evaluated term replaces the expression.
• External functions in C can be incoroporated in the term.

Arithmetic: Precedence



Example: The term A / B * C + D will be evaluated in the following order:

1. .
2. 
3. 

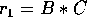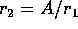
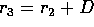
Arithmetic: Result Types

• Integer arithmetic returns integers.
• Mixed (real and integer) arithmetic returns real numbers.

Example:

result(X) <- b(A, B), X = A / B.

b(1, 2).

query result(X) returns result(0) when A,B are declared as integers in the schema, it returns result(0.500) when A,B are declared real numbers.

Arithmetic: Example

Express the distance from Austin to Bastrop in feet

Two equivalent formulations:

distance_feet1(X, Z, W) <- distance(X, Z, Y), W = 5280 * Y.

or,

distance_feet(X, Z, 5280 * Y) <- distance(X, Z, Y).

export distance_feet($X, $Z,  Y).

When the user types:

query distance_feet('Austin', 'Bastrop', Z)

the system returns:

distance_feet( 'Austin', 'Bastrop', 158400 ).
-- 1 solution

``List all cities which are within 100 miles of Austin''.

close(X, Y, Z) <- distance(X, Y, W), W < Z.

export close($X, Y, $Z).

query close( 'Austin', City, 100)

    close( 'Austin', 'San_antonio', 100 ).
    close( 'Austin', 'Bastrop', 100 ).
    -- 2 solutions

The query form: export close($X, Y, Z) will not compile. Why?

Arithmetic: Safety

Also, the program

close1(X, Y, Z) <- W < Z, distance(X, Y, W).

export close1($X, Y, $Z)

will not compile, since W is unbound when used in the comparison. Predicates must be permuted in the body to render it safe.

---