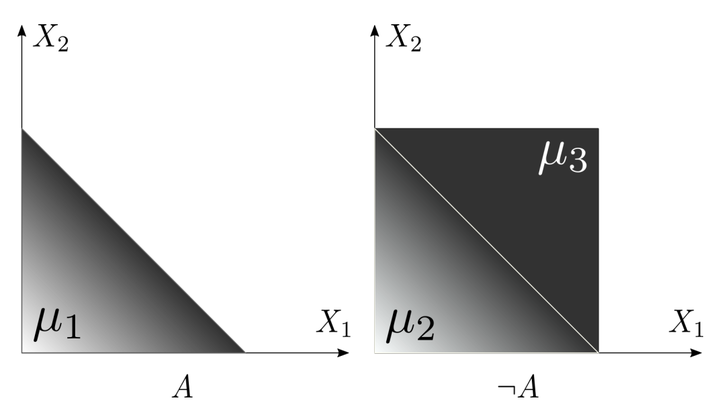
Example WMI Problem
Abstract
Weighted Model Integration (WMI) is a recent and general formalism for reasoning over hybrid continuous/discrete probabilistic models with logical and algebraic constraints. While many works have focused on inference in WMI models, the challenges of learning them from data have received much less attention. Our contribution is twofold. First, we provide novel theoretical insights on the problem of estimating the parameters of these models from data in a tractable way, generalizing previous results on maximum-likelihood estimation (MLE) to the broader family of log-linear WMI models. Second, we show how our results on WMI can characterize the tractability of inference and MLE for another widely used class of probabilistic models, Hinge Loss Markov Random Fields (HLMRFs). Specifically, we bridge these two areas of research by reducing marginal inference in HLMRFs to WMI inference, and thus we open up new interesting applications for both model classes.
Zhe Zeng
Ph.D. student in AI
My research interests lie in the intersection of machine learning (probabilistic modeling, statistical relational learning, neuro-symbolic AI) and formal methods. My research goal is to enable machine learning models to incorporate diverse forms of constraints into probabilistic inference and learning in a principled way.