For this project, your goal is to build a game called Connect N. Connect N is a two-player game, similar to the popular game known by many as Connect 4. In this game, two players take turns dropping checkers (round discs) into a scaffold that is C units wide by L units high. The first player uses red checkers, and the second player uses black checkers. When a player drops a checker into a given column of the scaffold, the checker drops until it reaches the bottom of the column or until it lands on top of another checker in the column. The play alternates until one of the players gets N checkers in a row, either horizontally, vertically, or diagonally.

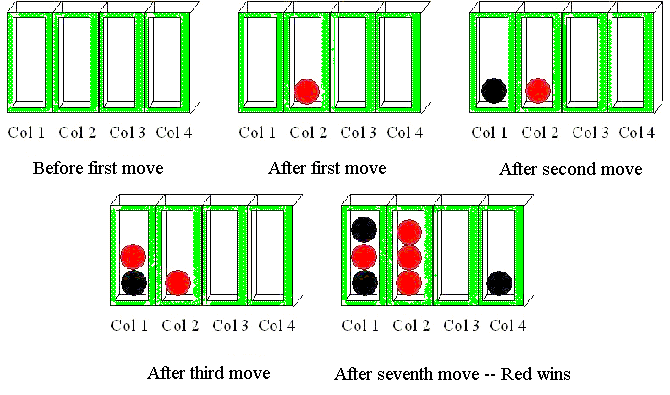
The diagram below shows part of the progress of a game where the scaffold is 4 units wide by 3 units high, and the goal is to get 3 in a row. We start with an empty scaffold, followed by the first player (Red) making a move in column two, followed by the second player (Black) making a move in column 1, followed by the first player making a move in column 1. In the last image, you'll see a completed game where the first player has won.

Your Connect N game must be designed to allow two players to play against each other. Each player will be either a human or a computer player. The computer player's behavior will be embodied in a C++ class described later. You will write different classes for different kinds of computer players. For example, one kind of computer player may be really dumb and just pick an arbitrary one of the columns for its turns. Another may play by considering moves and countermoves, selecting the move it determines is best. Let's see how it might do that.

How to play intelligently

Until you are ready to implement the SmartPlayer::chooseMove function described later, you can get by with just skimming this section and continue reading at the Your assignment section.

Game playing is one area in the field of computer science called artificial intelligence (making computers do tasks which appear to require human reasoning ability). What you want your program to do is somehow model what a human does when playing: Consider the possible moves (and the opponent's countermoves, and the replies to those countermoves, etc.) and select one that is in some way best.

One algorithm for doing this is the minimax algorithm, a recursive algorithm that has been used to implement virtually every two-player game you can think of, including chess, checkers, Othello, etc. Let's first go over some background that will help us to understand the minimax algorithm.

First, some background. A game tree is a technique for showing the game positions for many two player games. Basic game characteristics are:

• There are two players.
• The game is sequential: Players take turns moving.
• The game state can be represented by a board containing all the pertinent information.
• Both players always know the entire state of the game. This is called a perfect knowledge game. This excludes card games with hidden hands, for example, since we would not know all of our opponent's play choices.
• Game moves are not random. (This usually excludes games involving dice or spinning dials.)
• The games are finite: They all reach some terminal configuration representing a win, loss, or draw result.

The initial game board is the shown as the root node of the tree (see below). The children of any node are the board positions that can be reached in a single move. Each branch of the tree terminates in a leaf node that has no further moves and represents a win for one of the players or a draw.

Tic-Tac-Toe, Checkers, Chess, and Connect N are games suitable for game tree representation. Here's a portion of the game tree for Tic-Tac-Toe (also known as Noughts and Crosses, Xs and Os, Tres en Raya, 井字棋, 삼목게임):

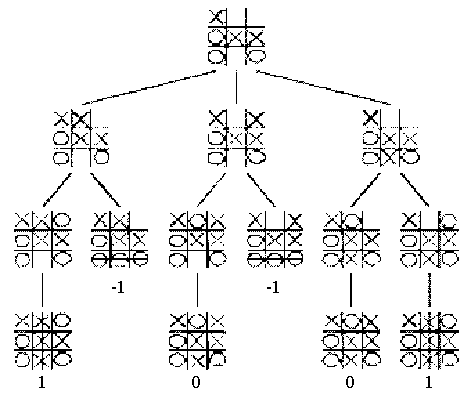
In this diagram "X" winning positions have a value of 1, "O" winning positions have value −1 and ties have value 0. We'll see why in a few minutes.

We call the player who moves first Player A, and the other player, Player B. If we assign a level number of 1 to the root node and increment level numbers for a node's children by 1, then Player A's moves will be made on odd numbered levels and Player B's will be made on even numbered levels.

Not Quite Minimax

In order to use the minimax algorithm, we must have a function that rates a given Connect N scaffold (with zero or more pieces played by each player) according to the following criteria:

1. If the computer has won (i.e., has N checkers in a row), then the function yields a value of 1
2. If the human has won (i.e., has N checkers in a row), then the function yields a value of −1
3. If it's a tie game that's over (the scaffold is all filled), then the function yields a value of 0.

The diagram above shows a tic-tac-toe game tree with similar 1,0,−1 ratings representing an X-win, a tie game, and an O-win respectively.

The Minimax Algorithm

Now, let's consider pseudocode for a somewhat effective computer game playing strategy (but this is not minimax):

determineGoodComputerMove():

1. When it's the computer's turn to move, the determineGoodComputerMove function will iterate through all possible moves that it can make.
2. For each possible move the computer could make, the function will:
   1. Make the move (updating the scaffold appropriately)
   2. Use the rating function to rate the resulting scaffold after the move has been made (to see if the computer just won, etc). Remember the result of each rating (e.g., store each evaluation in a collection for later).
   3. Undo the move (removing the checker from the scaffold appropriately)
3. The function will then chose the move that results in the scaffold with the highest value (e.g., a value of 1, if possible). If there is more than one possible move with the highest rating, then the function can choose whichever of these moves is most convenient.
4. The function then returns a number indicating which move should be made on behalf of the computer, and the value that will result from this move (0, 1, or −1).

As you can see, such a function will evaluate all possible moves that the computer could make, and then will make the best move given all of the possible outcomes. In the tic-tac-toe diagram above, consider the root node. It is X's turn to move, and there are 3 possible moves that X can make. X can go in the top middle, the top right, or the bottom middle. A function could therefore iterate through each of these cases, make each move, rate the scaffold, undo the move, and then decide which move is best. In the case above, none of the possible moves immediately results in a win for X, so our algorithm could arbitrarily choose any of the possible moves.

However, look a little closer at the game tree. Notice that the first two of X's potential moves (moving in the top middle square, or the upper right square) both run the risk of losing the game for X, later down in the game tree. On the other hand, if X were to move in the bottom middle square, it would be assured that at worst it could tie, and at best it would win. Unfortunately, our simple algorithm can't see that far down the game tree, so it's not going to play a very good game.

Now let's consider a slightly more complex computer playing algorithm (the minimax algorithm, a version of which you should use for your assignment):

determineBestComputerMove():

1. When it's the computer's turn to move (i.e., the makeComputerMove function has called the determineBestComputerMove function), the determineBestComputerMove function will iterate through all possible moves that the computer can make.
2. For each possible move the computer could make, the function will:
   1. Make the move (updating the scaffold appropriately with the new checker)
   2. Use the rating function to rate the resulting scaffold after the move has been made (to see if the computer just won, it's a tie, etc.).
   3. If the rating function indicates that the computer won or the move resulted in a tie, then the function should remember the result of this move (e.g., store each evaluation in a collection for later). Otherwise, call the determineBestHumanMove function (shown below) and get its return value. Then record the result of the determineBestHumanMove function (e.g., store each evaluation in a collection for later).
   4. Undo the computer's trial move (removing the checker from the scaffold appropriately)
3. The determineBestComputerMove function will then chose the move that results in the scaffold with the maximum value (e.g., a value of 1, if possible, indicating a win for the computer player). If there is more than one possible move with the highest rating, then the function can choose whichever of these moves is most convenient.
4. The function then returns two numbers: (a) one indicating which move should be made on behalf of the computer (and the makeComputerMove function can then make that move), and (b) a number (1, 0, or −1) that indicates the best possible score that the suggested move will eventually result in.

The determineBestHumanMove function works as follows (notice how similar it is to the determineBestComputerMove function):

determineBestHumanMove():

1. The determineBestHumanMove function iterates through all possible moves that the human can make in response to the last computer trial move.
2. For each possible move the human could make (remember, this is a simulated move that the computer is trying out, not a real human player move), the function will:
   1. Make the move (updating the scaffold appropriately with the new checker)
   2. Use the rating function to rate the resulting scaffold after the move has been made (to see if the human would have just won, it's a tie, etc.).
   3. If the rating function indicates that the user just won or the move resulted in a tie, then remember the result of this move (e.g., store each evaluation in a collection for later). Otherwise, call the determineBestComputerMove function (shown above) on the current scaffold and get its return value. Then record the return value of determineBestComputerMove (e.g., store each evaluation in a collection for later).
   4. Undo the current trial move (removing the checker from the scaffold appropriately)
3. The determineBestHumanMove function will then chose the move that results in the scaffold with the minimum value (e.g. a value of −1, if possible, indicating a win for the human player). If there is more than one possible move with the lowest rating, then the function can choose whichever of these moves is most convenient. Notice that while the computer function always wants to choose the move with the highest value, the human function wants to choose the move with the lowest value, which indicates a win for the human, rather than the computer.
4. The function then returns two numbers: (a) one indicating which move would likely be made on behalf of the human, and (b) a number (1, 0, or −1) that indicates the worst possible scaffold score (from the computer's perspective) that the suggested move will eventually result in (since that's what the human would try to do).

So when our determineBestComputerMove function runs, it will enumerate and try each possible computer move given the current scaffold, then recursively apply the determineBestHumanMove function to each of its possible moves (to see what the human's response would be, etc.), and then select the move that results in the best possible score for the computer. Consider the top row of the tic-tac-toe board below. As you can see by the numbers in parentheses under the top node, the X player has three potential moves which result in scores of −1, −1 and 0. The computer knows, therefore, if it chose either of the first two moves, this would result in a loss for the computer. So the computer would choose the third move, which results in the worst case with a tie game, and in the best case with a win.

In contrast, when our determineBestHumanMove function runs, it will enumerate and try each possible human move, then recursively apply the determineBestComputerMove function to each of its possible moves (to see what the computer's response would be, etc.), and then select the move that results in the worst possible score for the computer. Consider the leftmost node on the second row of the tic-tac-toe board below. As you can see by the numbers in parentheses under this node, the O player has two potential moves that it can make. The first results in a score of 1 and the second in a score of −1. If the human were to take the first of these two moves, this would result in a win for the computer (1), so the human would not likely make that move. In contrast, if the human were to make the second move, this would result in a win for the human (−1). Since the human wants to pick the move that yields the worst result for the computer, it would select the second move (placing O in the lower center slot).

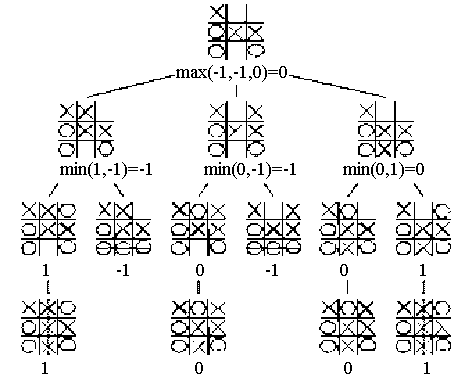
These two functions mutually call each other over and over, evaluating millions and millions of possible combinations. Each function does what's in its best interest, and reports up to the caller (the other function) what it would do in the given circumstance. At the topmost level, the determineBestComputerMove function will be provided with the summary of all this work and can then decide which move is best, and make it.

This algorithm only works when the number of potential moves to try out is small (in the case of tic-tac-toe, there are far fewer than 9! potential games that need to be played out), which is quite realistic given modern computer speeds. On the other hand, the game of chess has way too many moves to use this simple algorithm. However, an adaptation of the minimax algorithm is still used in chess playing programs.

The pseudocode above for determineBestComputerMove and determineBestHumanMove is for purposes of explanation. In fact, you don't need two separate functions, since the chooseMove function you will write takes a parameter that says whose move it is you're considering.

One problem with the minimax algorithm we've shown, as far as a natural style of play goes, is that all wins are considered equally good, and all losses are equally bad. But a natural style of play is that if I can win in one move, or, no matter what my opponent does, I can force a win in five moves, I'll prefer the quicker win. Similarly, if I'm in a position where I will lose against an opponent playing perfectly no matter what I do, I'd make a move that would delay the loss as long as possible, in the hope my opponent might make a mistake. For example, if it's Black's turn to play in this 3 by 3 game, where three in a row is needed to win

	| | | |
	| |R| |
	| |R|B|
	+-+-+-+

then if Black plays in column 1 or 3, Red wins immediately by playing in column 2. But if Black plays in column 2, then if Red plays in column 1, Red can force a win (with the game playing out as either B3 R3 or B1 R1 B3 R3, either way resulting in Red forming a diagonal three in a row). The minimax algorithm we presented would be indifferent between the three columns, since no matter which Black chooses, Red can win, so we might see Black play in column 1, missing what to an observer would be an obvious block. The better move would be in column 2. If Red then makes a mistake and plays in column 3, Black can force a draw (B3 R1 B1 R1).

So how can we fix this? All it takes is a simple modification to the rating function to weigh earlier wins more than later wins, and later losses more than earlier losses. If we pass an extra parameter that keeps track of the recursion depth (or we use a proxy for that, like the number of filled spaces in the scaffold), then we just change the value of a win from +1 to +(BIGNUMBER−depth), while a loss is worth −(BIGNUMBER−depth).

Your assignment

For this project, you will write several classes that will work together to play Connect N. We have provided you with a collection of skeleton source files to help you along: skeleton.zip. So that we can effectively test your program, we have specified some classes you must have and public functions they must implement.

Constants

You must have these constants with the specified values:

const int VACANT = -1;
const int RED = 0;
const int BLACK = 1;
const int TIE_GAME = -1;

These are so defined in the skeleton we provide you.

class Scaffold

The Scaffold class is responsible for maintaining the scaffold. A Scaffold object knows about the scaffold and the checkers. Users of the Scaffold class think of the columns in the scaffold as being numbered from left to right starting at 1; the levels are considered to be numbered from bottom to top starting at 1. Notice that this numbering is an aspect of the class's interface and our test code will depend on it. Of course, your implementations of the class's functions are free to map that numbering scheme into something more convenient for their internal use.

The Scaffold class must support these public member functions:

Scaffold(int nColumns, int nLevels);

Construct a Scaffold with the indicated number of columns and levels. If either is not positive, you may terminate the program after writing a message to cerr.

int cols() const;

Return the number of columns in the scaffold.

int levels() const;

Return the number of levels in the scaffold.

int numberEmpty() const;

Return the number of positions in the scaffold not occupied by a checker.

int checkerAt(int column, int level) const;

If there is a red checker at the indicated column and level, return RED; if there's a black checker there, return BLACK; otherwise, return VACANT.

void display() const;

Display the scaffold to the screen in the following manner:

• Display the levels of the scaffold from highest to lowest.
• Display each red checker as an R.
• Display each black checker as a B.
• Display each vacant cell as a space character.
• Display a - (hyphen) character below level 1 of each column.
• Display the side of each column as a | character.
• Display the joints between the bottom of the column and the sides of the columns as + characters.

Below is an example of the output where the scaffold has 4 columns and three rows:

	| | | | |
	| |R| | |
	|R|B|B|R|
	+-+-+-+-+

bool makeMove(int column, int color);

If the first parameter is a valid column number with at least one vacant position in that column, and if color is RED or BLACK, drop a checker of the appropriate color into that column and return true. Otherwise, do nothing and return false.

int undoMove();

Undo the most recently made move that has not already been undone (i.e., remove the checker in the scaffold that was most recently added), and return the number of the column from which that checker was removed. If there are no checkers in the scaffold, do nothing and return 0.

Here's an example:

	Scaffold s(3, 2);
	s.makeMove(2, RED);
	s.makeMove(1, BLACK);
	s.makeMove(1, RED);
	s.display();
	//  |R| | |
	//  |B|R| |
	//  +-+-+-+
	s.undoMove();
	s.display();
	//  | | | |
	//  |B|R| |
	//  +-+-+-+
	s.undoMove();
	s.display();
	//  | | | |
	//  | |R| |
	//  +-+-+-+

class Player

Player is an abstract base class that defines a common interface that all kinds of players (human and various computer players) must implement. It must support these public member functions:

Player(std::string name);

Create a Player with the indicated name.

std::string name() const;

Return the name of the player.

virtual bool isInteractive() const;

Return false if the player is a computer player. Return true if the player is human. Most kinds of players will be computer players.

virtual int chooseMove(const Scaffold& s, int N, int color) = 0;

Every concrete class derived from this class must implement this function so that if the player were to be playing the indicated color and have to make a move given scaffold s, with a goal of getting N in a row, the function returns the column the player would choose. If no move is possible, return 0.

virtual ~Player();

Since this class is designed as a base class, it should have a virtual destructor.

Each concrete class derived from Player will implement the chooseMove function in its own way. Of the classes listed here, only HumanPlayer::isInteractive should return true. (When testing, we may supply other kinds of interactive players.) Each of the three classes listed here must have a constructor taking a string representing the name of the player.

class HumanPlayer (derived from Player)

A HumanPlayer chooses its move by prompting a person running the program for a move (reprompting if necessary until the person enters a valid move), and returning that choice. You may assume that the user will enter an integer when prompted for a column number, although it might not be within the range of valid column numbers. (In other words, we won't test HumanPlayer by providing input that is not an integer when an integer is required. The techniques for dealing with the issue completely correctly are a distraction to this project.

class BadPlayer (derived from Player)

A BadPlayer is a computer player that chooses an arbitrary valid column and returns that choice. "Arbitrary" can be what you like (e.g., always the leftmost non-full column, or always the column with the fewest checkers, or a randomly selected non-full column, or whatever) provided the move is legal. The point of this class is to have an easy-to-implement class that at least plays legally.

class SmartPlayer (derived from Player)

Here's your chance to shine. A SmartPlayer chooses a valid column and returns it. A SmartPlayer will always take the opportunity to win a game, if given that opportunity, and it will never make a move that will cause it to lose or draw a game, if there is a better move available to it. A SmartPlayer prefers an earlier win to a later win. Furthermore, if a SmartPlayer determines that no matter what move it makes, it would lose to a perfect opponent, then it must chose a move that delays the loss as long as possible (giving the opponent a chance to make a mistake).

You can test your game on the SEASnet Linux server by transferring your program files and building and running an executable named, say, game:

	g32 -o game *.cpp
	./game

Once you are confident your program is correct, you are ready to verify that SmartPlayer::chooseMove meets the performance requirements detailed below. Have your main routine create a game that has at least one SmartPlayer and build your executable and run it using the following commands:

	g32fast -o game *.cpp
	./game

(You don't have to know this, but our g32fast command omits some of the runtime error checking compiler options that our g32 command supplies, and it adds the -O2 compiler option that causes the compiler to spend more time optimizing the machine language translation of your code so that it will run faster when you execute it.)

Here are the performance requirements. For any scaffold of up to the following sizes with N up to the following limits, SmartPlayer::chooseMove must return its choice in no more than ten seconds on the SEASnet Linux server cs32.seas.ucla.edu:

SmartPlayer::chooseMove is not required to work correctly if it is passed a scaffold that could not have arisen in the course of a game when it's a player's turn to move. Examples of such bad scaffolds would be one with a checker above an empty space in a column, or one where one or both players already has N checkers in a row (so the game would have already been over).

class Game

This class manages a game of a particular size by configuring the scaffold and playing the game. It must support these member functions:

Game(int nColumns, int nLevels, int N, Player* red, Player* black);

Construct a Game to be played with the indicated players on a scaffold of the indicated size. The red player always moves first. The goal of the game is for a player to get N of their checkers in a row. If N is not positive, you may terminate the program after writing a message to cerr.

bool completed(int& winner) const;

If the game isn't over (i.e., more moves are possible), return false and do not change winner. Otherwise, set winner to RED, BLACK, or TIE_GAME, reflecting the outcome of the game, and return true.

bool takeTurn();

If the game is over, return false. Otherwise, make a move for the player whose turn it is (so that it becomes the other player's turn) and return true.

void play();

Play the game. Display the progress of the game in a manner of your choosing, provided that someone looking at the screen can follow what's happening. If neither player is interactive, then to keep the display from quickly scrolling through the whole game, it would be reasonable periodically to prompt the viewer to press ENTER to continue and not proceed until ENTER is pressed. (The ignore member function for input streams is useful here.) Announce the winner at the end of the game.

int checkerAt(int column, int level) const;

In the Game's scaffold, if there is a red checker at the indicated column and level, return RED; if there's a black checker there, return BLACK; otherwise, return VACANT. This function exists so that we and you can more easily test your program; a real client would never use it.

Here's an example of a program that plays a game between a person and a bad computer player:

	int main()
	{
        	BadPlayer bp("Homer");
        	HumanPlayer hp("Marge");
		Game g(4, 3, 3, &bp, &hp);
		g.play();
	}

whereas this one is played between two computer players:

	int main()
	{
        	BadPlayer bp1("Bart");
        	BadPlayer bp2("Homer");
		Game g(4, 3, 2, &bp1, &bp2);
		g.play();
	}

Organizing the source files

To ensure that you do not change the interfaces to the required classes, we have implemented them for you. But don't get your hopes up that we're doing any significant work for you here: Our implementation is to simply give Scaffold, say, just one private data member, a pointer to an ScaffoldImpl object (which you can define however you want in Scaffold.cpp) The member functions of Scaffold simply delegate their work to functions in ScaffoldImpl. You still have to do the hard work of implementing those functions.

Instead of having one class per file, for our ease of testing, you must organize your source code in the following manner:

provided.h

We provide this file for you that defines certain constants and declares the required classes. You must not change this file in any way.

main.cpp

This file contains your main routine. It may do whatever you want; you will not be turning it in. Presumably, you would use it to test your classes.

Scaffold.cpp

Your Scaffold implementation goes here.

Player.cpp

Your HumanPlayer, BadPlayer, and SmartPlayer implementations go here.

Game.cpp

Your Game implementation goes here.

support.h (optional)

This file contains additional constants, class declarations, and the like that you want to use in more than one of the cpp files.

support.cpp (optional)

This file can be used for implementations of things that you declare in support.h.

The support files are for those additional functions that you find useful in more than one of the .cpp files. (If you wanted to use them in only one file, then just put them in that file.) You don't have to create the support files if you have no use for them. As an example, given a scaffold, both Game::takeTurn and SmartPlayer::chooseMove may want to make a move on that scaffold for a player. You could have them both call a non-member function that takes a Scaffold& parameter and uses only the public interface of Scaffold. This function's declaration would go in support.h and its implementation in support.cpp.

Other than Scaffold.cpp, no source file that you turn in may contain the name ScaffoldImpl. Thus, code in your other files must not directly instantiate or even mention ScaffoldImpl. They may use the Scaffold class that we provide (which indirectly uses your ScaffoldImpl class). Other than Player.cpp, no source file that you turn in may contain any of the names HumanPlayerImpl, BadPlayerImpl, and SmartPlayerImpl. Other than Game.cpp, no source file that you turn in may contain the name GameImpl. You may otherwise make whatever reasonable changes you like to the .cpp files that aren't otherwise forbidden by the spec: You may add data members and member functions, public and private, to the Impl classes, or add non-member helper functions not used in other files, for example.

If we create a project consisting of the files you turn in, but using the provided.h and main.cpp from the skeleton, the program must build successfully.

If we create a project consisting of the files you turn in, but using the provided.h and main.cpp from the skeleton, and replacing your Scaffold.cpp with our correct implementation that behaves as specified, the project must build successfully. For example, if a Game member function depends on there being some additional non-member function relating to Scaffold, that function can't be in Scaffold.cpp. (While stylistically it should be, for our testing purposes you'll have to put such a function in support.cpp and its declaration in support.h.)

The provisions of the preceding paragraph similarly apply if we replace your Player.cpp with ours. It also applies if we replace your Game.cpp with ours.

If we replace your Scaffold.cpp with ours as indicated above, or your Player.cpp, or your Game.cpp, your functions must still behave correctly. This implies that you can't, for example, have a global variable that a Scaffold member function looks at under the assumption that a Game member function set it a certain way. In other words, the only communication between your Scaffold, Game, and various player objects must be through the interfaces defined in provided.h.

No member function of the required classes may cause anything to be written to cout except Scaffold::display, Game::takeTurn, Game::play, and the chooseMove function of any class derived from Player for which isInteractive returns true. If you want to print things out for debugging purposes, write to cerr instead of cout. When we test your program, we will cause everything written to cerr to be discarded; we will never see that output, so you may leave those debugging output statements in your program if you wish.

No member function of the required classes may cause anything to be read from cin except Game::play and the chooseMove function of any class derived from Player for which isInteractive returns true.

During execution, your program must not perform any undefined actions, such as dereferencing a null or uninitialized pointer. Your program must not leak memory.

You will not turn in provided.h or main.cpp. When we test your program, we'll do so in a project in which we supply the same provided.h we gave you and our own testing main routine.

If the main routine we supply is the following, your program must build successfully. When the resulting executable is run, it must write

	|B| | |
	|R| | |
	+-+-+-+
	Passed all tests

and nothing more to cout, and terminate normally.

	#include "provided.h"
	#include <iostream>
	#include <cassert>
	using namespace std;

	void doScaffoldTests()
	{
	    Scaffold s(3, 2);
	    assert(s.cols() == 3  &&  s.levels() == 2  &&
                        s.numberEmpty() == 6);
	    assert(s.makeMove(1, RED));
	    assert(s.makeMove(1, BLACK));
	    assert(!s.makeMove(1, RED));
	    assert(s.numberEmpty() == 4);
	    assert(s.checkerAt(1, 1) == RED  &&  s.checkerAt(1, 2) == BLACK);
	    assert(s.checkerAt(2, 1) == VACANT);
	    s.display();
	}

	int main()
	{
	    doScaffoldTests();
	    cout << "Passed all tests" << endl;
	}

If the main routine we supply is the following, your program must build successfully. When the resulting executable is run, it must write two rows of equal signs and Passed all tests, and terminate normally. Nothing more may be written to cout except that between the two rows of equal signs, something will be written to prompt for Marge's move.

	#include "provided.h"
	#include <iostream>
	#include <cassert>
	using namespace std;

	void doPlayerTests()
	{
	    HumanPlayer hp("Marge");
	    assert(hp.name() == "Marge"  &&  hp.isInteractive());
	    BadPlayer bp("Homer");
	    assert(bp.name() == "Homer"  &&  !bp.isInteractive());
	    SmartPlayer sp("Lisa");
	    assert(sp.name() == "Lisa"  &&  !sp.isInteractive());
	    Scaffold s(3, 2);
	    s.makeMove(1, RED);
	    s.makeMove(1, BLACK);
	    cout << "=========" << endl;
	    int n = hp.chooseMove(s, 3, RED);
	    cout << "=========" << endl;
	    assert(n == 2  ||  n == 3);
	    n = bp.chooseMove(s, 3, RED);
	    assert(n == 2  ||  n == 3);
	    n = sp.chooseMove(s, 3, RED);
	    assert(n == 2  ||  n == 3);
	}

	int main()
	{
	    doPlayerTests();
	    cout << "Passed all tests" << endl;
	}

If the main routine we supply is the following, your program must build successfully. When the resulting executable is run, it must terminate normally. The last line written to cout must be Passed all tests.

	#include "provided.h"
	#include <iostream>
	#include <cassert>
	using namespace std;

	void doGameTests()
	{
	    BadPlayer bp1("Bart");
	    BadPlayer bp2("Homer");
	    Game g(2, 2, 2, &bp1, &bp2);
	    int winner;
	    assert(!g.completed(winner));
	    g.takeTurn();  // Red's first move
	    assert(!g.completed(winner)  &&
	                (g.checkerAt(1, 1) == RED  ||  g.checkerAt(2, 1) == RED));
	    g.takeTurn();  // Black's first move
	    assert(!g.completed(winner));
	    g.takeTurn();  // Red's second move; Red must win
	    assert(g.completed(winner)  &&  winner == RED);
	}

	int main()
	{
	    doGameTests();
	    cout << "Passed all tests" << endl;
	}

Turn it in

By Tuesday, May 20, there will be a link on the class webpage that will enable you to turn in your source files and report. You will turn in a zip file containing three to five source files and a report file.

• Scaffold.cpp, Player.cpp, and Game.cpp. If you used support.h, turn it in as well. If you used support.cpp, turn it in as well. Comment any function you add to indicate what it does. Comment any non-trivial code.

• report.docx (in Word format) or report.txt (an ordinary text file), a report containing

  • a description of the design of your classes. We know what the public interfaces are, but what about your implementations: What are the major data structures that you use? What additional functions did you define for what purpose?

  • a description of your design for SmartPlayer::chooseMove.

  • pseudocode for non-trivial algorithms.

  • a note about any known bugs, serious inefficiencies, or notable problems you had.

  How nice! Your report file does not have to contain any list of test cases.

Advice

The skeleton solution we give you has stub implementations for all the classes. It will build successfully, but not do anything interesting. Start by implementing the Scaffold functionality and test it. Implement and test BadPlayer next, then HumanPlayer, then Game. If you then make SmartPlayer choose a move the same way BadPlayer does, you have a working program that will be worth about two-thirds of the correctness points.

After this works perfectly, try to earn the rest of the correctness points by making SmartPlayer choose its moves intelligently. No matter how intelligently you try to make SmartPlayer play, it won't earn any of these points if it ever chooses an illegal move.

To speed up your program for larger scaffolds, you can build your program in the Release configuration instead of the Debug configuration. Programs built in the Release configuration run much faster than in the Debug configuration, but you lose the ability to get much information from the debugger if you're using it to track down a bug. (You can always switch the configuration back from Release to Debug if you like.) When we test your program, we will build it in the Release configuration. Here's how you do that in Visual C++:

1. At the top of main.cpp (outside of the main function), add the lines

   	#if defined(_WIN32) || defined(_WIN64)
   	#include <iostream>
   	#include <windows.h>
   	#include <conio.h>
   
   	struct KeepWindowOpenUntilDismissed
   	{
   	    ~KeepWindowOpenUntilDismissed()
   	    {
   	        DWORD pids[1];
   	        if (GetConsoleProcessList(pids, 1) == 1)
   	        {
   	            std::cout << "Press any key to close this window . . . ";
   	            _getch();
   	        }
   	    }
   	} keepWindowOpenUntilDismissed;
   	#endif
   

   (You can leave these lines in even if you go back to running in Debug mode or run under g++.)

2. In the Build menu, select Configuration Manager.

3. In the drop-down list under Active Solution Configuration, select Release instead of Debug, and then close that dialog.

Caution for Visual C++ users: In Release mode, Visual C++ ignores assert statements during execution. The expression in an assertion is not evaluated. This means that if that expression has a side effect, that side effect will not happen (e.g., if the expression says to call a function that changes something, that function will not be called, so the something is unchanged). It also means that if the expression would have evaluated to false if it had been executed, terminating your program, what will happen instead is that your program just continues on as if the assert statement were not there. This caution does not apply to clang, g++, or g32fast users: For these compilers, building in Release mode or with optimizations turned on does not affect how assert statements behave.

Under Xcode, to turn on optimization, select Project / Scheme / Edit Scheme... / Run / the Info tab / Build Configuration / Release.

Under Linux, the -O2 to the g++ command turns on optimization; for example, to produce an optimized executable named game:

	g++ -O2 -o game *.cpp

On a SEASnet Linux server, you can use our g32fast command:

	g32fast -o game *.cpp