Connectionist Natural Language Processing:
A Status Report
Michael G. Dyer
Computer Science Department
UCLA, Los Angeles, CA 90024
Abstract
Natural language processing requires high-level symbolic capabilities, including: (a) the creation and propagation of dynamic bindings, (b) the manipulation of recursive, constituent structures, (c) the acquisition and access of lexical, semantic, and episodic memories, (d) the control of multiple learning/processing modules and the routing of information among modules, (e) the "grounding" of basic-level language constructs (e.g. objects, actions) in perceptual/motor experiences, and (f) the representation of abstract concepts. In this paper we examine the state-of-the-art techniques in connectionist modeling to support such capabilities for natural language processing, along with their current strengths and weaknesses.
1. Introduction
Connectionist networks (CNs) exhibit many useful properties. Their spreading activation processes are inherently parallel in nature and support associative retrieval of memories. The summation and thresholding of activation allows for smooth integration of multiple sources of knowledge. CNs with distributed representations (Rumelhart and McClelland 1986) exhibit robustness in the face of noise/damage and can learn to perform complex mapping tasks just from examples. Connectionist networks are also able to dynamically reinterpret situations as new inputs are received. These features are very useful for natural language processing (NLP) and offer the hope that connectionist approaches to NLP will replace the more traditional, symbolic approaches to NLP.
Consider the task of lexical disambiguation. Words may have multiple meanings, for instance, "pot" may refer to a cooking pot, a flower pot, or marijuana. Traditional, symbolic approaches to disambiguation have utilized one of the following strategies: (a) commit to a particular interpretation and then backtrack if it is later shown to be incorrect, (b) delay the process of disambiguation until enough information is gathered so that backtracking will not occur, (c) keep track of every possible meaning, or (d) commit to an interpretation and later execute error-correction heuristics if that interpretation is shown to be wrong. None of these strategies is completely adequate. The commit-and-backtrack strategy is very inefficient, because backtracking will often cause much useful work to be thrown away. For instance, assume that the cooking-pot meaning of "pot" is first chosen while reading sentence S1 and then subsequent information in the sentence leads to a marijuana interpretation of "pot".
S1: The pot, which Mary bought from John, made her cough.
Here, backtracking to reinterpret "pot" (after encountering "cough") will cause the perfectly adequate analysis of the intervening relative clause to be thrown away and then redone.
The delay strategy has the following general problems: (a) the analysis of the rest of the sentence may not be able to go forward while commitment to a meaning is delayed and (b) no matter how long disambiguation is delayed, subsequent input may cause a reinterpretation of a given word to occur anyway -- e.g., as would occur if S2 followed S1:
S2: Mary was allergic to the flower in it.
The every-possible meaning strategy suffers from a potential combinatorial explosion of interpretations. If there are n k-way ambiguous words in a segment of text then there will be k
n possible interpretations of that text. The intelligent error-correction strategy requires the specification of rules to selectively undo the harm caused by earlier commitments. As these rules execute, they will cause other inferences to be undone, which will cause yet other error-correction rules to execute, and so on. This approach requires either designing sophisticated error-correction heuristics or some kind of a general truth maintenance mechanism.In contrast, dynamic reinterpretation is achieved as a natural side-effect of how connectionist networks operate. Activation spreads in parallel and the nodes with the most activation represent the current interpretation. As new inputs are received, the most highly active nodes may drop in activation, leading to a reinterpretation of prior inputs. Initially, the cooking-pot node will have the most activation, but "cough" will cause the marijuana node to become more active (through an activation path of smoking, etc.). Subsequent mention of being allergic will send more activation to nodes representing a different reason for coughing and, along with "flower", cause the flower-pot interpretation now to be most preferred. Thus, spreading activation exhibits aspects of all of the traditional strategies, but is implemented via a single, uniform, parallel and efficient mechanism.
The long-term goal of connectionist researchers is the complete replacement of symbolic processing models with connectionist models that exhibit efficient, robust performance and are capable of automatically learning all of the tasks that are currently programmed directly by knowledge engineers within the field of artificial intelligence. Given the many known attractive features of connectionist networks, why hasn't the connectionist paradigm already swept aside the traditional, symbolic approach? The answer lies in the fact that the symbolic processing approach retains its own attractive representational and processing features. Connectionist models, while becoming ever more powerful and sophisticated, have not yet been able to provide equivalent (let alone alternative superior) capabilities to those exhibited by symbolic systems. The rest of this paper consists of an enumeration of these symbolic capabilities, along with a description of how current connectionist networks (both localist and distributed) attempt to simulate these capabilities, and with what success (or failure).
2. Dynamic Bindings
Symbolic systems are capable of binding variables to values at run time. In symbolic systems, values may range from simple entities to complex recursive structures of arbitrary depth. Let us first consider bindings to simple (i.e. unstructured) values. For instance, the knowledge that we own what we buy might be represented by a rule something like R1:
R1: BUYS(person1, object, person2) ====> OWNS(person2, object)
This rule will work for any object or person, as a result of the (typed) variables person1, object and person2 being bound to their appropriate values at execution time.
2.1. Bindings in Localist CNs
In localist CNs, each node represents a given syntactic or semantic entity (e.g. a predicate, such as OWNS, or a role, such as BUYER) and the amount of activation on the node represents how committed the network is to a given node (or path of nodes) as the correct interpretation of the input. However, without some kind of variable+binding mechanism, localist CNs would have to represent, before execution, all possible binding combinations, which would lead to a combinatorial explosion. For instance, for a network to conclude that Mary owns a tv (or, say, a radio) because she bought it from another person (say, Fred or Joe), then there would already have to exist CN nodes for: MARY-OWNS-TV, FRED-OWNS-TV, MARY-OWN-RADIO, etc. For just n characters and m buyable objects, there would be nxm OWNS nodes alone and an exponential number of mappings from BUYS to OWNS structures. To avoid this problem, current localist CNs use either signatures or phase synchronization to propagate simple bindings.
(1) Signatures: A signature is a unique activation value that is assigned to a given entity and that serves as a value in a binding. For instance, the CN node representing FRED might be assigned an activation value of 23 as its permanent, identifying activation (or signature) while Mary is assigned 13 and TV is assigned, say, an activation value of 7 as its signature. Signature activation is then propagated in the network along separate pathways from those used for normal spreading activation. To represent rule R1, nodes are assigned to each predicate (OWNS, BUYS) and to each role (i.e. BUYS:BUYER, BUYS:SELLER, BUYS:OBJECT, OWNS:OWNER and OWNS:OBJECT) and connections are set up between roles (e.g. from BUYS:BUYER to OWNS:OWNER) to specify how bindings should be propagated between predicates. Normal activation is propagated from BUYS to OWNS to represent a commitment to the fact that OWNS has occurred as the result of a BUYS. At the same time, signatures are propagated along role-to-role pathways. The weights on these pathways are normally set to 1 so that the values of the signatures are not altered. If the signature, say, 23 spreads from BUYS:BUYER to OWNS:OWNER and the signature 13 spreads from BUYS:OBJECT to OWNS:OBJECT, then the network can be interpreted as inferring that FRED's buying a TV resulted in FRED owning a TV. Lange and Dyer (1989) and Sun (1989, 1992, 1993) have both designed systems that make use of signature-style activation to propagate simple role-bindings.
(2) Phase synchronization: In this approach, the unit time for each basic spread-of-activation step is broken up into a few, smaller subunits of time, termed phases. For instance, if there are seven distinct phases within each spread-of-activation step, then a total of seven distinct bindings can be propagated through a localist network. In the example above, FRED, MARY and TV might be assigned phases 1, 4, and 7, respectively. The nodes in such networks are designed so that, when they receive activation within a given phase, they propagate it along their connections within the same phase of the next basic spreading-activation cycle. Phase-locking (or synchronization) was originally proposed by neuroscientists (von der Malsburg 1981; von der Malsburg and Singer 1987) and has been employed by vision researchers to bind distinct features (e.g. color and shape) when more than one object is in the visual field (Strong and Whitehead 1989). Shastri and Ajjanagadde (1990, 1993) (Ajjanagadde and Shastri 1989) make use of phase-locking to propagate bindings in a localist CN used to perform deductive retrieval of information.
The signature approach has the advantage that an unbounded number of signatures can be propagated simultaneously along multiple pathways while the phase-locking method is restricted to a small number of bindings. The restriction to just a few phases is not a problem for retrieval tasks, which rarely specify more than 7 unbound variables in a query. However, during natural language understanding, many new bindings can arise dynamically. For instance, within sentence S3 there are over 10 bindings that arise.
S3: The tall, thin woman bought an expensive, red sports car from the bald salesman.
Also, for n phases there are n subcycles required for each spread of activation cycle, which slows down propagation rates by a factor of n. However, both phase-locking and signature approaches suffer from the fact that only simple values can be propagated. Consider the following, common rule -- one that is ubiquitous in story understanding systems:
R2: TELLS(person1, message, person2) ===> KNOWS(person2, message)
The difference between R1 and R2 is that a message can be bound to any arbitrarily complex structure. For instance, if John tells Mary that a purple alien stole the hubcaps off her car, then a story understanding system should update Mary's knowledge to know this complex fact/event. In symbolic systems, this update feat is simple because all that has to be passed between TELLS and KNOWS is a pointer to the instantiated STOLE structure, say STOLE3. The STOLE3 instance will have its roles bound (i.e., that the alien is the STOLE:STEALER and the hubcaps are the STOLE:OBJECTS, etc.) as the result of parsing/analysis of the stole-related part of the text. But what would be the signature (or phase) for such a complex entity? If a STOLE3 node already exits in the network, with a unique signature preassigned, then this signature can be propagated from TELLS to KNOWS. However, in most cases the message is being mentioned for the first time by a story character; so the story understanding system must infer KNOWS from TELLS at about the same time that the stole event itself is being comprehended and incorporated into memory. Thus, any connectionist NLP system must face the problem of both dynamically creating instances of structured entities and propagating them for inferencing (e.g., so that the system can infer that Mary will be upset, etc.).
The 'solution' of allowing the dynamic creation of new connectionist nodes and links at run time is not acceptable within the connectionist paradigm because it violates known constraints from neuroscience. New neurons, axons or dendrites simply cannot grow within the moments that pass during the comprehension of a sentence. Also, symbolic pointers are not acceptable because they refer to the location of a memory register and there is no evidence that any pattern of activation in one area of the brain directly encodes the location (address) of some other area in brain (as occurs with a von Neumann-style pointer.)
2.2. Bindings in Distributed CNs
Given that new nodes and connections cannot be created "on the fly" in CNs, structured bindings must be created dynamically either by modification of fast synapses (modeled as connection weights in CNs) or by changes in patterns (i.e. entire vectors) of activation over ensembles of connectionist units. Distributed CNs offer such a potential, since they manipulate patterns of activation over banks of connectionist processing units. The use of distributed patterns supports the dynamic creation of a potentially exponential number of possible values. Currently, two major methods have been developed for representing and propagating distributed patterns of activation as role bindings: tensor products and ID+Content vectors.
(1) Tensor Products: Tensor theory has been proposed for use in CNs by Smolensky (1990) and implemented in (Dolan 1989; Dolan and Dyer 1989; Dolan and Smolensky 1989). Tensors result when vectors are generalized to higher ranks (i.e., a rank-one tensor is a vector; a rank-two tensor is a matrix; a rank-three tensor is a cube of units, etc.). Suppose an m-dimensional vector V represents, say, a role R, and an n-dimensional vector W represents the role's filler F. Then R and F can be bound to one another by generating the vector outer product VW, which consists of a tensor T (in this case, a matrix) of mxn elements (i. e., element-wise products of each V
i x Wj = Tij). To extract, for instance, the binding from the role, we perform an inverse operation, such as calculating the dot (or inner) product T•W. This approach is not as straightforward as it sounds, because a single tensor product representation will contain multiple bindings overlaid on one another. For example, to represent BUYS(JOHN, TV, FRED) and OWNS(FRED, TV) we would set up a rank-three tensor (i. e. a cube of CN units) and overlay the following binding-triples:[BUYS, ACTOR, JOHN]
[BUYS, OBJECT, TV]
[BUYS, FROM, FRED]
[OWNS, ACTOR, FRED]
[OWNS, OBJECT, TV]
Here, each dimension of the cube (i.e. position in a triple) represents a predicate, a role, or a role-filler. Cross-talk will result because these multiple, rank-three outer products have been overlaid (e.g., through element-wise summation) within the same tensor product. Dolan (1989) has developed various methods for extracting bindings from tensor networks in the face of such cross-talk. For example, one method is the use of "clean-up circuits". One kind of clean-up circuit consists of a network of pre-known bindings organized via inhibition. Thus, the noisy output from the tensor product is mapped to the closest matching vector (from a fixed set of possible alternatives) via a winner-take-all process. Another method is termed "pass-thru circuits". A path-thru circuit basically applies additional dot-products (representing additional constraints on what the output should look like). For example, if we are looking for the OBJECT bought and know that it is also owned, then we can set up pass-thru circuits that essentially find the intersection of two related queries, such as [BUYS1, OBJECT, ?] and [OWNS, OBJECT, ?].
Tensors are mathematically elegant and can be implemented in a CN network via conjunctive coding -- i. e., multiplicative connections (Hinton et al. 1986). However, the problems of scale-up and cross-talk can be problematic. For n-dimensional vectors one needs n
3 units to hold bindings as [predicate, role-name, role-filler] triples. If there are numerous BUYS events, then there will be massive cross-talk or one must encode triples that distinguish instances:[BUYS1, ACTOR, JOHN]...
[BUYS2, ACTOR, JOE]
[BUYS1, ISA, BUYS]
[BUYS2, ISA, BUYS].
The problem with this approach is that, ironically, the tensor network functions so much like a symbolic system that the nice features of distributed CNs (e.g. generalization) can become lost. Also, storing and access via one triple at a time creates a system that, while parallel at the subsymbolic level, is essentially sequential at the knowledge level (Sumida and Dyer 1989; Feldman 1989) because only one triple can be accessed or manipulated at a time. In contrast, numerous triples are activated simultaneously in a localist CN, since the predicates and roles of each event are separately represented.
(2) ID+Content Vectors: In localist CNs, each instance (e.g. BUY3) is represented by a separate node, with a connection to the general type (e.g. BUY). In distributed CNs, BUY3 will consist of a pattern (i.e. vector) of activation with segments of the pattern sharing similar activation values with the activation vector representing the type. In the ID+Content approach (Miikkulainen and Dyer 1991), the vector is split up into two segments: (a) the Content segment, which holds information concerning the general type of object/action being represented and (b) the ID segment, which holds information concerning the specific instance. A distributed CN, such as a PDP network (Rumelhart and McClelland 1986), can then be trained to propagate the ID segment from one layer to another without altering the ID segment. This is accomplished by training the network on a random subset of ID patterns. Miikkulainen and Dyer (1991) have shown that PDP networks can efficiently learn to propagate novel ID patterns when trained on just a small subset of random patterns. The networks essentially learn the identity mapping for the ID segments. Miikkulainen and Dyer use this technique in the propagation of role bindings. Their system, DISPAR, contains 4 recurrent PDP networks, such as those developed by (Elman 1990), that are connected to a lexical memory. DISPAR has the task of learning to generate complete paraphrases from fragmentary inputs of novel script-based stories (Schank and Abelson 1977; Dyer et al. 1987). For instance, given the input fragment: "Mary ordered steak at Leone's." DISPAR generates a complete sequence of events -- e. g., that includes: "Mary ate steak." Thus, generating paraphrases requires propagating bindings, since DISPAR must learn (from the training data) to perform the equivalent of inferring:
ORDER(diner, food) ===> EATS(diner, food)
A problem they encountered was that long-term knowledge (implicit in the training set of script-based stories) would be encoded in the connection weights and result in short-term information (from the input story) being overridden. For example, if every story in the training set had Mary order and eat a steak at a restaurant, then, even if (during performance) the input story contained the sentence "Mary ordered a hamburger.", DISPAR would still generate "Mary ate a steak" as part of its paraphrase. This effect was also noticed in (St. John and McClelland 1990). This problem was solved in DISPAR by representing "steak" and "hamburger" each as ID+Content vectors. The Content segment of each food-type of word contained a pattern that was similar for all foods used in the training data, while the ID segments were assigned unique patterns for each distinct food instance (e.g. hamburger vs. steak). Thus, when "Mary ordered hamburger." was input during performance, DISPAR passed the ID portion to subsequent banks without alteration. DISPAR used the pattern within the Content part (i.e. the FOOD type) to aid in processing while propagating the instance (ID segment) without change. As a result, DISPAR could conclude that "Mary ate hamburger." when told "Mary ordered hamburger." even though all training set instances consisted of Mary always ordering and eating "steak".
3. Functional Bindings and Structured Pattern Matching
Although the above techniques (e.g. signatures, ID+Content vectors, etc.) have greatly extended the symbolic capabilities of both localist and distributed CNs, they are still weak when compared to the binding capabilities of symbolic systems. The use of a heap, addressing, and pointers allows symbolic systems to create structures like STOLE3 "on the fly". Symbolic systems support propagation of even more complex bindings; for instance, they allow modules to receive entire functions or procedures as data. This results in styles of programming termed "data-driven" and "object-oriented". A simple example of this capability is the APPLY function in LISP, in which one function F1 applies whatever function F2 is passed to F1 as a parameter. This code-binding and propagation capability allows one module within a symbolic system to perform any of the operations that another module is capable of.
In addition, symbolic systems typically exhibit powerful pattern matching capabilities. A prime example is that of unification, e.g. as in Prolog. Holldobler (1990) and Stolcke (1989) have built localist CNs to perform this unification process. Holldobler, for instance, sets up several layers of threshold units. The term layer is a matrix of units with one side representing the terms in two expressions to be unified and the other side representing positions where terms may occur. The unification layer contains units that are connected in a manner to impose unification constraints, for instance, whether two occurrences share a common variable. The occur check layer makes sure that cycles do not occur, such as x becoming bound to f(x).
The major problems with this localist CN approach to unification are: (a) that all of the units and their connections must be prewired for the given expressions that are to be unified and thus are finite and non-general, and (b) only a single solution is produced. In contrast, unification in logic programming languages, such as Prolog, work on an infinite number of possible expressions to be unified and can return multiple solutions when they exist. Thus, a localist CN with any generality would require a method for recruiting and wiring up units dynamically. In the area of distributed CNs there are no architectures, to my knowledge, designed to attempt unification.
4. Encoding and Accessing Recursive Structures
Recursive structure is essential for high-level reasoning, particularly natural language processing. Localist networks can represent recursive structures by connecting up the appropriate nodes in a tree-like manner. However, localist networks that propagate phases or signatures have difficulty with propagating multiple instances of the same type. Consider sentence S4:
S4: John told Mary that Betty told Fred that Jim went home.
Here there are two TELL structures. In localist CNs, there is usually only one node for each type of predicate. Thus, the "John told Mary" segment can be represented by passing signatures (or phases) over the TELL:TELLER and TELL:RECEIVER nodes. However, the embedded "Betty told Fred" must be represented by another TELL instance that would be dynamically bound to the TELL:MESSAGE node of the top-level TELL. One solution to the problem (of multiple instances of the same type) is to have n copies for each predicate (and corresponding roles). If n = 2, then the CN network could parse and represent one TELL instance embedded within another TELL. For instance, if each TELL node had a pre-assigned signature, then the signature of the embedded TELL could by propagated to the TELL:MESSAGE of the outer TELL. This approach will always fail for sentences with embeddings greater than n. This limit, on depth of recursion, may not be so bad, however, because people also exhibit a limit. Consider S5:
S5: John told Mary that Betty told Fred that Sally told Frank that Jim went home.
Most people, upon hearing such a sentence out loud, protest that they cannot keep straight who is telling whom and immediately recall it as "Several people telling other people that Jim went home.".
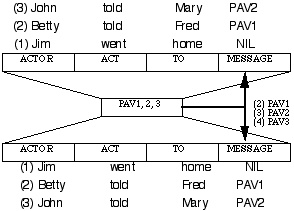
In the area of distributed CNs, early PDP networks lacked a recurrent layer; as a result, the encoding of recursive structure was problematic. If a 3-layer PDP network, for instance, had 4 banks (e.g. representing the ACT, ACTOR, RECIPIENT, OBJECT) then a sentence like S4 could not be encoded, because the embedded TELL required its own ACT, ACTOR, etc. This problem has been solved by the use of distributed CNs with a recurrent layer. A number of distinct recurrent architectures have been employed to encode recursive structures and their constituents. Two common approaches are the Simple Recurrent Network (SRN) of Elman (1990) and the Recursive Autoassociative Memory (RAAM) of Pollack (1988, 1989, 1990). In SRNs, the hidden layer is copied onto an added bank in the input layer (termed the "context" bank) and then is fed back into the hidden layer at the next cycle. In contrast, RAAMs make use of an autoassociative (or encoder) network, in which a PDP network is trained to generate on the output layer the same pattern as that placed on the input layer (Rumelhart and McClelland 1986). In Pollack's RAAMs, the pattern of activation produced on the hidden layer is copied back into a bank on both the input and output layers. Figure 1 illustrates how S4 can be encoded in a RAAM.

Figure 1. Encoding of an embedded structure within a RAAM.
First, "Jim went home" is autoassociated on the RAAM's input/output layers. The resulting pattern of activation (PAV1) in the hidden layer is then placed in the input/output banks representing the MESSAGE role. Then "Betty told Fred PAV1" is autoassociated. The resulting pattern over the hidden layer (PAV2) is placed in the MESSAGE bank. Now "John told Mary PAV2" is autoassociated. The resulting hidden-layer activation vector (PAV3) now encodes the entire recursive structure. To retrieve this recursive structure, one can place PAV3 on the hidden layer of the same RAAM and [JOHN TOLD MARY PAV2] will be reconstructed on the 4 banks of the output layer. Now PAV2 can then be placed over the hidden layer and [BETTY TOLD FRED PAV1] will be reconstructed on the output layer. When PAV1 is placed over the hidden layer, the pattern for [JIM WENT HOME NIL] will appear in the banks on the output layer. So a RAAM can basically function as a stack thus can encode both simple lists and trees into a fixed-width vector. For example, Miikkulainen (in press) makes use of a RAAM to act as a stack in a distributed CN that learns to parse embedded relative clauses.
If a long-term memory is added, to store these hidden-layer patterns (e.g. PAV1,.PAV2), then autoassociative networks can be used to store graphs (i.e. recursive structures with cycles). For instance, Dyer et al. (1992) made use of an architecture called DUAL, which consists of a 3-layer PDP network (labelled STM) and an autoassociative encoder network (labelled LTM) whose hidden layer is of the same length as the input/output layers of the STM and whose input/output layers are of a length equal to the number of weights in all STM layers. DUAL has been used to encode a simple semantic network (i.e. a graph of nodes and labelled links, with cycles). For instance, each node is defined as a number of labelled-arc-to-node pairs:
JOHN: --LOVES--> MARY
--GENDER--> MALE
--JOB--> PROFESSOR
... ...
The STM's weights are set (via backpropagation learning) to associate roles with values (e.g. LOVES on input layer and MARY on the output layer). After learning, all of the weights in the STM network are then passed as a single, (larger dimensional) vector of activation values (call it V-JOHN) to the input and output layers of LTM, which is taught to autoassociate it. Thus, LTM stores entire STM networks. To retrieve the V-JOHN STM weights, one places V-JOHN on the LTM's hidden layer. The resulting weights (on LTM's output layer) can then be used to reset the weights of the STM. To retrieve any piece of information about JOHN, we now place the appropriate role representation (e.g. JOB) on the STM input layer and its value (e.g. PROFESSOR) will appear on the output layer. Now, consider the encoding of cycles. Suppose that MARY has the following arcs:
MARY: --LOVES--> JOHN
--GENDER--> FEMALE
--JOB--> DEAN
Here we have a cycle because both [JOHN --LOVES--> MARY] and [MARY --LOVES--> JOHN]. To train STM to encode MARY, we train STM to associate MARY's roles with the appropriate values. For instance, we place LOVES on the STM input layer and V-JOHN on the STM output layer. After training, the resulting STM weights (call it V-MARY) now encode all information about MARY. However, when the JOHN network was encoded, we did not have V-MARY as the representation for MARY (we had just whatever initial, arbitrary representation had been selected to represent MARY). So now we have to retrain the JOHN STM network to properly associate LOVES with V-MARY. This encoding cycle will alter the STM weights (that encode all properties for JOHN), resulting in a new set of weights (call this vector of weights V-JOHN1). As a result, the encoding for MARY must be altered (since MARY now --LOVES---> V-JOHN1, not V-JOHN). MARY is also now better represented by a new vector (call it V-MARY1), and so on. Over time, the network will find an encoding of both JOHN and MARY as their distributed representations are recirculated through the DUAL architecture. If two nodes N1 and N2 have similar arc/node associations, then N1 and N2 will end up being represented by vectors that are very similar. This similarity aids in generalization. For instance, if a country C1 has n properties (where, say, one property is [C1: --PRODUCES--> RICE] and country C2 has n-1 properties that are the same as those of C1 (but it is not known whether or not C2 produces rice) then the similarity of the vectors formed for C1 and C2 will cause DUAL to conclude that C2 also produces rice.
5. Forming Lexical Memories
Natural language processing requires a lexical memory. In symbolic systems, each word is encoded as a symbol (e.g. in ASCII) that is mapped to some frame-like structure (Minsky 1985) with attached rules. For example, in the BORIS story understanding and question-answering system (Dyer 1983), the word "eats" is mapped to an INGEST frame with a number of rules (implemented as test/action "demons"). For instance, one of the demons searches for a FOOD frame following the INGEST frame and if found, the demon binds the FOOD frame to the OBJECT role of the INGEST frame. Another demon searches for an animate agent preceding the INGESTS frame and binds it to the ACTOR role, and so on.
In such a system, the internal (ASCII) representation for the word "eats" is arbitrary and static. In localist CNs, the node for "eats" is also static and its connections (to other nodes representing words or frames) are specified by the knowledge engineer. In contrast, in some recent distributed CN architectures, methods have been developed to automatically form distributed representations (i.e. activation vectors) for lexical entries. The most interesting and useful result of these methods is that words with similar semantics end up possessing very similar representations (e.g. as result in the recirculation method in DUAL) -- thus supporting generalization to novel yet related natural language texts. For instance, if "pasta" ends up forming a similar representation to "spaghetti" then a distributed connectionist network trained on "John ate the spaghetti" will automatically tend to correctly process "John ate the pasta" even if it has never been trained on this particular input.
Two methods have been developed for automatically forming lexical representations: Miikkulainen's FGREP method (Miikkulainen and Dyer 1991; Miikkulainen 1993) and Lee's xRAAM method (Lee 1991; Lee et al. 1990; Lee and Dyer in press). In the FGREP method, one PDP network (call it M1) is trained to map words (represented as activation vectors) or word sequences (if the network is recurrent) from banks in the input layer to banks in output layer. For instance, "chicken" might map from the SUBJECT input bank to the ACTOR output bank in "The chicken ate the worm." while it might map from the DIECT-OBJECT input bank to the RECIPIENT output bank in "The man ate the chicken." While the weights in the M network are updated (via backpropagation) to learn the correct mapping, at the same time, the vector (representing "chicken") is modified. This modification is accomplished by extending backpropagation learning over a set of weights representing "chicken" in a lexical memory. All other weights (representing other words) in the lexicon are not modified. As a result, the representation of any word W will become altered as the network M is trained to map a word W from its input to output layers. A single lexicon can then be linked to multiple PDP networks. As each network learns to map words from the lexicon, those words will be altered and their altered weight vectors are stored back into the lexicon. Thus, as each network as trained on lexical data, the representations of the training data are themselves undergoing alteration. Figure 2 illustrates the FGREP process on a recurrent network.
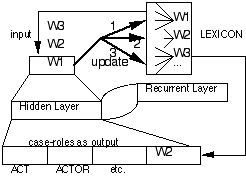
Figure 2. FGREP process. Word representations are taken from the lexicon and used to train the input/output layers of a recurrent network. During learning, backpropagation is extended back into just that section of the lexicon that represents the current input word and just its weights are updated at that point. The altered representations in the lexicon can also be used to train other networks, which will cause these words to again undergo modification.
Interestingly, convergence to stable patterns does not take much longer than training with static data. The reason is that the alterations in the representations of the lexical data make the mapping tasks easier -- i.e. for the networks that are learning to map this data from their input to output layers. That is, the network M has an easier learning task because the data being used is being altered to support M's mapping task. Using FGREP and ID+Content vectors, Miikkulainen and Dyer (1991) designed DISPAR, a story paraphrasing system consisting of 4 SRN modules and a lexical memory. Each module performs a distinct task: (a) mapping a sequence of words to a case-role event representation, (b) mapping a sequence of events to a script representation, (c) mapping a script back to an event sequence, and (d) mapping an event to a sequence of words. During training, each module is trained with word representations taken from the lexicon and modified via the FGREP method. During performance, DISPAR is given, as input, a script-based story fragment and generates, as output, a complete story -- i.e. with all intervening actions and roles instantiated.
In the xRAAM method (Lee 1991; Lee et al. 1990; Dyer and Lee in press), a distributed representation of each word is formed by encoding all propositional information in which the word is involved. An xRAAM network is a RAAM augmented with a lexical memory. Consider the word "milk". This word might be represented in terms of the following (simplified) propositions:
[MILK IS WHITE]
[MILK PRODUCED-BY COWS]
[MILK CONTAINED-IN CARTONS] ...
As each proposition is autoassociated within a RAAM (as described earlier), a pattern of activation is formed on the hidden layer. The final pattern formed is taken to be the representation of the word/symbol being encoded (in this case, MILK). By cycling back through the RAAM, this propositional information can be extracted (as described earlier for autoassociative networks). This distributed representation (i.e. as an activation vector) is stored in a separate lexicon. The representations for other words are formed in the same way. For example, COW will be involved in the following propositions:
[COW PRODUCES MILK]
[COW EATS GRASS]
[COW HAS FOUR-LEGS] ...
After COW is encoded in a RAAM and its lexical representation has been formed, we must then go back and re-encode MILK (because when [MILK PRODUCED-BY COWS] was encoded into the RAAM, the representation for COWS was different). Thus, the encoding process involves a recirculation of all words (as in the DUAL and FGREP methods) in which the fact that there are changing lexical representations cause other modules to have to be retrained on these new lexical representations (Dyer 1990). Lee terms the resulting representations Distributed Semantic Representations (DSRs) because: (a) they are distributed patterns that can be passed to a variety of CNs, (b) they encode the propositional content of the words and this content can be extracted by different modules (who were not necessarily involved in the learning of the word's representation), and (c) this "symbol recirculation" process (Dyer 1990) results in DSRs with similar meaning having similar vectors (as with the FGREP and DUAL methods). Using DSRs, Lee designed the DYNASTY system (Lee 1991; Dyer and Lee in press) -- a multi-modular system of PDP networks, SRNs, and xRAAMs -- which takes simple goal/plan-based stories as input and generates, as output, a chain of inferred goals, plans and/or sub-goal preconditions as an explanation for actions taken by the main narrative character.
6. Forming Semantic and Episodic Memories
Episodic memory (Tulving 1972) consists of personal episodes or events and is distinct from semantic memory, which consists of general world knowledge. In symbolic systems, both semantic and episodic memories are built out of symbols. The knowledge engineer selects the basic set of symbols to use. Episodic memory then consists of instantiations of semantic memory symbols. For instance, semantic memory in the BORIS system (Dyer 1983) contained an INGEST structure in semantic memory. Specific INGEST instances were indexed in episodic memory as the result of reading a story involving a particular character eating a particular food at some particular location or time.
In localist CNs, semantic memory consists of a connected network of nodes, also specified by the knowledge engineer. The formation of episodic memories is problematic in localist CNs because any dynamically-created instance is represented by semantic nodes momentarily containing signature (or phase-locked) activation. This activation must be cleared from the network before the next sentence is read. But then how are any event instances to be stored away for long-term retrieval? One way is to simply created new nodes and links, but as we have seen, this approach violates a connectionist paradigm constraint. Thus, any localist CN theory of episodic memory will require a theory of how to "recruit" preexisting nodes and connections to form new, long-term memories.
In distributed CNs, the formation of semantic memories is straightforward. Semantic memory is represented in the weights of the network. These weights undergo modified (e.g. via backpropagation) to reflect statistical features inherent in the training data. However, the storage and retrieval of specific episodes is problematic because events are laid on top of one another in a distributed connectionist network (since the same network performs multiple mappings). This approach supports generalization but makes the retrieval of individual events difficult. To date, the most successful approach to modeling episodic memory has been to make use of extensions of Kohonen self-organizing feature maps (Kohonen 1988). A feature map consist of a 2-dimensional plane of units, with each unit receiving, in parallel, the same n-dimension vector as input along its weights. The most active unit on the map then causes its neighboring units to modify their weight vectors so that, in the future, they will respond more to that input. The result of this form of learning is that similar inputs will tend to activate contiguous regions. Thus, a Kohonen feature map clusters or self-organizes the input data in a 2-D space without the need for explicit training (as in backpropagation). Feature maps have several nice properties, including: (a) Similar events will be stored in similar regions, thus supporting generalization. (b) Distinct vectors will be mapped to different regions and thus be retrieved without interference from other memories. In general, humans recall very distinct actions/objects more easily also. (c) Recent memories get laid on top of other and thus are more memorable. Humans also demonstrate this kind of recency effect.
The DISCERN system (Miikkulainen 1993) is an extension to DISPAR that includes a question-answering module that learns to retrieve unique events from an episodic memory. The episodic memory consists of Kohonen features maps that are organized into a 3-level hierarchy. At the top level, different scripts are self-organized on the map (e.g. restaurant vs. travel vs. shopping). At the middle level are maps that self-organize distinct tracks within a given scripts (e.g. for restaurants, the tracks are fastfood vs. cafeteria vs. snazzy restaurant, etc.). At the bottom level are the unique bindings (e.g. within the fastfood track of the restaurant script, the diner was Joe and the food was steak). Hierarchical maps were employed to speed up learning because, in Miikkulainen's task domain, the data itself is hierarchical. Another extension Miikkulainen made was to alter feature maps so that they could store bindings. Standard Kohonen maps simply categorize their data. Miikkulainen altered the bottom level feature maps so that role bindings are encoded in the lateral connections (i.e. between nearby units on the map).
How does this approach compare to that use in symbolic systems? Kolodner (1984) developed a symbolic, computational model of human episodic memory. Her system, CYRUS, modeled aspects of the episodic memory of Cyrus Vance (when he was Secretary of State). CYRUS contained episodes described in the press, e.g. trips to foreign countries, summit meetings, treaty negotiations, etc. Unlike hierarchical Kohonen maps, which have a fixed-size per map and hierarchical depth, Kolodner's memories consisted of multi-indexed symbolic structures of arbitrary depth. However, Kohonen maps have the ability to encode finer regions within areas of the same map, and so can encode hierarchical structure.
Kolodner also modeled a complex set of heuristics for generating retrieval cues automatically -- i.e., to search memory in those cases in which indices did not exist directly. For example, CYRUS did not have an index of wives-meeting-wives, yet it could still recall times that Vance's wife met Menachim Begin's wife, by generating possible retrieval cues (e.g., trips to Israel in which wives are taken along and embassy parties). No such meta-level knowledge (i.e. of how memory is indexed) yet exists or is employed in connectionist models. However, this lack is probably more due to the youth of the connectionist NLP field, which only began to develop in the late 1980s. To my knowledge, Miikkulainen's model is the first to even attempt to model episodic memory. The advantage of the connectionist approach is that the resulting memory exhibits well-known connectionist features, namely, it is robust to noise/damage and provides parallel, associative retrieval from subsymbolic cues.
6. Role of Working Memory
In addition to lexical, semantic and episodic memories, there is a need for a limited capacity but rapid memory -- in which intermediate structures can be built and manipulated. For example, in Touretzky and Hinton's (1988) distributed connectionist production system (DCPS), a coarse-coded (Rumelhart and McClelland 1986) working memory is used to store sets of triples. Production rules are then "matched" (via spreading activation) to determine which rule to fire next. In Barnden's connectionist implementation of Johnson-Laird's model of syllogistic reasoning (Barnden 1991; in press; Barnden and Srinivas 1991; Johnson-Laird 1983) a central component is a connectionist working memory (termed Conpost) in which instances of predicates (representing objects, events, etc.) can be rapidly represented and bound to one another. The method, by which this rapid binding is performed, is unique. Barnden employs a unique approach to representing transient bindings, termed Relative-Position Encoding. Conpost's working memory consists of a 2-dimensional matrix where each cell in the matrix consists of a complex subnetwork capable of a number of operations. One of these operations is to notice configurations of activation patterns in neighboring cells. Such operations allow symbols (represented as activation patterns within a given cell) to be bound simply by being placed in any one of the 8 contiguous cells surrounding a given cell. This 8-cell region places an upper limit on the number of symbols that can be bound into a single structure, so Barnden employs an additional binding mechanism, termed Pattern Similarity Association. Namely, structures are bound to one another if they share the same symbols. Each cell of the matrix is quite complex and can perform numerous operations. Barnden argues that such complexity is needed to model human syllogistic reasoning.
Another situation requiring working memory is in the dynamic linking of recursive structures. For example, in efficiently parsing embedded relative clauses, Miikkulainen (this volume) employs a RAAM to act as stack, in order to push/pop clauses appropriately as they are parsed into case-role vectors.
7. Routing and Control
Both localist and multi-module distributed CNs require methods for controling the sequencing of operations and for routing information among different modules. Localist networks must control along what pathways signatures are to travel. For example, in the ROBIN system (Lange and Dyer 1989; Lange in press), there are nodes whose connections act to control or gate connections between other nodes. If ROBIN receives "John inhaled the pot" as input then activation will not spread at all to the FLOWER-POT meaning of "pot", because gating nodes will only let through signatures within a given set (i.e. in this case, different types of gases). Thus, gating acts to greatly reduce the amount of spreading activation that occurs and to impose syntactic and semantic restrictions on inference propagation.
In most distributed CNs, control processes are specified procedurally. For example, in DISCERN all routing of patterns between modules, and control of when modules execute (during both learning and performance), are specified by designer-specified procedures.
Miikkulainen (in press), however, has shown how control can be learned automatically. His SPEC model, designed to parse embedded relative clauses, contains 3 modules: (a) a SRN which takes as input an sentence with embedded clauses, (b) a RAAM (which acts a stack) and (c) a three-layer PDP network, termed the Segmenter. It is the job of the Segmenter to determine when to push or pop the stack, based on the current state of the parse (i.e., due to encountering clause boundaries for right branching vs. left branching vs center embedded clauses). Miikkulainen's work shows that distributed connectionist architectures can be trained to control their operations instead of having to employ a top-level, non-connectionist procedure.
With respect to all CNs, one can imagine a "granularity spectrum". At one end of the spectrum are purely localist CNs, with potentially many thousands/millions of nodes, each representing an individual type or instance. Here each single node acts as a module; the grain size is very small and the number of modules is extremely large. At the other extreme of the granularity spectrum lies, say, a single SRN, where each layer consists of an extremely wide vector. Here the granularity is very coarse, with only 1 module (consisting of 3 layers with one set of recurrent connections). The problems with the localist extreme are: (a) a combinatorial explosion of nodes are needed to represent world knowledge -- e.g., the problem of representing all possible visual angles and other information concerning one's grandmother via separate "grandmother neurons" (Feldman 1989), (b) the difficulty of incorporating learning, and (c) the recruitment of neurons/connections in forming long-term memories dynamically. The problems with the other extreme (i.e. single SRN) are: (a) learning to set the weights (especially when performing complex task involving language and higher-level reasoning) will take an impossibly long time, and (b) all brains exhibit a lot of specialization of circuitry and modularization (even if the modules are heavily overlapping). Miikkulainen and Dyer (1990) have shown that breaking up the the story paraphrase task into 4 modules (each independently trained yet communicating via a common lexicon) dramatically reduces the overall training time. This approach is an obvious -- i.e. one of divide and conquer. But the DISPAR and DISCERN modules still lie very much near the single module extreme of the spectrum, since they contain under a dozen, relative large modules. Can we imagine architectures with modules that are finer than those in DISCERN, perhaps hundreds or a few thousand, but far fewer than those at the localist extreme? This level of granularity would correspond more to how the brain appears to be organized.
The DCAIN system (Sumida 1991; Sumida and Dyer 1989, 1992) lies within this region of the spectrum. It is a distributed CN which consists of (potentially many hundreds of) ensembles of units. The global organization between ensembles is like that of a semantic network. Thus, these networks are termed Parallel Distributed Semantic (PDS) networks. Each ensemble is connected to other ensembles via multiple adaptive connections which are themselves under the control of learnable routing ensembles, termed propagation filters (Figure 3).
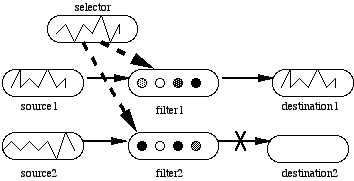
Figure 3. Propagation filter arrangement. A pattern (jagged lines) over the selector ensemble causes one filter ensemble to go above threshold and allows routing of a pattern from source1 to destination1 while blocking the propagation of other patterns. Arrows represent full connectivity.
A propagation filter consists of a selector ensemble of units and a filter ensemble. When a particular pattern of activation occurs over the selector ensemble, every unit in the filter group is driven above threshold, which allows an activation vector to be routed (over multiple connections) from a source ensemble to a given destination ensemble.
In DCAIN, each distinct type of semantic or syntactic information is represented as an ensemble of connectionist units. Each ensemble is connected to other ensembles based on semantic/syntactic relations between types. For example, the predicates BUYS and OWN and their roles would be represented each as a distinct ensemble. To represent the implication that [ x BUYS -y ===> x OWNS y], the roles of the BUYS ensemble are connected to the appropriate roles of the OWNS ensemble. Thus, at the ensemble level, PDS networks share organizational principles with localist networks. However, there are no separate instance nodes. Instead, each instance of a type (e.g. BUYS1 -- say, that John bought a TV from Sears) is represented as a particular pattern of activation that occurs within the BUYS ensemble. Thus, an exponential number of instances can be stored and the problem of node recruitment (at least for representing instances) does not arise. The relationship between a predicate ensemble and its role ensembles is similar to that of an autoassociative encoder network. That is, there are connections from role ensembles to the predicate ensemble and back and these connections are dynamically modified (during learning) so that the activation pattern over the predicate ensemble will cause the reconstruction of the correct role ensembles and vice versa. For example, if the pattern for BUYS1 is placed in the BUYS ensemble, then that pattern will cause the role ensembles to reconstruct (via pattern completion) the following values: BUYER = John and FROM = Sears. Thus, unlike localist CNs (which have relationships between role values and predicate instances specified by hand), PDS networks learn this relationship. Also, PDS networks can store more than one type within a given ensemble. For instance, BUYS could be a pattern of activation over an ensemble designated to be an ACT ensemble, while OWNS might be a pattern of activation over a more general STATE ensemble. Thus, the ACT ensemble might hold other actions (besides buying) and the STATE ensemble might hold other states (besides the OWN state). Syntactic categories (e.g. SUBJECT, DIRECT-OBJECT) are also represented as ensembles and a parsing analysis that, say, John is the subject of a sentence, is represented by propagating the John pattern of activation to the SUBJECT ensemble. Relationships among syntactic and semantic pieces of knowledge are represented in terms of propagation filters, which determine how patterns are propagated among ensembles. Figure 4 illustrates syntactic/semantic analysis of simple sentence, i.e. of the form [SUBJECT, VERB, D-OBJECT]).
Notice that, in Figure 4, the pattern for "boy" controls its own routing, i.e. causing it to be routed to the humans ensemble (vs. the animals ensemble). The pattern in the humans ensemble can only be routed to the subj ensemble after the correct kind of noun-phrase pattern has arrived in the NP ensemble. The correct pattern in the NP ensemble will cause patterns for "the" and "boy" to be reconstructed in the DET and N ensembles. The correct pattern in the Basic-S ensemble will cause its appropriate roles (in this case, subj = boy, verb = hit, dir-obj = dog) to be reconstructed in its role ensembles. When "the cat" is input, existing patterns over the NP and verb ensembles will cause "cat" to be routed to dir-obj (vs. to subj). This part of the analysis is not shown in the figure. Note that each predicate/roles encoder network and selector/filter group is trained to perform its reconstruction (or routing) task.
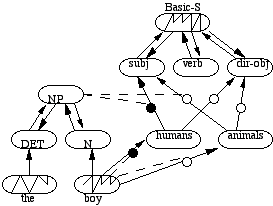
Figure 4. A fragment of a simplified PDS network showing some of the interaction between syntactic and semantic elements when parsing the phrase "the boy" from the sentence "The boy hit the cat". Propagation filters are small circles with black color indicating filters that allow allow patterns to be propagated. Two-way arrows between predicate and role ensembles (ovals) represent autoassociative encoder networks, with a predicate serving as a hidden layer and the roles serving as both input and output layers (i.e. the output layer is "folded" back onto the input layer). Dotted lines are from ensembles (that act as selectors) to filters.
The word "hit" has different interpretations, depending on context. For example, it can mean to perform music, as in "The boy hit the note." Figure 5 shows how filters propagate role bindings, based on the context within which "hit" appears.
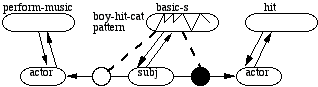
Figure 5. Pattern-based routing to perform word disambiguation. The pattern for boy-hit-cat appearing over the basic-s ensemble causes a filter to open and propagate the subject of the sentence to the actor role of the hit ensemble.
PDS networks retain many of the advantages of both localist and distributed CNs. Training PDS networks is more rapid than training distributed CN architectures with just one (or a few) modules because each PDS subnetwork is small and can be trained independently. In general, more modules of smaller size will result in faster overall training when implemented over a parallel architecture. Since there are many modules in separate locations, it is possible to pursue in parallel many distinct inference paths at the knowledge level. Novel instances can be created dynamically by forming new patterns over existing ensembles. Since role ensembles are connected to predicate (type) ensembles in the manner of encoder networks, they have the ability to perform pattern completion (i.e. roles reconstructing its predicate instance or a predicate instance reconstructing its roles) and to generalize to related patterns. As a result of pattern completion, PDS networks can propagate structured bindings -- i.e., a pattern laid over a type ensemble will cause the reconstruction of all of its role bindings in the associated role ensembles. These role patterns can then be routed to other predicate ensembles, thus causing their roles to be reconstructed, and so. If there is only one ensemble for a given predicate then only one instance (e.g. only TELL1 or TELL2, but not both) can be active at a time. However, it is possible to sequence through these instances over time (e.g. first filling the N ensemble with "boy" and then later with "cat" in The boy hit the cat"). This sequencing is controlled by propagation filters. Finally, because predicate/role ensemble groups are trained via example to act as encoder networks, they extract statistical regularities from the training data. Their distributed representations also allow them to exhibit robustness in the face of noise and/or damage because the loss of a unit within an ensemble will only degrade its performance, not destroy it. In addition, PDS networks reside in a region of the "granularity spectrum" that is closer to that of the brain (i.e. than either purely localist or distributed CNs with just a few modules).
8. Grounding Language in Perception
Although language relies on (and manipulates) highly abstract concepts and other forms of knowledge, it appears to be the case that children acquire early language semantics by associating verbal utterances (e.g. from adult care-givers) with ongoing sensory/motor experiences. Consider (one meaning of) the word "passing". After the child has learned simple objects by verbal/visual association (e.g. "ball", "car", "dog") the child can begin to learn the meaning of "passes" (e.g. as in "the car passes the dog") by simultaneously observing a car moving along, coming up from behind the running dog and then outstripping the dog, with both moving in the same direction. At the same time the child hears the phrase "car passes dog" (or, in the case of deaf children, receives a gestural sequence as visual input). By watching different size/shape/color objects catch up to and pass one another, the child can begin to form a perceptually based representation of the word "passes". It is unclear what a candidate symbolic representation would be. More likely, a major part of the meaning of "passes" consists of a generalized spatio-temporal visual experience. This perceptually based representation can then serve as a foundation for more abstract representations (such as "passes" later meaning that one becomes superior to someone else in a given cognitive skill, like playing chess, or that one "passes" an exam, etc.).
The task of mapping the abstract symbols of language to/from perceptual/motor experience has been called variously, the "symbol grounding task" (Harnad 1990), "L
0 language acquisition task" (Feldman et al. 1990) or "perceptually grounded language learning task" (Nenov 1991; Dyer and Nenov 1993). This task has been addressed by several connectionist researchers.Regier (1992) developed a connectionist network that learns the meanings of phrases by associating them with two simple objects (where one is a stationary landmark and the other is moving relative to it in a 2-D microworld). This research is part of the L
0 Project led by Feldman (Feldman et al., 1990) at the International Computer Science Institute at Berkeley, CA. The long-term goal of the L0 Project is to acquire language via association with perception. The architecture is designed to extract object features (e.g. center of mass and major axis orientation) and spatial features (e.g. concerning the relative angle, orientation, and distance of the moving object with respect to the landmark). These spatial features are extracted by non-neural, procedural modules. The resulting representations consist of both feature vectors and 2D feature maps. The feature maps are trained to produce, on the output layer, descriptions of the motion sequences. The learning method is a variant of backpropagation learning, in which every positive instance (during training) for a given spatial concept constitutes weak, implicit negative evidence for all other spatial relationships being learned. Regier argues that this modification allows the system to learn from positive examples only. He points out that in the child acquisition data, children acquire language apparently without the benefit of negative evidence (Pinker 1989). Regier's system consists of distinct and independent modules, each with a different connectivity arrangement and learning/activation parameters.The DETE system (Dyer and Nenov 1993; Nenov and Dyer in press-a, b, c) also learns the meanings of word sequences via association with simple moving objects. The DETE system's microworld (called Blobs World) consists of a simulated (64x64 "pixels") visual screen (VS) of up to five 2-D, homogeneous, mono-colored (and possibly noisy) "blobs" of various shapes (e.g. rectangular, circular, triangular). During learning, DETE receives also a simulated verbal sequence describing the visual sequence. Motor sequences may also be input, which tell DETE how to move and/or zoom in/out its single EYE. DETE also has a FINGER which can be made to touch or push blobs. After learning, DETE performs two tasks: (a) Verbal-to-visual/motor association -- given a verbal sequence, DETE generates the visual/motor sequence being described. (b) Visual/motor-to-verbal association -- given a visual/motor sequence, DETE generates a verbal description of it.
The current version of DETE is a massively parallel model that consists of over 1 million virtual processors, executing on a 16K processor CM-2 Connection Machine. Interface modules (i.e. that map simulated visual/verbal input to learning/memory subsystems) are parallel, array-processing (non-neural) procedures, while internal processing/memory modules themselves are modeled as highly structured neural networks modules (termed katamic memory) with each composed of novel neural elements.
Like a child, DETE must be taught incrementally. In a series of learning experiments DETE was first taught the names of blobs by being given scenes of blobs with a single shape, but with varying colors, sizes, locations and motions. As a result, DETE extracts what is invariant (i.e. shape) and forms the strongest associations between verbal input (e.g. "circle") and its internal representations for size, shape, etc. DETE next learned the meanings of words for color, size and location with respect to center of the VS (e.g. "above", "right", "in_center", "far", etc.). DETE then learned single words for actions/events. Such words include: "moves", "accelerates", "turns","bounces", and "shrinks" (i.e. change in blob size). Once these words were learned, DETE was tested by presenting it with verbal input only, and DETE indicates its comprehension by generating internal representations of this visual behavior. DETE's syntactic ability is currently limited to extracting word preference order (e.g. that size terms come before color terms) and the most complex sentences it has learned are of the sort: "big red ball moves diagonally down ... bounces ... moves diagonally up."
In DETE all visual/motor input is mapped (by non-neural interface routines) to regions of active neurons over a set of Feature Planes (FPs). The 5 visual FPs are: Shape (SFP), siZe (ZFP), Color (CFP), Location (LFP) and Motion (MFP). Each FP is composed of a 2-D array of 16 x 16 (256) neurons. Different active regions within a Feature Plane represent different values for that feature. An active neuron is one that oscillates, i.e. it fires periodically (with output 1) and is silent the rest of the time (with output 0). FPs have either a raster-linear or topographic layout. For instance, the LFP and MFP have topographic layouts. If a blob is in the lower right corner of the VS, then its position will be represented by a region of active neurons in the lower right corner of the LFP. On the MFP, the speed of a blob is represented by distance from the center, with stationary objects at the center and more rapidly moving objects toward the periphery. There are also FPs for FINGER and EYE dynamics. Figure 6 shows a (simplified) sequence of images on the VS, along with the visual representations that are produced (by array processing procedures) over a subset of the Feature Planes.
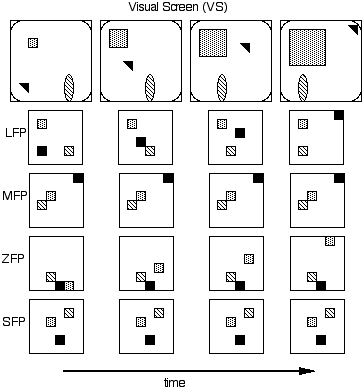
Figure 6. Visual Screen (VS) and Location (LFP), Motion (MFP), Size (ZFP) and Shape (SFP) Feature Planes (color, FINGER and EYE FPs are not shown here). Three blobs are moving on the VS. The oval blob is moving left; the square blob is growing and the triangular blob is moving diagonally upward toward the right. As blobs move/change on the VS, their active regions on the FPs are updated. Similar texture of active regions (small squares) indicates that these regions are firing in phase.
DETE makes use of phase locking to handle the "feature binding problem". For example, if both a big-region and small-region of the size FP are active and also both a square-region and circular-region of the shape FP, then how is DETE to distinguish whether what is being represented is: (a) a small circle and a large square or (b) a small square and large circle? DETE solves this feature-binding problem by breaking down its basic processing cycle into phases and assigning a distinct phase to each blob. Thus, if it is a small circle and large square that is on the VS, the active small-region and active circular-region will both be firing with the same phase. This phase difference is represented pictorially in Figure 6 as distinct textures (with active regions for the same blob containing the same texture across all FPs). Whenever DETE looks at a given blob with its EYE, it assigns to the EYE the same phase as that blob. This temporally based binding of attention makes sure that DETE only learns to associate verbal sequences with visual sequences of those blobs to which it is attending. The use of multiple objects requires DETE to address the issue of attention. In contrast, Regier's model only contains 1 moving object, so it does not need to face this feature binding problem.
Feature Planes (FPs) are used as representational constructs for three reasons: (1) Neuropsycho-logical and Neurophysiological Support: FPs correspond roughly to known neurophysiological and neuropsychological studies (Kandel 1985) indicating both topographic mappings and that shape, position, etc. are processed in different regions of the brain and then reintegrated. (2) Spatial Representational Analog: Topographic layouts supply simplified, yet direct analogs for spatial features, and thus make representing space and motion easier. For example, a word like "up" can be represented by activity anywhere in the upper area of the Location Feature Plane. A word like "moves" can be represented by activity anywhere away from the center of the MFP while directions of motion termed "diagonal" can be represented simply by activity anywhere in the diagonal regions of the MFP. FPs also support smooth generalization. If an object near the center of the MFP is moving slowly then objects mapped near to it will tend to be moving at about the same speed/direction. (3) Combinatorial Learning and Generalization Capability: Blob relationships and motions can be represented as a pattern of activity distributed over all FPs as they change sequentially in time. For example, the word "accelerate" can be represented and learned as a sequence of changing active regions, moving from the MFP's center toward its periphery. The use of separate/independent FPs also supports immediate generalization to novel combinations of known words. For instance, colors are mapped to one feature plane (i.e., CFP) while shapes are mapped to another (i.e. the SFP). As a result, once DETE has learned color terms and shapes (each separately), it can immediately understand novel combinations of these (e.g. "green ball", "green box", "red ball", etc.) -- i.e. by activating an appropriate region of each distinct Feature Plane.
Each pattern sequence (i.e., of multiple active, changing regions over a given 2-D Feature Plane) is fed as input to a corresponding Feature Memory (FM). Each FM consists of a katamic memory composted of a 2-D array of novel neural elements, termed predictrons and recognitrons. Predictrons learn to predict the next input and recognitrons sample their neighbors' outputs. For each cell of a given Feature Plane there is a corresponding predictron/recognitron within the associated Feature Memory. Each predictron contains a linear sequence of dendritic compartments (DCs) in which information is propagated, in a pipeline fashion, toward the body (soma) of the predictron. Thus, each predictron acts as a temporal delay line. This shifting property is somewhat analogous to that of Time-Delay Neural Networks (TDNNs) (Waibel 1989) . In addition, each predictron samples information spatially (i.e. from neighboring predictrons) and temporally (i.e. from earlier stages in the pipeline of DCs of other predictrons). Katamic memory has both novel processing and learning capabilities. Figure 7 shows a simplified picture of katamic memory.
Experiments on katamic memory, reported in (Nenov 1991; Nenov and Dyer in press-a, c), show that it has the following very useful properties: (1) Rapid learning: On average, only 4-6 exposures to a pattern sequence are sufficient for learning a novel sequence. This is 3-4 orders of magnitude improvement over recurrent PDP networks (Elman, 1990). (2) Flexible memory capacity: Multiple sequences of different lengths can be stored and the model is easily scalable to larger input patterns and/or sequences of greater length. (3) Sequence completion/recall: A short sequence (i.e. cue) is sufficient to discriminate and retrieve a previously recorded sequence. (4) Fault and noise tolerance: Missing bits can be tolerated and the memory can interpolate/extrapolate from existing data. (5) Integrated learning and performance: The katamic memory predictron can switch automatically from learning mode to performance mode. Thus, a katamic module can switch from learning to performance on a bit-by-bit and/or pattern-by-pattern basis. Also, whenever each predictron learns it uses positive evidence as a weak negative evidence for all other patterns. This allows DETE to learn, like Regier's model, from positive examples only.
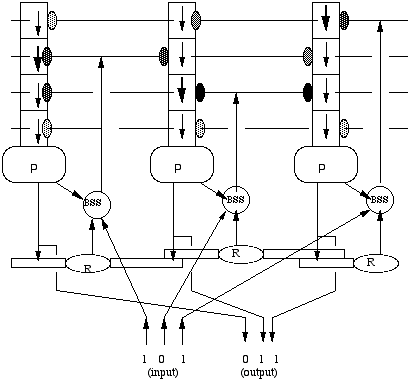
Figure 7. (Simplified) katamic memory, with only three predictrons (P), Recognitrons (R) and Bi-Stable Switches (BSS). Each BSS determines whether a predictron's Dendritic Compartments (DCs) get their input from the external environment or from internally generated outputs. Thus, BSSs are used for controlling when DETE attempts to perform sequence completion. Here, each predictron has only 4 DCs, illustrated as a train of squares above each predictron. Information about the input at a given region in a FP is shifted along the DCs in a pipeline fashion and is decayed over time (arrows of different thickness within each DC). Each recognitron here has two of its own dendritic compartments (RDCs), shown here as thin rectangles. These RDCs are used to sample the output of both its associated predictron and its neighbors (sampling of only one neighbor to-the-right shown here). Small vertical ovals indicate strength of input (via shading) to a predictron’s DC, arriving from neighboring predictrons predictions (via lateral lines). In DETE, a typical katamic memory module will contain 256 predictrons with 64 DCs per predictron.
9. Future Directions
The Regier and DETE systems are only first steps in grounding language learning in perceptual/motor experiences. Future directions in the area of representing perceptual experiences include: (a) extending the representations to 3-D objects, (b) representing composite objects with multiple motions -- e.g. a set of hinged blobs could represent a boy versus a dog, or the more complex actions of eating (e.g. by movements of the lips with a shrinking blob in front of them) and (c) representing abstract concepts. At this point, no matter how much DETE sees one blob, say, attached to another, it will not really be learning the abstract concept of OWNERSHIP (since it is just seeing physical attachment). Almost by definition, abstractions are never observed directly and appear to have some innate basis in human brains (otherwise animals could learn such concepts as RESPONSIBILTY simply by observing irresponsible actions). Thus there is a need to build connectionist systems that unite perceptually-based language learning with the existence of mental states, such as plans, goals, themes and emotions (Dyer 1983). At this point, only symbolic systems, e.g. (Dyer 1983; Wilensky 1983), are able to manipulate such constructs and in such systems these constructs are engineered by hand. The only distributed connectionist NLP system I am aware of that even attempts a goal/plan analysis of narrative text is the DYNASTY system (Lee 1991 ; Lee and Dyer in press). DYNASTY's goal/plan analysis capabilities are extremely limited and one critical component (i.e., working memory) are implemented via symbol manipulation.
In general, we need only look at recent symbolic NLP models to find a wide variety of systems that exhibit different and important aspects of high-level reasoning -- aspects not yet achieved by any connectionist model. For instance, the symbolic system OCCAM (Pazzani and Dyer 1989; Pazzani 1990) performs explanation-based learning (EBL) and thus can learn when given only a single example. EBL is not yet possible in connectionist models and Pazzani and Dyer (1987) have shown that backpropagation learning does concept formation in a way different than people (who have already built up some knowledge of the world). The symbolic story invention system MINSTREL (Turner 1992) not only creates new characters and events whose plot satisfies a theme, but it has both (a) analogical rules of invention, that map and adapt events from one domain to another, and (b) procedures that examine the appropriateness of a chain of events that have been created by a given heuristic rule. Within the connectionist paradigm, this chain-examination capability might be like having one network "examine" how well (or poorly) activation has spread along paths within another network. The symbolic system OpEd (Alvarado 1990; Alvarado et al. 1990a, b, c) reads a fragment of editorial text and constructs an "argument graph" of beliefs (concerning the efficacy of plans) that are linked by attack/support relationships. The argument graph is then traversed to answer questions.
Barnden (1992a, b) points out the need for connectionist NLP systems that can build explicit representations of rules, e.g. as when one is asked to read a rule of the sort: "Any town that's been declared a disaster area [...] gets federal aid." followed by "Rotville has been declared a disaster area." (Barnden 1992b, p. 29). Barnden's point is that we cannot rely on connectionist systems that just act as though they have rules (but without being able to access rules explicitly); otherwise we would not be able to build the rule and apply it, "on the fly", to conclude that Rotville will get disaster aid.
Another major direction for research is to understand how global CN structure might self organize -- e.g., either through evolution (Werner and Dyer 1991) or developmental self-organization (Kohonen 1988). Currently, the connectionist knowledge engineer must, ahead of time, specify all of the major modules and ensembles and specify their paths of intermodule connectivity. In the case of a single SRN there is little global structure to engineer. Unfortunately, SRNs have not been able to learn to perform the kinds of tasks achieved by CNs with multiple modules, such as DISCERN or DYNASTY. What the global structure of a connectionist network should be and how it might come about automatically is largely an open research issue.
10. Conclusions
What general morals can we take away with us, as the result of this overview? Here are a few: (a) There is no free lunch -- clearly, complex knowledge-level architectures are needed -- i.e., the mere existence of connectionist techniques is not going to eliminate the need for designing such architectures. General learning of complex cognitive tasks without preexisting network structure will always be intractable. Thus, some kind of "biasing" is required. NLP appears to be as complex as vision processing, so the structures needed may be as complex (or even more complex) as those in vision. (b) Time/space trade-offs will always exist -- e.g., we see this with the trade-off between many fine-grain modules and a few coarse-grain modules. In general, more modules allow more pieces of knowledge to be manipulated in parallel. Architectures with fewer modules are easier to train but take longer to do so and end up being more sequential at the knowledge level. (c) Limited cognitive processing is acceptable if it is psychologically plausible -- e.g. limits on the depth of a stack-like memory or on the number of identical predicates instances is reasonable if humans exhibit difficulty in processing similar texts. (d) Classical AI problems will remain for the foreseeable future -- e.g., humans are able to both construct and apply rules on the fly. (d) Solving the "perceptually grounded language learning" problem will not, by itself, give us sophisticated NLP connectionist systems -- abstractions must also somehow be encoded and/or acquired.
In spite of the difficulties facing connectionist NLP, it is still the case that great strides have been made. In the 1970s, NLP researchers built symbolic systems to read and answer questions about script-based stories. However, these systems were completely engineered. They did not learn any of their knowledge or processing skills. In the early 1990s, we see the arrival of, for instance, the DISCERN system -- that can read and answer (simple) queries concerning restricted (i.e. single script) stories (Miikkulainen 1993). However, it is important to realize that DISCERN acquires every piece of knowledge and every processing skill through learning -- specifically, learning by example. DISCERN learns the meaning of words; it learns to parse word sequences into vectors representing case-role information; it learns to generate completed script event sequences; it learns to encode scriptal (and semantic role) information in its modules' weights; it learns to generate word sequences that describe events; it learns to parse questions and generate appropriate retrievals and it forms episodic memories though a process of self-organization. The only things that are engineered in DISCERN are: (a) the global form of the modules, (b) how information is routed from module to module during learning/performance, (c) the learning algorithm itself and (d) the set up and presentation of the training data. It is clear that DISCERN represents quite an accomplishment and has provided us with major insights into novel forms of representation and processing.
At one extreme there are connectionist researchers who believe that connectionist models will sweep away all forms of symbol manipulation (Churchland 1986; Churchland and Sejnowski 1989). At the other extreme are symbolically oriented researchers who claim that connectionism will never be more than a "mere implementation" (Pinker and Mehler 1988) and "all of the action" is at the symbolic level. So far, the results are mixed. Connectionism has not advanced enough to offer alternative to the conveniences of symbol processing and thus attract away the majority of symbol pushers in traditional AI. If/when this happens, then connectionist processing will become preferred (since it offers a wide variety of nice features and potential links to brain research, etc.). However, existence of connectionist technologies and theories are not going to make knowledge representation, application of knowledge and reasoning issues magically disappear. Hopefully, connectionist technology and theory will continue developing and at some point the scales will tip in favor of connectionist implementations for all forms of high-level reasoning, but a need to understand processing at the knowledge/symbolic level will remain.
Acknowledgments
I would like to thank some of my past and current graduate students (S. Alvarado, C. Dolan, T. Lange, G. Lee, R. Miikkulainen, V. Nenov, M. Pazzani, R. Sumida, S. Turner, Y. Wang, and G. Werner) for their implementational and research contributions to NLP areas discussed here -- areas spanning from symbolically based story invention to neurally and perceptually based language learning.
References
Ajjanagadde, V. and Shastri, L. (1989). Efficient Inference with Multi-Place Predicates and Variables in a Connectionist System. Proceedings of the 11th Annual Conference of the Cognitive Science Society. LEA Press, Hillsdale NJ. pp.396-403.
Alvarado, S. J. (1990). Understanding Editorial Text Kluwer, Norwell, MA.
Alvarado, S., Dyer, M.G. and M. Flowers. (1990a). Argument Representation for Editorial Text. Knowledge-Based Systems. Vol. 3, No. 2, pp. 87-107.
Alvarado, S., Dyer, M.G. and M. Flowers. (1990b). Argument Comprehension and Retrieval for Editorial Text. Knowledge-Based Systems. Vol. 3, No. 3.
Alvarado, S. J., Dyer, M. G. and M. Flowers. (1990c). Natural Language Processing: Computer Comprehension of Editorial Text. In H. Adeli (Ed.). Knowledge Engineering, Vol. 1, Fundamentals. pp. 286-344, McGraw-Hill, NY.
Barnden, J. A. (1991). Encoding complex symbolic data structures with some unusual connectionist techniques. In: J. A. Barnden and J. B. Pollack (eds.), High-Level Connectionist Models. Ablex Publ., Norwood, NJ. pp. 180-240.
Barnden, J. A. (1992a). Connectionism, Generalization and Propositional Attitudes: A Catalogue of Challenging Issues. In J. Dinsmore (ed.), The Symbolic and Connectionist Paradigms: Closing the Gap. LEA Press, Hillsdale NJ. pp. 149-178.
Barnden, J. A. (1992b). Connectionism, Structure-Sensitivity, and Systematicity: Refining the Task Requirements. Memoranda in Computer and Cognitive Science, No. MCCS-92-227, Computing Research Lab., New Mexico State University, Las Cruces NM.
Barnden, J. A. (in press). Complex Symbol-Processing in a Transiently Localist Connectionist Architecture. In: R. Sun and L. Bookman (eds.). Computational Architectures for Integrating Neural and Symbolic Processes. ***
Barnden, J. and Srinivas, K. (1991). Encoding Techniques for Complex Information Structures in Connectionist Systems. Connection Science. 3(3)269-315.
Churchland, P. S. and T. J. Sejnowski. (1989). Neural Representation and Neural Computation. In L. Nadel, L. A. Cooper, P. Culicover and R. M. Harnish (eds.). Neural Connections, Mental Computation. Bradford Book, MIT Press, Cambridge MA.
Churchland, P. S. (1986). Neurophilosophy: Toward a Unified Science for Mind-Brain. MIT Press, Cambridge MA.
Dolan, C. P. (1989). Tensor manipulation networks: Connectionist and symbolic approaches to comprehension, learning, and planning. Ph.d. Dissertation, Computer Science Dept. UCLA, Los Angeles, CA. (To be published by LEA Press).
Dolan, C. P. and Smolensky, P. (1989). Tensor product production system: A modular architecture and representation. Connection Science. 1:53-68.
Dolan, C. P. and M. G. Dyer. (1989). Parallel Retrieval and Application of Conceptual Knowledge. In D. Touretzky, G. Hinton, T. Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summer School. Morgan Kaufmann, pp. 273-280.
Dyer, M.G. (1983). In-Depth Understanding. MIT Press, Cambridge, MA.
Dyer, M. G. Distributed Symbol Formation and Processing in Connectionist Networks. Journal of Experimental and Theoretical Artificial Intelligence, Vol. 2, 215-239, 1990.
Dyer, M.G., Cullingford, R. & Alvarado, S. (1987). Scripts. In: S. Shapiro (Ed.) Encyclopedia of Artificial Intelligence. John Wiley & Sons, pp. 980-994.
Dyer, M. G., Flowers, M. and Wang, Y. A. (1992). Distributed Symbol Discovery through Symbol Recirculation: Toward Natural Language Processing in Distributed Connectionist Networks. In: R. G. Reilly and N. E. Sharkey (eds.), Connectionist Approaches to Natural Language Processing, LEA Press, Hillsdale NJ, pp. 21-48.
Dyer, M. G. and Nenov, V. I. Language Learning via Perceptual/Motor Experiences. Proceedings of the Fifteenth Annual Conference of the Cognitive Science Society, LEA Press, Hillsdale NJ, 1993.
Elman, J. L. (1990). Finding structure in time. Cognitive Science, 14:179-211
Feldman, J. A. (1989). Neural Representation of Conceptual Knowledge. In: L. Nadel, L. A. Cooper, P. Culiver and R. M. Harnish (eds.). Neural Connections, Mental Computation. Bradford book/MIT PRess, Cambridge MA.
Feldman, J. A., Lakoff, G., Stolcke, A. and Hollbach Weber, S. (1990). Miniature Language Acquisition: A touchstone for cognitive science. Techn. Rep. TR-90-009, ICSI, Berkeley, CA.
Harnad, S. (1990). The Symbol Grounding Problem. Physica D, 42: 335-346.
Hinton, G. E., McClelland, J. L. and Rumelhart, D. E. (1986). Distributed Representation. In: D. E. Rumelhart and J. L. Mcclelland (eds.). Parallel Distributed processing, Vol. 1, MIT Press, Cambridge MA.
Johnson-Laird, P. N. (1983). Mental models: towards a cognitive science of language, inference and consciousness. Harvard University Press, Cambridge MA.
Kandel, E. R. (1985). Processing of Form and Movement in the Visual System. In E. R. Kandel and J. H. Schwartz (Eds.), Principles of Neuroscience (Second Edition), (pp. 366-383), Elsevier, NY.
Kohonen, T. Self-Organization and Associative Memory. Springer-Verlag (2nd ed.), 1988.
Kolodner, J. L. (1984). Retrieval and Organizational Strategies in Conceptual Memory: A Computer Model. LEA Press, Hillsdale NJ.
Lange, T. E. (in press) ********* In: R. Sun and L. Bookman (eds.). Computational Architectures for Integrating Neural and Symbolic Processes. ***.
Lange, T. E. and M. G. Dyer. (1989a). Frame Selection in a Connectionist Model of High-Level Inferencing. Proceedings of the Eleventh Annual Conference of the Cognitive Science Society (CogSci-89). LEA Press, Hillsdale NJ.
Lange, T. and M. G. Dyer. (1989b). Dynamic, Non-Local Role Bindings and Inferencing in a Localist Network for Natural Language Understanding. In D. S. Touretzky (Ed.). Advances in Neural Information Processing Systems 1. San Mateo, CA: Morgan Kauffman, pp. 545-552,.
Lange, T. E. and Dyer, M. G. (1989c). High-level inferencing in a connectionist network. Connection Science, 1, 181-217.
Lange, T. E., Vidal, J. J. and Dyer, M. G. (1991). Artificial Neural Oscillators for Inferencing. In A. V. Holden and V. I. Kryukov (eds.). Neurocomputers & Attention, Vol. I, Manchester University Press.
Lee, G.(1991). Distributed Semantic Representations for Goal/Plan Analysis of Narratives in a Connectionist Architecture. Ph.D. CS Dept. UCLA.
Lee, G. and Dyer, M. G. (in press). Goal/Plan Analysis via Distributed Semantic Representations in a Connectionist System. Applied Intelligence.
Lee, G., Flowers M. and M. G. Dyer. (1990). Learning Distributed Representations for Conceptual Knowledge and their Application to Script-Based Story Processing. Connection Science, Vol. 2, No. 4, pp. 313-345. [Also reprinted in: N. Sharkey (ed.), Connectionist Natural Language Processing: Readings from Connection Science. (Chapter 11, pp. 215-247), Kluwer Academic Publishers, Norwell, MA. 1992.]
Miikkulainen, R. and Dyer, M. G. (1991). Natural language processing with modular PDP networks and distributed lexicon. Cognitive Science, 15 (3), 343-399.
Miikkulainen, R. (1993). Subsymbolic Natural Language Processing: An Integrated Model of Scripts, Lexicon and Memory, Bradford/MIT Press, Cambridge MA.
Miikkulainen, R. (in press). Subsymbolic Parsing of Embedded Structures. In: R. Sun and L. Bookman (eds.). Computational Architectures for Integrating Neural and Symbolic Processes. ***.
Minsky, M. (1985). The Society of Mind. Simon and Schuster, NY.
Nenov, V. I. (1991). Perceptually Grounded Language Acquisition: A Neural/Procedural Hybrid Model. Ph.D. Dissertation and Technical Report UCLA-AI-91-07, Computer Science Departmentt, UCLA.
Nenov, V. I. and Dyer, M. G. (in press-a) Perceptually Grounded Language Learning: Part 1 -- A Neural Network Architecture for Robust Sequence Association. Connection Science,5 (2).
Nenov, V. I. and Dyer, M. G. (in press-b) Perceptually Grounded Language Learning: Part 2 -- DETE: A Neural/Procedural Model. Connection Science, 5 (3).
Nenov, V. I. and Dyer, M. G. (in press-c) Language Learning via Perceptual/Motor Association: A Massively Parallel Model. In: Hiroaki Kitano (ed.) Massively Parallel Artificial Intelligence. AAAI/MIT Press.
Pazzani, M. J. (1990). Creating a memory of causal relationships: An integration of empirical and explanation-based learning method, Lawrence Erlbaum Associates (LEA Press) Hillsdale, NJ, 1990.
Pazzani, M. J. and M. G. Dyer. (1989). Memory Organization and Explanation-Based Learning. International Journal of Expert Systems: Research & Applications. Vol. 2, No. 3., pp. 331-358.
Pazzani, M. and M.G. Dyer. (1987). A Comparison of Concept Identification in Human Learning and Network Learning with the Generalized Delta Rule. Proceedings of 10th Inaternational Joint Conference on Artificial Intelligence (IJCAI-87). Morgan Kaufmann Publ., Los Altos CA. pp. 147-150.
Pinker, S. (1989). Learnability and Cognition: The Acquisition of Argument Structure. MIT PRess, CAmbridge MA.
Pinker, S. and Mehler, J. Eds., (1988). Connections and Symbols. Bradford/MIT Press. Cambridge, MA.
Pollack, J. B. Recursive Auto-Associative Memory: Devising Compositional Distributed Representations. Proceedings of the Tenth Annual Conference of the Cognitive Science Society Lawrence Erlbaum. Hillsdale, NJ, 1988.
Pollack, J. B. Implications of Recursive Distributed Representations. In D. S. Touretzky (Ed.) Advances in Neural Information Processing 1, Morgan Kaufmann Publ. San Mateo, CA, pp. 527-536, 1989.
Pollack, J. B. (1990). Recursive Distributed Representations. Artificial Intelligence 46:77-105.
Regier, T. (1992). The Acquisition of Lexical Semantics for Spatial Terms: A Connectionist Model of Perceptual Categorization. Ph.D. Dissertation. University of California at Berkeley
Rumelhart, D. E. and McClelland, J. L., eds. (1986). Parallel Distributed Processing. Vol. 1. Bradford Books/MIT Press.
St. John, M. F. and McClelland, J. L. (1990). Learning and Applying Contextual Constraints in Sentence Comprehension. Artificial Intellgence. 46:217-257.
Schank, R. C. and Abelson, R. P. (1977). Scripts, Plans, Goals, and Understanding. Lawrence Erlbaum, Hillsdale, NJ.
Shastri, L. and Ajjanagadde, V. (1990). An Optimally Efficient Limited Inference System. Proceedings of Eighth National Conference on Artificial Intelligence. AAAI Press / MIT Press, Menlo Park, CA. pp. 563-570.
Shastri, L. and Ajjanagadde, V. (1993) From simple associations to systematic reasoning. A connectionist representation of rules, variables and dynamic bindings using temporal synchrony. Behavoral and Brain Sciences, 16, (3), 417--494.
Smolensky, P. (1990). Tensor Product Variable Binding and the REpresentation of Symbolic Structures in Connectionist Systems. Artificial Intelligence 46:159-216.
Stolcke, A. (1989). Unification as Constraint Satisfaction in Structured Connectionist Networks. Neural Computation, 1(4): 559-567.
Strong, G. W. and Whitehead, B. A. (1989). A solution to the tag-assignment problem for neural networks. Behavioral and Brain Sciences, 12, 381-433.
Sumida, R. A. and M. G. Dyer. (1989). Storing and Generalizing Multiple Instances while Maintaining Knowledge-Level Parallelism. Proceedings of Eleventh International Joint Conference on Artificial Intelligence (IJCAI-89). pp. 1426-1431, (Distributed by Morgan Kaufmann Publ.).
Sumida, R. A. (1991). Dynamic Inferencing in Parallel Distributed Semantic Networks. Proceedings of Thirteenth Annual Conference of the Cognitive Science Society. LEA Press, Hillsdale NJ. pp.913-917.
Sumida, R. A. and Dyer, M. G. (1992). Propagation Filters in PDS Networks for Sequencing and Ambiguity Resolution. In J.E. Moody, S.J. Hanson and R.P. Lippmann (eds.) Advances in Neural Information Processing Systems 4, Morgan Kaufmann Publ., San Mateo, CA, pp. 233-240.
Sun. (1989). A discrete neural network model for conceptual representation and reasoning. Proceedings of the Eleventh Annual Conference of the Cognitive Science Society. LEA Press, Hillsdale NJ.
Sun, R. (1992). On Variable Binding in Connectionist Networks, Connection Science, 4(2):93-124.
Sun, R. (1993). Integrating Rules and Connectionism for Robust Reasoning. John Wiley and Sons, NY.
Touretzky, D. S. and G. E. Hinton. (1988). A Distributed Connectionist Production System. Cognitive Science, 12(3), pp. 423-466.
Tulving, E. (1972). Episodic and Semantic Memory. In: E. Tulving and W. D. Donaldson (eds.), Organization of Memory. Academic Press, NY.
Turner, S R. (1992). MINSTREL: A Computer Model of Creativity and Storytelling. Ph.D. Dissertation, Computer Science Dept. UCLA (to be published by LEA Press).
von der Malsburg, C. (1981). The correlation theory of brain function. Internal Report 81-2. Dept. of Neurobiology, Max-Plank-institute for Biophysical Chemistry.
von der Malsburg, C. and Singer, W. (1988). Principles of cortical network organization. In: P. Rakic and W. Singer (eds.), Neurobiology of Neocortex. (pp. 69-99). John Wiley & Sons Ltd., London.
Waibel, A. (1989). Consonant recognition by modular construction of large phonemic time-delay neural networks. In D. S. Touretzky (Ed.), Advances in Neural Information Processing Systems I. (pp. 215-223). Morgan Kaufman, San Mateo, CA.
Werner, G. M. and M. G. Dyer. (1991). Evolution of Communication in Artificial Organisms. In: J. D. Farmer, C. Langton, S. Rasmussen and C. Taylor (Eds.). Artificial Life II, Addison-Wesley.
Wilensky, R. (1983). Planning and Understanding: A Computational Approach to Human Reasoning. Addison-Wesley, Reading, MA.