Distributed Symbol Discovery through Symbol Recirculation:
Toward Natural Language Processing
in Distributed Connectionist Networks
*Michael G. Dyer
Margot Flowers
Yih-Jih Alan Wang
3532 Boelter Hall
Computer Science Department
University of California
Los Angeles, CA 90024
ABSTRACT
The generalization and noise handling capabilities of distributed connectionist networks depend on similar patterns in the input layer reconstructing related patterns (related by some similarity metric) in the output layer, based on the energy landscape established in "weight space". In most distributed connectionist systems, only the weights are altered during learning. The representations of the training set, encoded in the input/output layers, are not modified. In this chapter we discuss a method for dynamically modifying such representations, by maintaining a separate, distributed connectionist network as a symbol memory, where each symbol is composed of a pattern of activation. Symbol representations start out as random patterns of activation. Over time they are "recirculated" through the symbolic tasks being demanded of them, and as a result, gradually form distributed representations that aid in the performance of these tasks. These distributed symbols enter into structured relations with other symbols, while exhibiting features of distributed representations, e.g. tolerance to noise and similarity-based generalization to novel cases. Here we discuss in detail a method of symbol recirculation based on using entire weight matrices, formed in one network, as patterns of activation in a larger network. In the case of natural language processing, the resulting symbol memory can serve as a store for lexical entries, symbols, and relations among symbols, and thus represent semantic information.
1. Introduction
The standard position in both AI and linguistics, that natural language processing (NLP) is highly symbolic in nature, has recently come under critical review, e.g. (Churchland and Sejnowski 1989), (Dreyfus and Dreyfus 1988), (Reeke and Edelman 1988), (Smolensky 1988). Researchers in the distributed connectionist systems (DCS) camp have built architectures in which language-related tasks are reformulated as mapping tasks that are fundamentally associative in nature. Examples are: mapping syntax to semantics (McClelland and Kawamoto 1986), present to past tense (Rumelhart and McClelland 1986a), translating language L1 to L2 (Allen 1986), and mapping orthography to morphemes (Sejnowski and Rosenberg 1987). What motivates these researchers are the useful features displayed by distributed connectionist networks, namely: (a) graceful degradation to noise and damage, (b) automatic learning and generalization to novel inputs, (c) massive parallelism, (d) self-organization and reconstructive memory, and (e) increased neural plausibility, including lesionability (Rumelhart and McClelland 1986), (Smolensky 1988).
The enthusiasms generated by initial successes in connectionism, e.g. (Rumelhart and McClelland 1986), have prompted a counterattack by symbolically oriented psychologists and linguists, e.g. (Pinker and Prince 1988) (Fodor and Pylyshyn 1988), who have pointed out a number of fundamental weaknesses in language-related DCS models. Other researchers have responded by attempting to construct distributed connectionist architectures and hybrid symbolic-connectionist systems capable of various degrees of symbol processing, e.g. (Dolan 1989), (Dolan and Smolensky 1989), (Dyer in press), (Gasser 1988) (Gasser and Dyer 1988), (Hendler 1987, 1989), (Lange and Dyer 1989a, 1989b), (Pollack 1988), (Shastri 1988), (Smolensky in press), (Sumida and Dyer 1989), (Touretzky and Hinton 1988).
In this chapter, we take the position that NLP requires symbol processing (Dyer in press), (Touretzky 1989). Thus, if distributed connectionist systems are to handle natural language input with full generality, they must be able to exhibit the capabilities of symbol processing systems, namely: (a) representation of abstract and recursive structure, (b) implementation of rules and schemas, (c) inference chaining through propagation of bindings, and (d) formation of new instances and episodes in long-term memory.
The rest of this chapter is organized as follows: First, we discuss requirements for NLP, pointing out the symbolic nature of natural language comprehension through the use of an example involving abstract knowledge. Second, we examine in detail one method for dynamically forming distributed symbol representations. This method uses the technique of manipulating entire weight matrices in one network as a pattern of activation in another network, storing these distributed representations in a symbol memory, and then recirculating them as the system is required to relate symbols to each other in specified ways. As a result of this symbol recirculation, symbol representations are dynamically altered and converge on representations that aid in those tasks demanded of them. Third, we briefly review related methods of symbol recirculation. Finally, we discuss open problems in distributed connectionist symbol processing for natural language tasks and conclude with a brief description of some current approaches toward resolving these problems.
2. Natural Language Processing: Constraints from the Task Domain
Natural language processing systems must manipulate very abstract forms of knowledge, e.g. the goals, plans and beliefs of narrative agents. Consider just a fragment of the abstract knowledge needed to understand, and answer questions about, the following narrative segment:
Irresponsible Babysitter
John promised to watch the baby for Mary. John decided to talk to a friend on the phone. The baby crawled outside and fell into the swimming pool and nearly drowned.
Q: Why did Mary accuse John of being irresponsible?
A: John had agreed to protect the baby from harm, but the baby nearly drowned.
A portion of the necessary background knowledge needed to understand "Irresponsible Babysitter" includes abstract structures of the following sort (informally stated below):
<x "promise" y that z> =
<x communicated to y that x has goal G, satisfied by z>
<y communicated to x that y has goal G', to be agent for x>
<after communications, y believes that G(x), x believes that G'(y)
and y believes that x will execute action A to achieve G>
<x "watch" y "for" z> =
<x attends eyes(x) to y and
if possible act A of y can cause harm to y,
then x performs act B to block A>
<x can know act A of y by attending eyes of x to y at the time of A>
<possibility of drowning(x) threatens preservation health goal G(x)>
<if x loves y, then x has goal to block failure of health goal G(y)>
<"irresponsible" x (wrt y)> = <promise by x to achieve G(y)
followed by goal failure for y>
In addition we need to know facts such as:
<babies cannot swim and may drown in water>
<mothers love their babies>
The traditional approach to the NLP comprehension problem is to handcode such abstract symbolic structures in a semantic network of labelled relationships; then instantiate instances of such structures and bind them into larger structures in episodic memory. Once episodic memory is built, questions can be mapped into conceptual representations that direct retrieval strategies.
The mapping from natural language to conceptual representations is usually accomplished via instantiation and binding operations over symbol structures, performed by a conceptual parser, e.g. (Dyer 1983). Basically, as the parser encounters each word and/or phrase in the input (e.g. a sentence of a story or question about the story), it accesses a corresponding entry in lexical memory. Each lexical entry refers to one or more fragments of associated symbol structures (schemas) in a general semantic memory. These fragments are either explicitly connected to other schemas, via labelled links, or implicitly connected via rules. Examples of (informal) rules are:
if x communicates message m to y
then y knows m
if x cannot perform an act z
then x may ask y to perform z for x
if x loves y and x believes that y might perform an act z to cause harm to y,
then x will do an act r to keep y from doing z
Such rules are needed in order to interpret phrases such as "watch the baby", which are actually ambiguous. For example, in "Irresponsible Babysitter", John could conceivably argue that he was not irresponsible:
"I am not irresponsible. I agreed to watch the baby and I did. I watched the baby crawl out of the crib. I watched him crawl to the pool, and I watched him fall in. You wanted me to watch the baby and that is exactly what I did."
To interpret "watch" correctly, we need many inferences. We need to infer from John's promise to Mary that Mary believes that John will do what he promised; otherwise, we could accuse Mary of being irresponsible. We need to know that unattended babies may perform actions that will cause them harm (e.g. "watching a television" does not involve keeping the television set from harming itself). We also need to know that guardians often observe incompetent individuals to prevent them from coming to harm, so we need rules such as:
if x is a baby
then x may do an act that causes harm to x
if x is attending eyes to y and y typically performs acts that can cause harm
then x is probably attending eyes in order to be aware of such acts,
in order to block them
Given such rules, a conceptual parser must link conceptual representations for "promise", "watch" and "baby" into a coherent set of interrelated instantiations. Before this task can be performed by a distributed connectionist system, we must solve the problems of: (a) representing the above, abstract schemas, (b) representing the above rules, along with their variable portions, (c) propagating dynamic bindings along the variable portions, and (d) creating long-term episodes in memory.
Notice that these operations, while traditionally performed by symbol processing systems, need not necessarily be implemented as in von Neumann architectures. Symbols and symbol manipulations could conceivably be implemented via associative operations over distributed patterns of activation. However, no matter how they are implemented, capabilities of structure, inference, and instantiation must be realized (Feldman 1989). Notice also that the existence of symbols in distributed connectionist systems does not imply the denial of non-symbolic forms of knowledge. For instance, visual images (e.g. of John talking on the phone while the baby crawls off) could very well be non-symbol in nature. But without the capabilities to form and manipulate abstract structures (e.g. irresponsibility), it will be impossible to represent, infer, acquire or interpret instances of such abstract situations.
Once we accept the necessity for entitites that behave as symbols, major issues of research in designing distributed connectionist systems for high-level cognition become: How are distributed symbols automatically formed? How do such distributed symbols enter into structured relationships with other symbols?
3. Dynamic vs Static Symbol Representations
The purely symbolic approach to NLP can exhibit impressive performance on short segments of text within constrained domains of knowledge, e.g. narrative understanding and question answering (Dyer 1983, 1989), (Dyer et al. 1987), argument comprehension in editorials (Alvarado et al. 1986, in press), irony recognition (Dyer et al. in press), advice giving (Quilici et al. 1988) and moral evaluation of text (Reeves 1988). But the resulting complexity of knowledge interactions, the difficulty of engineering the knowledge by hand, and the fragility of the resulting systems is well known. Connectionists hope to overcome these problems through automatic learning of distributed structures. One positive consequence of the connectionist approach is the resulting reexamination of the nature of symbols and symbolic operations.
How should symbols be implemented? In von Neumann machines, symbols are implemented as bit patterns residing in separate memory registers. The bit patterns are specified by a predetermined coding scheme, such as ASCII. The encoding scheme is both arbitrary and static; e.g., the ASCII code for "CAT" remains the same throughout all system executions. In purely symbolic systems, the arbitrary and static nature of symbol representations are not viewed as any problem, since it is assumed that the semantics of a given symbol develops only in terms of the structured relationships it enters into with other symbols. While it is the case that symbols enter into structured relationships with other symbols, the arbitrary and static nature of von Neumann symbol representations results in the inability of standard symbolic models to perform associative inference, handle noise and damage, complete partial patterns, or generalize to novel cases.
In contrast, distributed connectionist systems can represent symbols as patterns of activation over a set of processing units in the input/output layers of a given network. These patterns of activation are intimately involved in the success (or failure) of the associative operations that are demanded of them. The generalization and noise handling capabilities of distributed connectionist networks depend on similar patterns in the input layer reconstructing related patterns (related by some similarity metric) in the output layer, based on the energy landscape established in "weight space".
In the prototypic case, a mapping task is established via a set of input/output pairs. During the training phase, a subset of these I/O pairs is presented to the network and the connection weights are adjusted incrementally, using some adaptive learning algorithm, such as back-error propagation (Rumelhart and McClelland 1986) or reinforcement learning (Sutton 1984). Once the network has been trained, the reserved subset of I/O pairs is used to test the generalization capabilities of the network. From an architectural point of view, the particular weight-update rule is not centrally important, just as long as the update rule is capable of finding a set of weights that realize the desired associations.
In most distributed connectionist systems, only the weights are altered during learning. The representations of the training set, encoded in the input/output layers, are not modified. In the cases where the input is language related, the input/output representations are usually encoded by hand, using some sort of microfeature scheme. For instance, McClelland and Kawamoto (1986) trained a network to associate a representation of syntactic input with semantic output. Both the input and output layers were divided up into segments (e.g., subject, object, prepositional phrase, etc. in the syntax layer; actor, action, instrument, etc. in the semantics layer), where a pattern of activation (PoA) over each segment represented a symbol. For instance, the symbol "John" might be represented by activating those units representing the microfeatures: animate, human, male, etc. The reason the network could generalize to novel mappings relied greatly on the similarity between symbols. Suppose the network learns the following mappings:
syntax layer semantics layer
SUBJECT: John ACTION: ingest
VERB: eats ---> ACTOR: John
OBJECT: hamburger OBJECT: hamburger
PREP-PH: with a fork INSTRUMENT: fork
OBJ-MODIFIER: xx
SUBJECT: Fred ACTION: ingest
VERB: eats ---> ACTOR: Fred
OBJECT: hamburger OBJECT: hamburger
PREP-PH: with cheese INSTRUMENT: xx
OBJ-MODIFIER: cheese
If the network is given the novel input:
SUBJECT: Mary
VERB: eats
OBJECT: hotdog
PREP-PH: with ketchup
then the extent to which it arrives at the correct interpretation of "with ketchup" (i.e. as either the modifier of the OBJECT versus the INSTRUMENT of the ACT) will depend on how closely "Mary", "hotdog" and "ketchup" share microfeatures with previous inputs. Clearly, if their patterns of activation do not share microfeatures, then the network will fail to generalize properly.
Unfortunately, microfeature encodings suffer from four major problems: (1) Knowledge engineering bottleneck -- the initial set of microfeatures must be determined. As is well known by AI researchers, the selection of a primitive set of features is itself a difficult knowledge engineering problem. (2) Flatness -- microfeature vectors are impoverished as a representation scheme since they are flat; i.e. they lack the ability to represent recursive and constituent structure. Such structures are necessary to capture embedded grammatical and conceptual regularities, as in "John told Mary that Bill thought Mary wanted to be kissed". (3) Inapplicability -- Many microfeatures will be inapplicable when representing various entities. For example, the microfeature say, METAL = {aluminum, copper, etc.}, will not be applicable for representing people. This results in requiring a huge number of microfeatures specified ahead of time, with most of them specified as negative or not-applicable. It seems counterintuitive to represent, e.g. a person or a building, in terms of the very large number of features that they lack. (4) Tokens vs Types -- It is awkward to distinguish a specific instance from a general concept using the microfeature approach. For example, the representations for a car, John's car, a convertible, a broken car, and an antique car must all be differentiated in terms of microfeatures. In the case of "John's car", it might seem sufficient to have some "ownership" microfeatures, but what do such microfeatures look like? Must we establish an ownership microfeature for each of the possible owners, so that "my car" and "John's car" can be distinguished?
4. Symbol Recirculation
What we want is a method by which symbols can enter into structured, recursive relationships with one another, but without microfeatures; while at the same time forming distributed patterns of activation. The general technique for accomplishing this goal we refer to as symbol recirculation. Symbols are maintained in a separate connectionist network that acts as a global symbol memory, where each symbol is composed of a pattern of activation. Symbol representations start out as random patterns of activation. Over time they are "recirculated" through the symbolic tasks being demanded of them, and as a result, gradually form distributed representations that aid in the performance of these tasks. Symbol representations arise as a result of teaching the system to form associative mappings among symbols, where these mappings capture structured relationships.
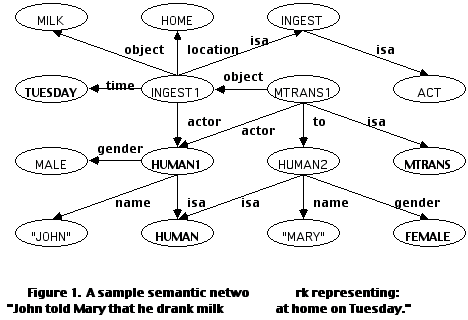
For instance, in NLP tasks, structured relationships among symbols can be represented as triples of the form (PREDICATE SLOT FILLER). For instance, "John told Mary that he drank the milk at home on Tuesday" can be represented as:
(MTRANS1 ACTOR HUMAN1)
(MTRANS1 TO HUMAN2)
(MTRANS1 OBJECT INGEST1)
(MTRANS1 ISA MTRANS)
(INGEST1 ACTOR HUMAN1)
(INGEST1 OBJECT MILK)
(INGEST1 TIME TUESDAY)
(INGEST1 LOCATION HOME)
(INGEST1 ISA INGEST)
(HUMAN1 ISA HUMAN)
(HUMAN1 NAME "JOHN")
(HUMAN1 GENDER MALE)
(HUMAN2 ISA HUMAN)
(HUMAN2 NAME "MARY")
(HUMAN2 GENDER FEMALE)
(INGEST ISA ACT)
...
Structured relationships among symbols can also be interpreted as a semantic network (Figure 1), where each SLOT is the name of a relation that links together two nodes (i.e.PREDICATE and FILLER).

In a distributed connectionist architecture, each symbol is represented as a pattern of activation over a set of processing units in the input layer of a distributed connectionist network.
The basic technique of symbol recirculation involves: (1) starting with an arbitrary representation for each symbol, (2) loading these symbols into the input/output layers of a network performing a mapping task, (3) forming a distributed symbol representation that aids in the mapping task, (4) storing the modified symbol representations back in the global symbol memory, and (5) iterating over all symbols for all mapping tasks, until all symbol representations converge. As the same I/O pairs are presented to the mapping network, the representations of the symbols making up these pairs undergo modification. As a result, the system is "shooting at a moving target", since the representations (of the mappings that the network must learn) are being altered while the network is attempting to learn the mapping. So not only are weights being modified, but also the encodings of the representations that are being associated. Thus, the training environment is reactive.
The approach we will describe in detail in this chapter is based on the following observation:
Any distributed connectionist network whose long-term memory is representable as a weight matrix (WMx), can be transformed into a pattern of activation (PoA) in the input layer of a larger network. Likewise, the PoA output by one network can be used to dynamically construct another network (WMx).
This fundamental relationship can be exploited in many ways. We describe one such method below.
5. Encoding Semantic Networks in DUAL: A Distributed Connectionist Architecture
DUAL is an architecture designed to form distributed representations of symbols that are related in the form of a semantic network. For our purposes here, a semantic network is a directed graph of nodes {...A
i...} and named links {... ri...}. It can be represented pictorially (Figure 2a) or as a case frame (Figure 2b). This sample semantic network (SSN) has four nodes: A1, A2, A3, A4, and three distinct links: r1, r2, r3.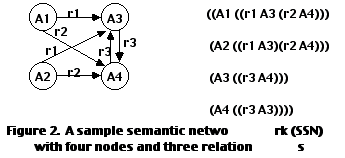
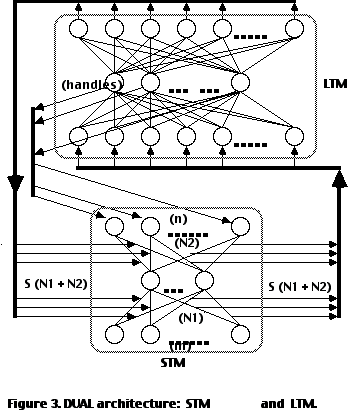
The essence of our approach (Dyer, Flowers, Wang 1988) is to maintain two distributed connectionist networks, STM and LTM (each with its own input, output, and hidden layers). STM acts as a short-term memory and encodes link-node pairs associated with a given node (symbol) in the semantic network (SN). LTM acts as a long-term memory and encodes an entire semantic network. STM and LTM are illustrated in Figure 3.
STM contains m input and n output units, connected by N1 weights to the hidden units and N2 weights to the output units. An entire matrix S of the STM contains N = N1 + N2 weights. LTM consists of N input units. Thus, the complete weight matrix (WMx) of STM is the input to LTM, as a pattern of activation (PoA). LTM acts as an autoassociator, with n hidden units. A pattern of activation over the hidden units in LTM, which we term a handle, can be used to retrieve a weight matrix S from LTM. Thus, LTM functions to compress an S into a handle and to store a number of S's into a single, long-term memory weight matrix.
In addition to STM and LTM, DUAL contains a Distributed Symbol Memory (DSM), where handles are stored. Each handle actually represents a symbol in the semantic memory, which indirectly encodes all of the link-node relationships associated with it. Over time, the representation of each handle changes, converging on a final representation for each symbol.
At any given point in time, STM holds all (rj Aj) link-node pairs associated with a given semantic network node Ai; DSM holds handles (symbols) that retrieve, from LTM, nodes A1...Ap (assuming p nodes in the semantic network); LTM holds the entire semantic network as a set of autoassociated, STM weight matrices.
Each link rj in DUAL is represented as an arbitrary, handcoded PoA over the input units in STM. In the current version of DUAL, the activity patterns for the links remain unchanged during encoding; only node representations are dynamically formed. A set of orthogonal representations is used for the links, in order to minimize interferences, since we want to keep links discriminated. For example, the three links r1, r2, r3 of SNN may be represented by the PoAs illustrated in Figure 4a.
Each node A
i is represented by its handle and the PoA of its handle is randomly set up initially and varies dynamically as the semantic network is encoded. The encoding process involves iterating over all nodes until a consistent set of handles have emerged.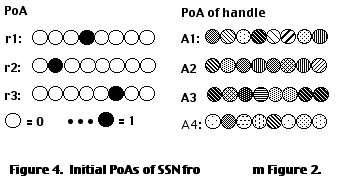
In the process of encoding, DUAL discovers distributed representations for the nodes of the semantic network, representations consistent with the desired operations over the semantic network. Figure 4b illustrates a possible set of initial PoAs of the handles for the nodes of SSN.
5.1. Encoding Semantic Memory Nodes in STM
A given node A
i in a semantic network is defined by the link-node pairs (rj Ak) that are associated with it. To encode Ai we perform the operation ENCODE-NODE(Ai):ENCODE-NODE(A
For example, in SNN (Figure 2), the node A
1 has two relationships (r1 A3) and (r2 A4). Therefore, ENCODE-NODE (A1) involves training the STM with two sets of input-output patterns: [PoA(r1) --> PoA(handle(A3))] and [PoA(r2) --> PoA(handle(A4))]. After training STM on these two patterns, the weight matrix in STM is designated as S1 (Figure 5).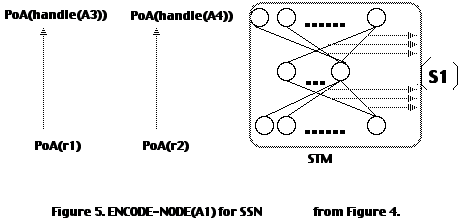
5.2. Encoding STM Weight Matrices in LTM
To encode a set of STM weight matrices {S
1...Sp} in LTM, we perform the operation LOAD-LTM:LOAD-LTM -- Train LTM with the set of {... S
Figure 6 illustrates the encoding of each S
i through autoassociation and the updating of handles in the Distributed Symbol Memory for each symbol/node/handle.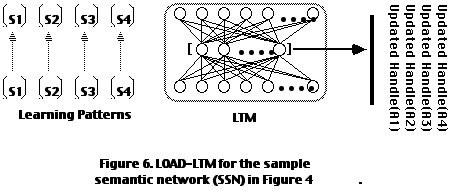
5.3. Recirculation to Convergence
At this point, each handle H
i, if placed in the hidden layer of LTM, will cause the corresponding Si to be reconstructed on the output layer of LTM . The resulting Si is then loaded into STM, through modification of the weights of STM. Figure 7 illustrates the operation of LS-TRANSF(H1), which consists of both loading handle H1 (of semantic node A1) into LTM and loading the resulting S1 into STM.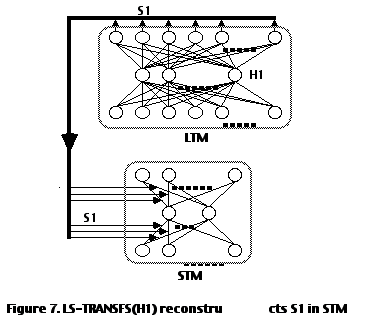
Now, suppose STM has S
i as it weight matrix. If we want to retrieve any relationship, say (rj Ak) associated with Ai, we simply place link rj on the STM input layer and a handle for Ak will appear on the output layer. Notice, however, that this handle is obsolete! That is, DSM contains a more current version Hk of Ak. Since we do not want Ai's link, rj, pointing to an obsolete version of Ak, we need to retrain STM with the new pair (rj Ak), where Ak = Hk.Consider a concrete example, where we focus on just two nodes (below) in a hypothetical semantic network:
node associated link-node pairs
JOHN (LIKES MARY), (GENDER HUMAN), (OWNS FIDO)...
MARY (LIKES JOHN), (GENDER FEMALE), (OCCUPATION STUDENT)...
To encode JOHN in STM we must encode the associations [LIKES --> MARY, ...]; but what is the teaching pattern we are going to use for the output layer of STM? Since we have not yet encoded MARY, we must select a random pattern, say P1. So we have really encoded JOHN LIKES P1, where P1 is a poor initial representation for the MARY symbol. Likewise, the pattern for JOHN (when encoding that MARY LIKES JOHN) must also be a random pattern, say P2. But once both JOHN and MARY have been encoded in LTM (via LOAD-LTM) and updated in DSM, then both JOHN and MARY now have patterns that are no longer as random, but which aid in reconstructing the respective weight matrices in STM that will allow their associated link-node pairs to be retrieved. So now we must again execute LS-TRANSF and ENCODE-NODE for both JOHN and MARY, followed again by LOAD-LTM. But this encoding operation will cause yet a new set of handles to be created for JOHN and MARY.
Each time JOHN LIKES MARY, JOHN is learning to LIKE a new representation of MARY. This associative learning operation is changing the weight matrix in STM that represents JOHN. As a result, the representation of JOHN is now different, which means that MARY must learn to LIKE this new representation of JOHN, which causes the representation for MARY again to be altered. So the process of ENCODE-NODE and LOAD-LTM (along with updating DSM) must recirculate, until the representations in DSM cease changing. At this point, convergence is achieved. After convergence, each semantic node A
i has a distributed representation Hi that encodes all of its structural information where the distributed representation is central in retrieving the weight matrix that makes this structural information available.
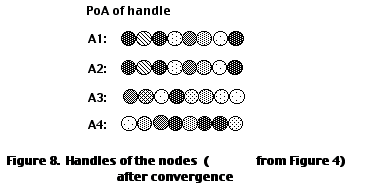
To summarize: In the encoding cycle we start the training of STM with one set of handles (node representations) and end up with a new set of handles in LTM. Therefore, the information we have encoded in the STM matrices (about the old handles) no longer holds for the new handles. However, updating old handles with new ones will require yet another encoding cycle to be performed. Thus, to encode the entire semantic network, DUAL must successively perform this encoding cycle repeatedly, until convergence of handles is achieved. This approach is analogous to "shooting at a moving target", where the act of shooting causes the target to move. As one "shoots", the target location has moved, so the aim has to be repeatedly adjusted. After convergence, we end up with only one set of consistent handles representing the semantic network nodes. Figure 8 illustrates a sample set of handles for SSN after convergence.
5.4. Retrieval and Accuracy/Capacity in DUAL
To retrieve the value of r
i for node Ai (with handle Hi), we do the operation GET(Ai, ri):GET(A
By repeatedly using GET(node, link), we can traverse the entire semantic network. However, due to the nature of distributed connectionist networks, a certain degree of inaccuracy is likely to be introduced as each S
i is encoded into LTM.To test both for change in accuracy of retrieval during recirculation, and to gain a rough estimate of time to convergence, a semantic network SNET was created, with 10 nodes and an average number of relations per node being 5. Each node of SNET was represented in the Distributed Symbol Memory (DSM) as a handle 8 bits long. Execution time was measured in terms of CPU seconds as epochs of symbol recirculation were run (Table 1). Here, a single epoch consists of (a) setting the weights in STM (via back-error propagation) for a given node, (b) iterating over all nodes in SNET, and (c) storing/compressing all S
i in LTM. The representations of the handles {...Hi...}, and thus also the weight matrices {... Si...}, will get updated from one epoch to the next.The retrieval error was calculated at the end of each epoch by collecting the VALUE's from the DUAL network for all the (PREDICATE REL VALUE) triples in SNET and comparing them with the the current handle representation for that VALUE in DSM. For example, to calculate the accuracy of retrieving the triple (A --> r --> C) during symbol recirculation, we first load the STM with the current weight matrix of A (i.e. S
A). Then we input pattern r to STM and collect the output as C'. We then compute the difference between C' and the current handle of C (i.e. H(C) in DSM) and divide by H(C). This is the measure of error. We do this operation for all triples and calculate the average to get the average error over all triples for that epoch.
Epochs Avg. Error CPU time (sec)
---------- --------------- --------------------
0 84.2% 1.2
2 28.5% 943
4 21.3% 1886
6 13.7% 2830
8 12.6% 3773
10 11.6% 4717
Table 1. Sample DUAL experiment on semantic network SNET;
CPU time calculated on a Hewlitt-Packard workstation (model HP 9000/320, ~ 1.7 MIPs).
The average error roughly indicates the degree of convergence. The lower the error, the more consistency exists in the representation set in DSM and thus the closer to convergence is the set of handles (distributed representations of nodes in SNET). In Table 1, the error drops as the set of handles converges.
5.5. Nature of Discovered Representations
In a von Neumann architecture, a unique address can be assigned initially to each node; whereupon the pointer fields for each link can be trivially specified. In DUAL, however, the representations for each node A
i are constantly changing as the representations of the nodes in each link-node pair (associated with Ai) undergo changes. This process occurs because each link must supply a handle for retrieving an entire weight matrix. In DUAL, each handle reconstructs its own, virtual distributed connectionist network, encoded within another, larger network.DUAL is able to encode the structural relations of a semantic network while at the same time dynamically forming distributed representations for each node, from an initially random set of patterns; as a result, microfeature-based representations are not needed. DUAL solves the microfeature representation problems of flatness, inapplicability, and tokens vs types by using patterns of activation to represent links that function as normal property names in AI systems. In a semantic network, the node pointed to by a link is interpreted as the value of that property. Only relevant properties (and their values) are associated with a given node. While only a small number of the relevant properties need be used per node, the potential number of different properties representable in a pattern of activation (PoA) can be very large. By using PoAs also to represent nodes, we solve the type-token problem, since a given PoA can represent a unique person, event, plan instance, object, etc. We also solve the problems of constituent and recursive structures since a semantic network with labelled links can represent such structures directly.
Experiments show that DUAL discovers distributed representations of the semantic nodes input to the system and that these representations are formed to facilitate the demanded retrieval tasks. Furthermore, DUAL automatically forms representations that reflect the similarity of nodes, with respect to the similarity of their structural relationships.
Similar semantic nodes are those with similar link-node associations. Before convergence, similar nodes may be represented by very different handles, although they are computing similar link-node associations. After convergence, however, similar nodes contain similar representations. For example, nodes A
1 and A2 in SNN are similar nodes (Figure 2). Their initial handles are distinct (Figure 4b). After convergence, their representations are identical (Figure 8). In general, representations become similar to the extent that they share similar link-node pairs.In addition, similar distributed representations among similar semantic nodes results in some statistical generalization to novel cases. That is, if A
i and Aj are nearly identical, except that Ai has link rk and Aj does not, then one can perform GET(Aj, rk) for a node Aj without relation rk, and have a likelihood of retrieving the value of GET(Ai, rk).
Consider two similar nodes A and B that share all identical relations, except that A has one more relation, say, (A->r->C). How will DUAL behave if we attempt to traverse link r from node B? This experiment was performed, for nodes having from 2 to 8 nodes in common (see Table 2). Here, the normal case retrieval error is calculated by the relative difference between H(C) and the output C' we get by actually loading the STM with SA and setting the input in STM to r. The generalization error is calculated in the same way for SB. The actual formula for measuring these two columns of error is similar to the one used for Table 1.
No. of Relations Normal Case: Generalization:
in common for error in traversing error in traversing
A and B r from A r from B
------------------ -------------------- ---------------------
2 0.20% 13.5%
4 0.87% 5.50%
6 0.99% 4.85%
8 0.68% 3.37%
Table 2. Generalization experiment
As demonstrated in Table 2, the more two similar nodes have relations in common, the less the retrieval error will be when the network is asked to generalize.
Whether this form of statistical generalization is a feature or a bug remains to be seen. In the case of instance nodes, generalization is an advantage, since many similar instances (e.g. of eating the same food regularly at the same restaurant -- normally represented as distinct symbols INGEST1, INGEST2... in symbolic systems) will be merged into a single prototype.
6. Other Symbol Recirculation Methods
Symbol recirculation is a relatively recent technique and thus the relative advantages and disadvantages of various recirculation methods are not well understood yet. The earliest symbol recirculation method that we are aware of was first described in (Miikkulainen and Dyer 1987). The method, subsequently called FGREP (Miikkulainen and Dyer 1988, 1989a), involves maintaining a global symbol memory, where each symbol is represented as a set of weights and where back propagation is extended into this global memory. FGREP was first used to learn distributed representations of lexical items, where a three-layer feed-forward PDP network is used to map a syntactic representation to a semantic representation. To learn the mapping task, back-error propagation is used, with the additional step of extending the back-error propagation weight update rule through the weights that connect a subset of the symbols (in the global symbol memory) to the input layer. For example, suppose the current mapping task contains the following two I/O pairs, where different syntactic roles must be mapped to different semantic case roles, depending upon the semantics of the words that are bound to the different syntactic roles.
I/O PAIR 1:
input banks: subject verb object prep-phrase
symbols JOHN EATS CHICKEN WITH FORK
output action actor instrument object obj-modifier
symbols EATS JOHN FORK CHICKEN XX
I/O PAIR 2:
input banks: subject verb object prep-phrase
symbols JOHN EATS HAM WITH CHEESE
output: action actor instrument object obj-modifier
symbols EATS JOHN XX HAM CHEESE
Table 3. Sample syntax-semantic mapping task
For I/O PAIR 1, back-propagation via FGREP results in modifying the weights that connect the symbols in the input layer the corresponding symbols in the global symbol memory. When the PDP network is called upon to learn I/O PAIR 2, the representations of JOHN, EATS, HAM and CHEESE are taken from the global symbol memory and their weights (from the global symbol memory to the input layer) are modified. As a result, each subsequent time the same I/O pair is presented to the mapping network, the representations of the symbols will be different. Over time, these representations will converge for a given training corpus. After training, the network shows better generalization to novel cases than with handcoded microfeature representations. In addition, the symbol memory forms representations in which symbols with similar uses (e.g. eating utensils, such as KNIFE, FORK, SPOON versus foods, such as HAM, CHICKEN) form similar representations. Ambiguous words shared representations across semantic categories (e.g. CHICKEN is animate in "FOX EATS CHICKEN", while CHICKEN is a prepared food in "JOHN EATS CHICKEN WITH FORK"). The FGREP method of symbol recirculation has since been generalized to recurrent PDP networks and FGREP modules have been formed into an architecture to dynamically acquire scripts and generate paraphrases of script-based stories (Miikkulainen and Dyer 1989b).
The method of extending back-propagation over PDP networks with more than three layers had been used prior to the work of Miikkulainen and Dyer. For example, Hinton (1986) used additional layers to form representations of family trees. However, Hinton did not save these representations in a global memory and then reuse and remodify them. Thus, the representations formed were not global (i.e. the input and output layers formed different representations) and also symbol recirculation did not occur.
Recently, Pollack (1988) has shown that a three-layer PDP network can learn stack and tree structures. In his method, called "recursive auto-association memory (RAAM)", a three-layer PDP network is given an autoassociative mapping task, in which the input/output layers have encoded in them the same pair of symbols. Once a symbol pair has been learned, say [A B], the pattern of activation on the hidden layer (call it C) is then used to represent the pair [A B]. To build up a tree structure, the network is now trained to autoassociate the pair [C D], where the pattern over its hidden layer now represents E = [C D]. Consequently, we have encoded the structure illustrated in figure 10.
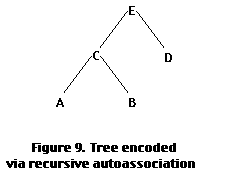
More recently, we have extended Pollack's RAAM technique. In our model (Lee et al. 1989), a number of RAAMs are augmented with a global lexicon. The distributed representation of a symbol, e.g. MILK, is gradually built up by training a recursive autoassociative network to learn a set of propositions concerning MILK, such as:
(COWS PRODUCE MILK)
(CHILDREN DRINK MILK)
(MILK HAS-COLOR WHITE)
...
As each triple is learned, the pattern of activation over the hidden layer is fed back into the position (a bank in the input layer) in the next triple in which MILK occurs. Once a stable pattern of activation for MILK has been formed, it is used in forming the distributed representation for all other symbols involving MILK, e.g. COWS, CHILDREN, WHITE, etc. This recirculation causes the representation for COWS to be modified, resulting in the need to recirculate MILK. After convergence has occurred for all symbols, each has encoded, within its pattern of activation, the structural information associated with it.
The related technique to the one presented in DUAL is that described in (Pollack 1987). Here, Pollack uses what he calls "cascaded" networks. Essentially, he links the output layer of one network to the connection weights of another network, thus forming higher-order connections. Pollack also shows how cascaded networks can receive feedback and thus form sequential cascaded networks. The resulting networks can learn finite state languages. Although many of the details are different, DUAL also uses this general technique of having one network manipulate the connection weights of another network.
7. Open Problems
There are many open problems, both in symbol recirculation and in representing semantic information in distributed connectionist networks. Two such problems are described here.
7.1. Convergence
The issue of convergence is central in DUAL networks. The nice features of symbol representations in DUAL will not be maintained if the symbol representation set in DSM does not converge. Unfortunately, there is no theoretic proof at this point for convergence in DUAL (or in other recirculation methods). Currently, there are three potential problems that can arise in DUAL:
(1) Oscillation -- The representation set for the handles oscillates and thus does not settle down to one consistent pattern.
(2) Degenerate Cases -- This problem occurs when all representations converge to identical patterns; e.g. 1101111. (Note. This degenerate representation set also satisfies our constraints.) Degeneration can occur when the initial handle set already carries some similarity in it and may be caused and/or aggravated by the way in which we normalize a weight matrix S
i when encoding it in the input layer of LTM.(3) Time problems -- For a small DUAL network (i.e. 8-bit long representations, 10 semantic nodes, 5 relationships per-node on average, and running 50 epoches) symbol recirculation usually takes around 8 hours CPU-time on a HP 9000/320 workstation.
When (1) and (2) occasionally arise, we have to start with a new set of initial handles to get around of the oscillation or degenerate case. Since DUAL makes use of back-error propagation during symbol recirulation, any problems in back-error propagation (e.g. local minima) will affect DUAL's performance.
For (3), we are currently working on a project to speed up the convergence procedure (when convergence occurs).
One might ask why the handles do converge in any case. Recall that the operation of autoassociating and compressing all S
i in LTM causes the hidden units to find an efficient encoding (Rumelhart and McClelland 1986) of the shared structure in each weight matrix Si. Although each weight matrix that performs a similar function may appear very different, what they share in common are the structural relations they encode at the semantic network level. It is this shared structure that is apparently being encoded in the hidden units of LTM. This shared structure then directs subsequent learning as the node representations are recirculated.7.2. Rules with Variables vs Statistical Associations
The preceding sections have discussed at length the dynamic formation of symbol representations. One very special type of symbol is one that plays the role of a variable. In order to implement rules, one needs both structure and variables. One major problem facing connectionist researchers is resolving the nature of statistical versus logical (rule-based) inferences. High-level cognitive tasks, such as NLP, require both the ability to make logical (rule-based) and statistically based inferences. Rumelhart and McClelland have pointed out the usefulness of statistically based inferences. For example, they suppose a PDP system has encountered many cases of babies interacting with objects in the world and then receives input "the baby kicked the ball". The network will automatically infer that the ball is large, light, and soft. It would be painful to have to anticipate and build in such inferences by hand, as rules of the sort:
if a baby kicks a ball
then the ball will be soft
Instead, we want such inferences to arise from the fact that most of the objects parents will allow a baby to encounter tend to be light, soft, and harmless. A nice feature of distributed connectionist systems is the ability to apply such experiences to a novel case, in the form of a statistically based associative generalization or conclusion.
On the other hand, actual rule-based inferences are also required. For example, we know the rule:
if x tells y message z
then y knows z
Though such a rule may have arisen from experiences with telling, the application of the rule is not biased by previous experiences. Furthermore, this rule will work for an infinite number of cases.
Standard PDP models are not capable of implementing a simple rule. Why is this the case? For example, consider the following rule, with 3 variables, that is represented as a relationship between two knowledge structures (schemas):
(TELL ACTOR X --> (KNOWS ACTOR Y
TO Y OBJECT Z)
OBJECT Z)
Imagine that a 3-layer PDP network is trained to associate instances of TELL frames (on the input layer) with KNOWS instances on the output layer. Here is a sample training set:
INPUT LAYER OUTPUT LAYER
John told Mary that Bill is sick. Mary knows that Bill is sick.
John told Fred that Bill is well. Fred knows that Bill is well.
John told Betty that Bill is sick. Betty knows that Bill is sick
Frank told George that Fred is well. George knows that Fred is well.
... ...
Upon learning such a training set, the network might be able to complete known patterns and, depending on the input representations, the network might even be able to generalize to some new cases. For instance, in the sample set above, males tell females that males are sick, but they tell males that males are well. So perhaps it will be able to generalize (even with some noise and/or incomplete patterns). E.g.:
INPUT LAYER OUTPUT LAYER
John told Gxxrge that Bill is xxx. George knows that Bill is well.
However, there are many problems with this implementation of a rule as a statistically based association. Two problems are:
1. Inability to handle novel symbols -- For instance, if we place a novel symbol (say "Glotz") in the TO slot of the TELL frame, then "Glotz" will fail to get propagated properly into the ACTOR slot of the KNOWS frame. Why is this the case? The network has never seen "Glotz" before; therefore, "Glotz" will be treated as a "noisy" version of a known pattern that is close to it in the input space. As a result, either mush (i.e. an intermediate pattern) will come out in the KNOWS:ACTOR slot, or, if the network is set up to complete mush to known patterns, then a known symbol (e.g. "Fred") will appear. In either case, the "Glotz" binding has failed to be propagated.
2. Inability to handle novel structures -- This problem is just an extension of the "novel symbol" problem. That is, no matter how many instances of the rule we train the network on, it will not handle completely novel instances. Remember, in a real rule, variables can be bound to any recursive structure. For example, given the novel input:
John told Frank that, although he had worked for months trying to lose weight, he was heavier than ever.
we want the system to conclude:
Frank knows that, although John has worked for months trying to lose weight, John is heavier than ever.
The PDP network that was trained on the cases where the message was "Male/female is well/sick" will be unable to generalize to messages about dieting. Since PDP implementations of rules are statistical in nature, they do not really create or propagate bindings. Without rules and virtual (unlimited) memory, there is no infinite generative capacity. Other problems with association-based models are discussed in (Dyer in press) and (Touretzky 1989).
8. Variable Binding Research and Symbol Formation
Although the problem of variable bindings has not yet been adequately solved for distributed connectionist systems, there are a number of researchers working on it.
Hinton and Touretzky (1985, 1988), for example, have addressed the problem of encoding semantic relations and implementing variables and bindings in a PDP architecture that operates as a production interpreter. In their case, instead of using a DUAL network approach, they encode the link r
j from Ai to Aj as a triple (Ai rj Aj) in the input layer. As a result, the entire semantic network can be encoded in a single PDP network.1 However, since there is no global symbol memory or recirculation method, the representations for their symbols remain static throughout processing.Dolan (1989) has constructed a PDP natural language processing architecture, based on tensors, which are a generalization of conjunctive coding techniques (Dolan and Dyer 1987, 1989). The use of tensors (Smolensky in press) and tensor manipulation networks (Dolan and Smolensky 1989) allows Dolan's system, CRAM, to dynamically bind and unbind symbols, through tensor outer products and dot products. The representations for each symbol, however, are static and prespecified as a set of microfeatures.
Sumida and Dyer (1989) have developed what they call "parallel distributed semantic" networks. Each semantic node consists of a layer of PDP units and specific instances of symbols can reside as a pattern of activation over a given PDP layer (semantic node). Although novel patterns are learned that represent instances of new episodes, the basic level symbols (e.g. from the lexicon) currently contain static representations.
Lange and Dyer (1989a, 1989b) have developed a method for using one type of activation (called "signature activation") to represent a binding. Basically, each symbol (e.g. JOHN) produces a constant activation value (e.g. JOHN = 4.3). To represent that the ACTOR of TELL is bound to JOHN, the activation value of 4.3. is propagated to that ACTOR node and causes that node to also produce a constant activation value of 4.3. Currently, the signatures are assigned initial values at random that remain the same throughout processing. A future research project is to dynamically form signature values through learning.
It is important to point out that the technique of symbol recirculation appears to be compatible with the symbol processing systems developed by researchers such as Dolan, Dyer, Hinton, Lange, Lee, Sumida, and Touretzky. That is, symbol recirculation could be used to dynamically form distributed symbol representations and then these symbols could be manipulated via PDP production interpreters and other distributed connectionist symbol processing architectures. This is an area of future research.
9. Summary and Conclusions
Using the insight that WMx = PoA (i.e. that weight matrices and patterns of activation are two sides of the same coin), we have designed and implemented DUAL, a PDP memory management architecture to encode and manipulate a symbolically specified semantic network as a virtual, distributed, directed graph in a PDP architecture. DUAL consists mainly of two PDP networks. The STM network functions as a working memory to temporarily hold all of given node's associations, while the LTM network functions as a long term memory for the entire semantic network. The process of encoding causes DUAL to find distributed representations for all nodes in the semantic network. As a result, nodes with similar associational links are merged and generalized. The DUAL architecture allows us to manipulate the virtual semantic network at a symbolic level, while at the same time retaining many of the robust features (of adaptive learning, generalization to novel cases, graceful error degradation, etc.) associated with distributed connectionist networks.
The method of automatic distributed symbol discovery in DUAL is an instance of a more general method, dubbed symbol recirculation, in which symbols start out with random patterns of activation and through the attempt of the system to form structural relations via associative mapping, new representations are formed. The resulting symbol representations are then actively involved in the operations that are demanded of them. Distributed representations of similar semantic nodes converge to similar representations, resulting in features exhibited by distributed connectionist networks, such as similarity-based generalizations to novel cases.
REFERENCES
Allen, R. B. Several Studies in Natural Language and Back-Propagation. Proceedings of IEEE First International Conference on Neural Networks. pp. II-335 - II-341, 1986.
Alvarado, S., Dyer, M.G. and M. Flowers. Editorial Comprehension in OpEd through Argument Units. Proceedings of American Association of Artificial Intelligence (AAAI-86), Philadelphia, PA pp. 250-256, 1986.
Alvarado, S. J., Dyer, M. G. and M. Flowers. Natural Language Processing: Computer Comprehension of Editorial Text. To appear in: H. Adeli (Ed.). Knowledge Engineering. McGraw-Hill, NY. (in press).
Churchland, P. S. and T. J. Sejnowski. Neural Representation and Neural Computation. In L. Nadel, L. A. Cooper, P. Culiver and R, M. Harnish (Eds.). Neural Connections, Mental Computation. Bradford Book/MIT Press, Cambridge, MA, pp. 1989.
Dolan, C. P. Tensor Manipulation Networks: Connectionist and Symbolic Approaches to Comprehension, Learning, and Planning. UCLA Ph.D. Dissertation, 1989.
Dolan, C. and M. G. Dyer. Symbolic Schemata, Role Binding and the Evolution of Structure in Connectionist Memories. Proceedings of the IEEE First Annual International Conference on Neural Networks. San Diego, CA, June 1987.
Dolan, C. P. and M. G. Dyer. Parallel Retrieval and Application of Conceptual Knowledge. In D. S. Touretzky, G. Hinton and T. Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summer School. Morgan Kaufmann, pp. 273-280, 1989.
Dolan, C. P. and P. Smolensky. Tensor Product Production System: a modular Architecture and Representation. Connection Science. Vol. 1, No. 1. pp. 53-68, 1989.
Dyer, M. G. In-Depth Understanding. Cambridge, MA: MIT Press, 1983.
Dyer, M. G. Symbolic NeuroEngineering for Natural Language Processing: A Multilevel Research Approach. In J. Barnden and J. Pollack (Eds.). Advances in Connectionist and Neural Computation. Ablex. Publishers, in press.
Dyer, M.G. Knowledge Interactions and Integrated Parsing for Narrative Comprehension. In D. Waltz (ed.), Advances in Natural Language Processing, LEA Press, Hillsdale, NJ. pp. 1-56, 1989.
Dyer, M.G., Cullingford, R. & Alvarado, S. SCRIPTS. In Shapiro (ed.) Encyclopedia of Artificial Intelligence. John Wiley & Sons, pp. 980-994, 1987.
Dyer, M. G., Flowers, M. and Wang, Y. A. (1988) "Weight-Matrix = Pattern of Activation: Encoding Semantic Networks as Distributed Representations in DUAL, a PDP Architecture" Technical Report UCLA-AI-88-5. CS Dept. UCLA, Los Angeles, CA. 1988.
Dyer, M.G. Reeves, J. and M. Flowers. A Computer Model of Irony Recognition in Narrative Understanding. Advances in Computing and the Humanities, Vol. 1, No. 1 (in press).
Dreyfus, H. L. and S. E. Dreyfus. Making a Mind Versus modeling the Brain: Artificial intelligence at a Branchpoint. pp. 15-43, In S. R. Graubard (Ed.). The Artificial Intelligence Debate: False Starts, Real Foundations. MIT Press, Cambridge MA, 1988.
Feldman, J. A. Neural Representation of Conceptual Knowledge. In L. Nadel, L. A. Cooper, P. Culiver and R, M. Harnish (Eds.). Neural Connections, Mental Computation. Bradford Book/MIT Press, Cambridge, MA, 1989.
Fodor, J. A. and Z. W. Pylyshyn. Connectionism and cognitive architecture: A critical analysis. pp. 3-71, In Pinker and Mehler (eds.) Connections and Symbols, Bradford books/MIT Press, 1988.
Gasser, M. A Connectionist Model of Sentence Generation in a First and Second Language. UCLA Ph.D. and Technical Report UCLA-AI-88-13, July 1988.
Gasser, M. and M. G. Dyer. Sequencing in a Connectionist Model of Language Processing. Proceedings of Twelfth Intern. Conf. on Computational Linguistics (COLING-88). Budapest, Hungary. pp. 185-190, 1988.
Hendler, J. A. Integrated Marker-Passing and Problem Solving: A spreading activation approach to improved choice in planning. LEA Press, Hillsdale NJ, 1987
Hendler, J. Spreading Activation over Distributed Microfeatures. In D. S. Touretzky (Ed.) Advances in Neural information Processing Systems 1, 553-559, Morgan Kaufmann Publisher, CA, 1989.
Hinton, G. E. Learning Distributed Representations of Concepts. Proceedings of the Eighth Annual conference of the Cognitive Science Society., pp. 1-12, Amherst, MA. 1986.
Lange, T. E. and M. G. Dyer. Dynamic, Non-Local Role Bindings and Inferencing in a Localist Network for natural Language Understanding. In D. S. Touretzky (Ed.) Advances in Neural Information Processing Systems 1, pp. 545-552, Morgan Kaufmann Publisher, CA, 1989a.
Lange, T. E. and M. G. Dyer. High-Level Inferencing in a Connectionist Network. Connection Science, Vol. 1, No. 2, 1989b.
Lee, G., Flowers, M. and M. G. Dyer. A Symbolic/Connectionist Script Applier Mechanism. Proceedings of the Eleventh Annual Conference of the Cognitive Science Society (CogSci-89). Ann Arbor, Michigan, pp. 714-721, 1989.
McClelland, J. L. and Kawamoto, A. H. Mechanisms of Sentence Processing: Assigning Roles to Constituents of Sentences. In McClelland and Rumelhart (eds.) Parallel Distributed Processing, Vol. 2. 1986.
Miikkulainen, R. and Dyer, M. G. Building Distributed Representations without Microfeatures. Tech. Rep. UCLA-AI-87-17, Computer Science Dept. UCLA, August 1987.
Miikkulainen, R. & Dyer, M. G. Forming Global Representations with Extended Backpropagation. Proceedings of the IEEE Second Annual International Conference on Neural Networks (ICNN-88), San Diego, CA. pp. I-285 - I-292, July 1988.
Miikkulainen, R. and M. G. Dyer. Encoding Input/Output Representations in Connectionist Cognitive Systems. In D. S. Touretzky, G. Hinton and T. Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summer School. pp. 347-356, Morgan Kaufmann, 1989a.
Miikkulainen, R. and M. G. Dyer. A Modular Neural Network Architecture for Sequential Paraphrasing of Script-Based Stories. Proceedings of the International Joint Conference on Neural Networks (IJCNN-89). pp. II-49 - II-56, Wash. D.C. June, 1989b.
Pinker, S. and and Prince, A. On Language and Connectionism: Analysis of a Parallel Distributed Processing Model of Language Acquisition. In Pinker and Mehler (eds.) Connections and Symbols, Bradford books/MIT Press, pp. 73-193, 1988. (Special issue of Cognition: An International Journal of Cognitive Science, Vol. 28)
Pollack, J. Recursive Auto-Associative Memory: Devising Compositional Distributed Representations. Proceedings of the Tenth Annual Conference of the Cognitive Science Society. Montreal, pp. 33-39, 1988.
Pollack, Jordan B. Cascaded Back-Propagation on Dynamic Connectionist Networks. Proc. of Ninth Annual Conference of the Cognitive Science Society, pp. 391-404, Seattle Wash. 1987.
Quilici, A., Dyer, M. G., and M. Flowers. Recognizing and Responding to Plan-Oriented Misconceptions. Computational Linguistics, Vol. 14, No. 3, pp. 38-51, 1988.
Reeke Jr., G. N. and G. M. Edelman. Real Brains and Artificial Intelligence. In S. R. Graubard (Ed). The Artificial Intelligence Debate: False Starts, Real Foundations. MIT Press, Cambridge MA, pp. 143-173, 1988.
Reeves, J. F. Ethical Understanding: Recognizing and Using Belief Conflict in Narrative processing. Proceedings of the Seventh National Conference on Artificial Intelligence (AAAI-88). Saint Paul, MA, pp. 227-232, 1988.
Rumelhart & McClelland. Parallel Distributed Processing. Vols. 1 and 2, Cambridge, MA: MIT Press/Bradford Books, 1986.
Rumelhart, D. E. and J. L. McClelland. On Learning the Past Tense of English Verbs. In Rumelhart & McClelland. Parallel Distributed Processing. Vol. 2, Cambridge, MA: MIT Press/Bradford Books, pp. 216-271, 1986a.
Rumelhart, D. E. and McClelland, J. L. Learning Internal Representations by Error Propagation. In Rumelhart & McClelland Parallel Distributed Processing. Vol. 1, Cambridge, MA: MIT Press/Bradford Books, pp. 318-362, 1986b.
Sejnowski, T. J. and C. R. Rosenberg. Parallel networks that learn to pronounce English text. Complex Systems 1: 145-168, 1987.
Shastri, L. A Connectionist Approach to Knowledge Representation and Limited Inference. Cognitive Science 12: 331-392, 1988.
Smolensky, P. On the proper treatment of connectionism. The Behavioral and Brain Sciences, Vol. 11, No. 1, pp. 1-23, 1988a.
Smolensky, P. The Constituent Structure of Connectionist Mental States: A Reply to Fodor and Pylyshyn. In T. Horgan and J. Tienson (eds.) Connectionism and the Philosophy of Mind, Department of Philosophy, Memphis State University, pp. 137-161, 1988b. (The Southern Journal of Philosophy, 1987, Vol. XXVI, Supplement).
Smolensky, P. Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence, in press.
Sumida, R. A. and M. G. Dyer. Storing and Generalizing Multiple Instances while Maintaining Knowledge-Level Parallelism. Proceedings of Eleventh International Joint Conference on Artificial Intelligence (IJCAI-89). Detroit, Michigan. pp. 146-152, August 1989
Sutton, R. S. Temporal Credit Assignment in Reinforcement Learning. Ph.D. Dissertation, University of Massachusetts, 1984.
Touretzky, D. S. and Hinton, G. E. A Distributed Connectionist Production System. Cognitive Science, Vol. 12, No. 3, pp. 423-466, 1988.
Touretzky, D. S. Connectionism and PP Attachment. In D. S. Touretzky, G. Hinton and T. Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summer School. Morgan Kaufmann, pp. 325-332, 1989.