Distributed Symbol Formation and Processing
in Connectionist Networks
Michael G. Dyer
*3532 Boelter Hall
Computer Science Department
University of California, Los Angeles CA 90024
(e-mail: Dyer@cs.ucla.edu)
(office: (213)455-1291; secr: 825-2303)
Abstract
Distributed connectionist (DC) systems offer a set of processing features which are distinct from those provided by traditional symbol processing (SP) systems. In general, the features of DC systems are derived from the nature of their distributed representations. Such representations have a microsemantics -- i.e. symbols with similar internal representations tend to have similar processing effects. In contrast, the symbols in SP systems have no intrinsic microsemantics of their own; e.g. SP symbols are formed by concatenating ASCII codes that are static, human engineered, and arbitrary. Such symbols possess only a macrosemantics -- i.e. symbols are placed into structured relationships with other symbols, via pointers, and bindings are propagated via variables. The fact that DC and SP systems each provide a distinct set of useful features serves as a strong research motivation for seeking a synthesis. What is needed for such a synthesis is a method by which symbols can dynamically form their own microsemantics, while at the same time entering into structured, recursive relationships with other symbols, thus developing also a macrosemantics. Here, we describe a general method, called symbol recirculation, for allowing symbols to form their own microsemantics. We then discuss three techniques for implementing variables and bindings in DC systems. Finally, we describe a number of DC systems, based on these techniques, which perform a variety of high-level cognitive tasks.
1. Introduction: Distributed Connectionism vs. Symbolism
High-level cognitive tasks, such as natural language processing (NLP), require the constituent structures, systematicity, and rule-governed behavior (Pinker and Prince 1988) (Fodor and Pylyshyn 1988) that are supplied by traditional symbol processing (SP) systems (Newell 1980). However, systems constructed within the SP paradigm, e.g. (Dyer 1983), tend to be fragile (i.e. poor noise and fault tolerance) and suffer from a knowledge engineering bottleneck (i.e. the need to construct vast amounts of knowledge by hand). Distributed connectionist (DC) systems (Rumelhart and McClelland 1986) (Touretzky and Hinton 1989) are appealing because they offer the hope of overcoming the fragility and knowledge bottleneck problems that plague SP systems (Smolensky 1988a) (Churchland and Sejnowski 1989) (Dyer in press).
1.1. Attractive Features of Distributed Connectionist Models
The distributed connectionist paradigm involves the use of very simple processing units (e.g. summation of inputs plus sigmoidal or other thresholding function) which are highly interconnected and communicate via spreading activation/inhibition. Short-term information in DC systems is represented by the level of activity of either a single processing unit (i.e. "localist" representations) or by a pattern of activity over a set of processing units (i.e. "distributed" representations). Long-term information is represented in terms of the connectivity pattern between processing units, where each connection is variably weighted. These "weights" alter (usually via multiplication) the activation values sent between processing units. Connection weights may be set by hand (i.e. creating "structured" networks) or modified automatically by adaptive learning algorithms, e.g. via back-propagation in "PDP" networks (Rumelhart and McClelland 1986). The distributed connectionist paradigm is of interest because of the attractive features that many DC models exhibit, namely:
(a) Automatic learning and generalization: Learning is so fundamental to these models that they are not really programmed (in the algorithmic sense) but modify their behavior as the result of supervised training or reinforcement. Instead of induction over a preexisting symbol vocabulary, connectionist models learn through incremental adaptation in the face of repeated interaction with a set of input/output mappings. By local modification of connection weights, such models categorize the data such that novel inputs can be handled, based on a generalization of the statistical structure that has been extracted from the training set.
(b) Associative memory, massive parallelism and fault tolerance: Complete memory patterns can be generated from fragmentary and noisy cues in the input. In contrast, in symbolic models one must explicitly decide how a symbolic structure will be indexed for retrieval. Connectionist models also exhibit smooth degradation in the face of 'lesions' (removal of processing units and alteration of connection weights).
(c) Smooth parallel constraint satisfaction: The expectations generated by connectionist models are statistical in nature, and the model finds a memory based on satisfying a large number of soft constraints in parallel. The process is one of settling into a minimal energy state, rather than generating a proof path through the chaining of rules. Rather than viewing "soft" behavior as arising through the interaction of a great number of "hard" rules, connectionists predict that "hard" behavior will emerge through the interaction of a great number of "soft" constraints (Smolensky 1988b).
(d) Neural plausibility: In addition, connectionist models are loosely inspired by what is known about real nervous systems, and thus hold out the potential of linking mind to brain at some future date (Churchland 1986).
(e) Reconstructive memory: Since all long-term memories are encoded in the connection weights, memories are shared over the same hardware. Thus, retrieval is more a matter of reconstructing a memory than going to a discrete location to find it. As new memories are added to connectionist models, they can exhibit retroactive interference, but repetition of the original data will reestablish the older memories. If the same amount of repetition were required, then such models would not be so interesting. However, a recent study (Hetherington and Seidenberg 1989) indicates that less repetition is required during relearning. Thus, the most effective learning strategy in such models (i.e. train via repetition; learn something new; then briefly retrain on the earlier material) seems to parallel similar aspects of learning in children. In contrast, phenomena of forgetting and memory confusions (Bower et al. 1979) have only been explained in symbolic models through the loss of pointers or the reorganization of other indexing structures (Schank 1982). Connectionist models, however, explain forgetting and confusions in a very natural way, through interference over shared hardware.
These features are due mainly to the nature of the representations being encoded and manipulated in DC networks, where representations are distributed (Hinton et al. 1986) over many simple processing elements and properties of the model are "emergent phenomena" from the interaction of a great many elements.
1.2. Attractive Features of Symbolic Processing Systems
In spite of the attractive features of DC systems, it is difficult to get such systems to perform high-level cognitive tasks (such as NLP), because of the lack of many of the features supplied by symbol processing systems, namely:
(a) Tokens and types: In symbolic systems, one can dynamically create instances (e.g. HUMAN13) that can be kept distinct from the general type (HUMAN). In connectionist systems, it is easy to form types, but difficult to keep instances straight, e.g. connectionist models suffer from "cross-talk" (Feldman 1989).
(b) Inheritance: Given types and tokens, one can update a type (e.g. learn that HUMAN --ISA--> MORTAL) and immediately this fact is deducible for all relevant tokens that are instances of that type.
(c) Virtual reference: One symbol structure can point to another structure that resides at a distant location in physical memory, thus supporting the creation of complex virtual memories without having to reorganize physical memory. In fact, it is this virtual memory capability that allows current von Neumann machines to simulate any connectionist model. In contrast, it is unclear how a pattern in one region of a connectionist memory could refer to patterns in physically distant regions. Suppose one region of memory contains the schema instance (BELIEVES (ACTOR JOHN) (ROBBED (ACTOR FRED) (OBJECT CAR) (FROM JOHN)), we would like to have the system build a representation (ANGRY (ACTOR JOHN) (AT FRED)). In a symbol model, we can simply bind the ACTOR of an instance of the ANGRY schema with a pointer to JOHN. In DC models, the propagation of such dynamic bindings is problematic.
(d) Structure and compositionality: Given pointers, complex recursive structures can be built "on the fly" and used to represent the recursive and constituent structures exhibited by the embedded syntax and semantics of NL grammar and concepts (e.g. "John told Mary that Bill promised Fred that he would mow the lawn."). Symbolic systems are also able to take separate facts and rules and then combine them to produce a potentially infinite number of new structures, through repeated composition of structure. In contrast, connectionist systems have great difficulty combining two distinct sources of knowledge to perform novel tasks, e.g. see discussion by Touretzky (1989).
(e) Variables and structure sensitive operations: With variables and structure, one can specify, for an infinite number of possible instances, how knowledge is to be propagated and instantiated from one structure to another; e.g., one can specify that ((x SELLS obj TO y FOR-COST z) --results--> (AND (OWNS y obj) (OWNS x (MONEY AMOUNT (PREVIOUS MINUS z)))). This rule will work for any owner, object and cost. In connectionist models, one can only approximate such rules, by training the network on a large number of instances of the rule. These instances will influence subsequent generalizations, but logical inferences are able to function independently of the statistical structure inherent in any particular training set.
(f) Communication and control: In structure manipulating languages, such as LISP, what one function produces can be interpreted by any other function. This is the case because every LISP function has access to, and uses, the same structure-building and structure-traversing primitive operations (e.g. CONS, CAR, CDR). Such operations allow one function to communicate its results to other functions, thus supporting parallelism and communication at the structural level. In contrast, it is unclear how the connection weights developed through learning in one network can be used by another network. Current connectionist models have only primitive communication and control architectures.
(g) Memory management: In symbolic systems there is always a function that will supply "raw" memories on request, for the run-time construction of episodes. Such functions (e.g. GENSYM and MAKSYM in LISP) allow one to build new memories from old memories and new input. In connectionist models, however, the number of processing units is fixed at the onset. For example, if there are too few hidden units, then the network will not be able to learn the training data. But if there are too many hidden units, then the network will simply memorize the training data without forming the shared representations that support generalizations to new inputs. Connectionist systems need to incorporate a theory of how weakly active '"neurons" become "recruited" (Diederich in press) (Srinivas and Barnden 1989) as the need for new memories grows or as new tasks are learned.
It is difficult to handle the counterplanning strategies of agents in narrative text or the argument and belief structures in editorial text when one is lacking recursive data structures, pointers, variables, instantiation, unification, rules, inheritance, etc. For example, when I first started out to reimplement NLP in connectionist networks, I quickly discovered that I could not even encode my (variable length) natural language input properly on the (fixed width) input layers of feedforward PDP networks.
1.3. Von Neumann Symbols versus DC Symbols
While variables and propagation of bindings are critical features of symbolism, the symbols in von Neumann architectures have no intrinsic microsemantics of their own; e.g. symbols are formed by concatenating ASCII codes that are static, human engineered, and arbitrary. To gain a macrosemantics, these arbitrary and static bit vectors are placed into structured relationships with other arbitrary symbols, via pointers. In contrast, symbols in connectionist systems can be represented as patterns of activity over a set of processing units and these patterns can directly have semantic significance. For example, when these patterns are placed onto the input layer of a connectionist network, they cause the reconstruction of patterns in the output layer(s) where the kind of output produced depends critically on the nature of the input patterns.
In the brain it is probably not the case that symbols consist of static or arbitrary codes. It is more likely that, for example, in a child the representation for DOG (i.e. dogs in the abstract), is dynamically formed through many interactions with numerous dogs. Later, the abstract concept DOG, when combined with specific cues, will cause the reconstruction of visual and other sensory experiences of a specific dog. Thus the concept DOG is grounded (Harnad 1987, 1989) in perceptual experience. At the same time, the concept of DOG must be invariant with respect to any particular sensory experience, since one can learn facts about dogs in general (e.g. that they are animals) and relate these facts to one another for high-level reasoning. Humans are also capable of learning facts about specific instances of a general class. For example, we can store information that John's dog, Fido, bit his neighbor.
2. Distributed Symbol Formation through Symbol Recirculation
What we want is a method by which each symbol dynamically forms its own microsemantics, while at the same time entering into structured, recursive relationships with other symbols. A general technique for accomplishing this goal we call symbol recirculation. In this technique, symbols are maintained in a separate connectionist network that acts as a global symbol lexicon (GSL), where each symbol is composed of a distributed pattern of activation. Symbol representations start out as random patterns of activation. Over time they are "recirculated" through the symbolic tasks being demanded of them, and as a result, gradually form distributed representations that aid in the performance of these tasks. Symbol representations arise as a result of teaching the system to form associative mappings among other symbols, where these mappings capture structured relationships.
The basic technique of symbol recirculation involves: (1) starting with an arbitrary representation for each symbol in the GSL, (2) loading these symbols into the input/output layers of one or more DC networks, where each network is trained to perform a given mapping task, (3) modifying the symbol representations in the GSL to aid the mapping network(s) in the performance of the task, while at the same time modifying the connection weights of these networks, (4) storing the modified symbol representations back into the global symbol lexicon as patterns of activation, and (5) iterating over all symbols, DC networks, and tasks until all symbol representations have stabilized for all tasks.
Symbol recirculation is possible because the same vector of values can be viewed at any moment in time as specifying either a set of weights, for modification during learning, or as a pattern of activation to be fed as input/output to some network. Symbol recirculation can also be viewed as a stylized method for implementing and modifying higher-order connections, in which a connection in one network gates a connection within another network.
In previous connectionist networks, the connection weights of the DC mapping networks were modified, but the encoding of representations themselves -- i.e. representations on the input and output layers, which represent the training set -- remained unchanged. With symbol recirculation, however, the representations of the training set are undergoing modification while the task (which involves forming mappings between those representations) is being learned.
2.1. Three Methods for Symbol Recirculation
At the UCLA AI lab we have been exploring three methods of symbol recirculation: FGREP, DUAL and XRAAM. All three methods involve the use of a GSL that is separate from the architecture being used to learn a given task. Symbols are taken from the GSL and loaded into the input and output layers of the DC architecture. These strings of symbols then represent the I/O pairs the architecture is learning to associate.
2.1.1. Extending Backpropagation into Symbols with FGREP
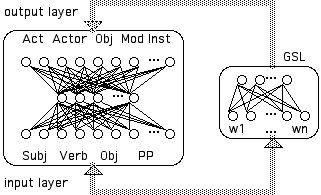
In the FGREP method (Miikkulainen and Dyer 1988, 1989a), each symbol is represented as a pattern of weights in a GSL. The values of these weights are placed into one or more case-role ensembles in both the input and output layers of one or more associative networks. To modify the representations of the symbols as they are used, back-error propagation (Rumelhart et al. 1986) is extended into the GSL -- i.e. into the weights representing the symbols being used. These new symbol representations are then used to represent other I/O mappings in the training data. The basic architecture is shown in Figure 1, which shows the FGREP method being applied to the task of associating syntactic case-roles (subject, verb, object, prepositional phrase, etc.) with semantic case-roles (Act, Actor, Object, Modifier, Instrument, etc.).

Figure 1:
FGREP Method applied to task of mapping NL syntax to semantics. Symbols (w1...wn) in GSL are placed into syntactic segments (Subj, Verb, etc.) of input layer and into semantic segments (Act, Actor, etc.) of output layer. Weight changes (for each symbol used) are backpropagated into the GSL, thus modifying the (initially random) representations of each symbol in GSL.To learn the syntax-to-semantics mapping, the connection weights in the association network are modified via backpropagation. In addition, that portion of the GSL, which was loaded into the input layer, is viewed as an additional layer, extending from the input layer into the GSL. Backpropagation can then be extended into this portion of the GSL, causing those symbol representations to be modified. Later, when a new mapping is to be learned, the modified GSL representations will be loaded into both the input and output layers of the association network. Notice that, each time the same symbol is selected from the GSL, it will have a different representation; thus, the training environment is undergoing modification (i.e. the representation of a given I/O pair changes throughout the training). Consequently, the training environment is reactive.
2.1.2. Manipulating Weights as Activations in DUAL
In the DUAL method (Dyer et al. in press), the architecture consists of a short-term memory (STM) and a long-term memory (LTM), along with a GSL. See Figure 2 for an overview of the DUAL architecture.
A set of slot/value pairs, representing a given frame/schema (Minsky 1975), are learned by the STM (via backpropagation). The representations of each STM filler are initially random. The resulting STM weights (from the input to hidden layer and from the hidden to output layer) are loaded into the input (bottom) layer of the LTM, where they are autoassociated with the LTM's output layer.
The pattern formed over the LTM hidden layer is a compressed representation of an entire schema of slot/filler pairs and is placed in the GSL. When the slot of one frame F1 points to another frame F2 as its value, then the pattern of activation representing F2 is taken from the GSL and placed in the output layer of STM and the weights in STM are modified to learn that slot/filler association. These modified weights are then placed back into LTM and the new representation for F1 is placed back into the GSL. To reconstruct the slot/filler properties associated with, say, frame F1, the F1 distributed symbol is taken from the GSL and placed into the hidden layer of LTM, which causes LTM to reconstruct a pattern on its output layer. This pattern can then be used to modify all of the weights in STM. STM will now represent frame F1.
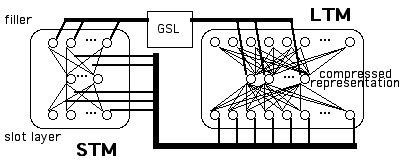
Figure 2:
DUAL Method. STM is trained to associate a slot name (property) on the input layer with a filler (value ) on the output layer. LTM is an autoassociative memory. The number of STM weights equals the number of input/output units in LTM. The number of hidden units in LTM equals the number of input/output units in STM. GSL holds symbols representations that were formed in the hidden layer of LTM.
For example, assume that we want to encode two, simple frames below:
(JOHN1
(F-NAME JOHN)
(GENDER MALE)
(OCCUPATION DOCTOR)
(LOVES MARY1))
(MARY1
(F-NAME MARY)
(GENDER FEMALE)
(OCCUPATION PROFESSOR)
(LOVES JOHN1))
Notice here that each frame points to the other, thus forming a network. To encode the JOHN1 frame, we train STM to associate F-NAME on the input with JOHN on the output layer, GENDER with MALE; OCCUPATION with DOCTOR, and LOVES with the symbol representation for MARY1. The STM weights are then loaded into LTM and compressed into the hidden layer. This compression then replaces the (initially arbitrary) symbol representation for JOHN1 in the GSL. To retrieve any fact about JOHN1, we can reconstruct the STM weights in the LTM output layer by placing the JOHN1 pattern in the LTM. Once LTM output is loaded into STM weights, we can retrieve any portion of the JOHN1 frame; e.g. we can access John's occupation by placing OCCUPATION in the STM input layer and by reading off the pattern reconstructed on the STM output layer.
In these frames, JOHN1 loves MARY1 and MARY1 loves JOHN1, so each symbol’s meaning depends on the meaning of the other. Consider how the representation of the mapping (LOVES MARY1) is formed while the JOHN1 frame is being encoded. Initially, MARY1 is a random pattern, taken from the GSL, so LOVES will be associated with this random pattern. Later, however, the MARY1 frame will be encoded in LTM; therefore, a new representation for MARY1 will be placed in GSL. As a result, the LOVES slot in the JOHN1 frame 'points to' the wrong representation for MARY1. The JOHN1 symbol in GSL must therefore be modified, by associating in STM the JOHN1 slot-fillers, e.g. (LOVES MARY1), with the correct MARY1 representation. But this process will alter the representation for JOHN1, thus requiring the slot-filler (LOVES JOHN1) in the MARY1 frame to be recirculated. This symbol recirculation process continues until the representations for all the symbols in the GSL have stabilized (e.g. until John and Mary each "love the correct representations for each other").
2.1.3. Using Extended Recursive Autoassociation to form Distributed Semantic Representations
The XRAAM method (Lee et al. 1989), makes use of the recursive autoassociative memories (RAAMs) originally developed by Pollack (1988), but in this case, the RAAM is augmented with a GSL. In the XRAAM (extended RAAM) method, a PDP network is trained to autoassociate a [predicate slot value] pattern on the input and output layers. The resulting pattern of activation on the hidden layer is then placed in a GSL and represents the predicate. See Figure 3 for an overview of the architecture.
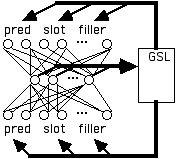
Figure 3:
XRAAM Method, based on Pollack’s RAAMs. Compressed representation in the hidden layer of units is placed in GSL and later fed back into one of the roles in the input/output layers.For example, suppose we want to form a distributed symbol for MILK. We load from GSL the following triples into the XRAAM network:
MILK HAS-COLOR WHITE
MILK CLASS LIQUID
MILK PRODUCED-BY COW
... ...
As each autoassociation is learned, we place the compressed pattern (from the hidden layer of the autoassociation network) into the GSL as the new representation for the predicate of the triple. Then we reuse this pattern to represent MILK in the subsequent [predicate slot value] triples being learned. As a result, a distributed representation for MILK is slowly formed and will serve to reconstruct information associated with it. For example, given the partial pattern [MILK PRODUCED-BY xxxx], a decoding XRAAM network can reconstruct the pattern COW. Of course, COW itself is a symbol whose (initially arbitrary) representation is taken from the GSL. Like all other symbols in the GSL, COW has also been dynamically formed by triples, such as:
COW #-LEGS FOUR
COW PRODUCES MILK
COW SOUND MOO
Based on the XRAAM method, a system, DYNASTY (Lee et al. 1989), has been built that was trained to learn script-based symbols and lexical entries. DYNASTY can generate paraphrases of script-based stories it has read.
2.2. Distributed Symbols Form a Microsemantics
As a result of these symbol recirculation methods, the symbols formed have their own "microsemantics". In the DUAL case, if two frames, say JOHN1 and BILL1, have nearly identical slot-fillers (e.g. same GENDER, OCCUPATION, AGE, etc.), then the representations for JOHN1 and BILL1 will be nearly identical. Suppose that BILL1 has one additional slot-filler, say (HAS-PET CAT) that the JOHN1 frame is lacking. Suppose we query the JOHN1 network with HAS-PET. Since JOHN1's representation is similar to BILL1's, the output by DUAL will consist of a pattern that is closest to CAT. Thus, DUAL can generalize to novel cases, based on the statistics inherent in the data used to create the frames in DUAL's memory (Dyer et al. in press).
The use of XRAAM and FGREP each have similar effects. For example, in the natural language understanding tasks for which FGREP has been applied, words with similar semantics (as defined by word usage) end up forming similar distributed representations in the lexicon (Miikkulainen and Dyer 1989a,b). Figure 4 shows the initial and final states of distributed representations for four words. Initially, their patterns are random and unrelated. After many iterations, words used identically have identical representations and words used nearly identically have formed very similar representations.
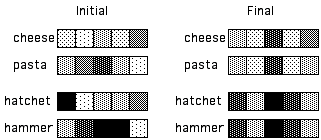
Figure 4:
Each word is represented as a distributed pattern of continuous values.If two words are used identically, their representations will converge. However, as their uses diverge, so also will their representations. Ambiguous words end up producing composite representations, sharing activity profiles with both classes/uses from which their meanings are drawn. For example, if "sofa" and "couch" are used interchangeably in all of the training data, then their representations will become identical. However, if they differ slightly in use (e.g. the data contains "sofa bed" but never "couch bed"), then the representations will also be slightly different. An ambiguous word (e.g. "bat" can be either a live animal or a wooden pole) will have representations that share patterns with words from the semantic classes to which the ambiguous word is related.
One can also perform a merge cluster analysis (Kohonen 1982) on the words in the GSL and optimal clusters are formed, related to word semantic/syntactic use (figure 5).
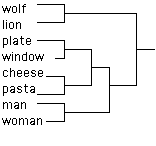
Figure 5:
Clusters with the shortest euclidian single linkage distance are merged. Here, all nouns form one cluster. Animals and humans form two related subclusters, while inanimate objects (i.e. breakable objects and foods) form two other separate, related subclusters. The particular results depend on the statistical structure inherent in the training data.The use of symbol recirculation results in systems with superior generalization and tolerance to noise and 'lesioning' (Miikkulainen and Dyer 1988, 1989a). In earlier PDP models for NLP, the representations of the training data were created by hand, through the use of microfeatures (McClelland and Kawamoto 1986). These microfeature-based representations remain static throughout the training. With symbol recirculation, however, the system finds its own representations for the training data while at the same time adjusting it connection weights in the association network(s). Since symbols used in similar ways have formed similar representations, the total knowledge of the system is distributed across both the global symbol lexicon (which is used to form the I/O) and the connection weights in the various association networks, which are being trained to perform the tasks at hand.
The resulting theory of word semantics in distributed connectionist models is very different from that of traditional NLP, in which (a) word meanings are represented in terms of hand-coded symbolic structures, (b) expectations consist of explicit, attached rules, e.g. (Dyer 1983), and (c) lexical acquisition occurs as the result of applying inductive, rule-based heuristics, e.g. (Zernik and Dyer 1987). In contrast, FGREP words consist of patterns of activation, formed automatically, through interaction with the data, and expectations are smooth and statistical in nature. That is, as each word is loaded into the case roles in the input layer, a pattern gradually forms across all case-roles in the output layer. With symbol recirculation, word representations are automatically formed through word use and word acquisition is viewed more as skill acquisition than acquisition of discrete facts and relationships. As a result of this learning, the representation of each word carries a memory trace of all the contexts of use that serve to define it.
3. Connectionist Methods for Creating Variables and Propagating Bindings
It is not sufficient to form distributed representations that both have a microsemantics and encode constituent structure. To realize symbol processing, one must also be able to implement rules with variables and dynamically propagate bindings. In symbolic systems, this capability is achieved through the use of pointers, which create virtual references between elements of conceptual memory that reside at distant sites in physical memory. Dynamic bindings are essential for implementing logical rules and propagating information. Consider the following simple rule:
R1: (TELL (ACTOR x) (MSG y) (TO z)) ===> (KNOW (ACTOR z) (MSG y))
R1 encodes the knowledge that once x tells y some message, y will know that message. To implement R1, a network must be able to propagate, without alteration, the bindings in the TELL schema to the corresponding binding sites in the KNOW schema. Due to the variables x, y and z, the rule R1 will work for any structures bound to these variables.
A very different type of inference is one that is statistically based. For instance, in PDP networks (Rumelhart and McClelland 1986), one can train the input layer of the network with instances of the left-hand side of the above rule and the output layer with the corresponding right-hand side. Suppose the majority of the training pairs have an implicit statistical structure, say, that whenever females tell males something the message tends to be that the females are hungry. If this is (statistically) the case, then the network will infer (i.e. generalize) for a new instance (e.g. Mary telling John) that Mary is hungry. This kind of statistically based inference is very nice to have, since it adds a "richness" (what Elman (1989) calls "context sensitivity") to the representation of each telling experience. However, statistically based techniques appear to be incapable of handling totally novel inputs, such as "Mary told John that her bicycle has a flat tire". Here, the message has nothing to do with previous messages encountered, so a statistically based approach will not work. A system with logical inferential ability, however, can handle this message equally well, concluding correctly that John now knows that Mary’s bicycle has a flat tire. This conclusion occurs independent of the number and/or content of past telling (or past bicycle) experiences known to the system.
One method of solving the problem of dynamic binding propagation is to augment connectionist networks with propagation of markers, e.g. (Charniak 1986; Hendler 1988; Sumida et al. 1988), which are data structures containing symbolic pointers. However, a symbolic pointer implies that there is an underlying symbol processing architecture (e.g. von Neumann machine with addressing by location) available at every node in the connectionist network. This approach thus defeats one of the major goals of connectionism, which is to implement cognitive processes in networks of simple processing units that, although perhaps highly abstracted, are still functionally related to the known properties (and limitations) of real neurons. Thus, a major task facing connectionism is the creation and propagation of bindings. Currently, there are three distributed representations that we have been exploring, which support the process of variable binding. These are: tensor representations, Content+ID representations and signatures.
3.1. Tensor Manipulation Networks
In (Rumelhart and McClelland 1986), one page (Hinton et al. 1986, p. 90) is devoted to conjunctive coding, a method in which an association between two binary vectors, X and Y (say, each of size n) are stored by allocating n2 processing units (i.e. a 2-dimensional plane) of memory. The pattern for X is placed across one dimension of the plane and then that pattern is repeated in the other dimension wherever the vector Y has a nonzero value. Hinton et al. point out that, while this method is expensive in the number of units required, it does solve the binding problem, since, given X, one can extract Y and vice versa. We did a number of experiments using conjunctive coding (Dolan and Dyer 1987, 1989) to represent bindings for natural language processing tasks. During that time, we discovered that Smolensky (1987) had generalized conjunctive coding to the use of tensors, which allow nonbinary values and the use of memories of arbitrary dimension. Recently, Dolan has applied Smolensky's tensor approach to build CRAM, a hybrid connectionist/symbolic natural language understanding system. CRAM reads and extracts novel planning advice from Aesop's Fables (Dolan 1989). In the tensor method, bindings between vectors X and Y are represented as the tensor outer product of two vectors and bindings can be extracted through the use of inner product operations. CRAM uses 3-dimensional tensors to represent [frame slot value] structures and employs 5-dimensional tensors to represent bindings across frames. However, as many mappings are overlaid into the same tensor, cross-talk occurs (Feldman 1989). Cross-talk is the creation of spurious bindings, due to the overlaying of memories. Dolan has had to create specialized circuits in order to extract bindings in the face of cross-talk. One interesting result is that cross-talk is eliminated more efficiently in CRAM as more knowledge is added to discriminate frames encoded within CRAM's memory. As a result, CRAM's accuracy of recall can improve as it acquires more knowledge (Dolan 1989).
Symbolic systems supply architectures so that symbols can be propagated without alteration. The result is that novel symbols can be passed about trivially, but the symbols lack a microsemantics. Connectionist architectures can dynamically form symbols with a microsemantics, but have difficulty propagating patterns without alteration, due to the modification of patterns of activation as they are passed through various weight and thresholding networks. Thus, there is a tension between (a) the need to make logical inferences, by not altering bindings as they are propagated, and (b) the need to alter patterns of activation as they are passed along, in order to make use of the statistical knowledge encoded in the weights of connectionist networks. There currently appear to be two approaches one can take toward resolving this tension: (1) concatenated representations --combine both modifiable and invariant portions of a symbol within the same representation and train DC networks to treat each portion differentially, or (2) separate pathways -- create network architectures with distinct pathways, some which alter patterns as they are propagated and some which are trained to pass the patterns along unaltered.
3.2. ID+Content Representations
Here, each symbol is viewed as consisting of two parts: (1) the ID-part contains a pattern of activation that uniquely identifies a given symbol as a unique instance of a more general class and (2) the content-part contains a pattern of activation that can be modified via symbol recirculation to carry a trace of the training tasks in which that symbol has been involved (see figure 6).
![]()
Figure 6:
ID+Content symbol representation. Each network is trained to pass on the ID-part without alteration while the content-part develops into a prototype (i.e. similar words develop content-parts with similar distributed representations).For example, the word "Bill" in the GSL would consist of both a content part, which has a pattern of activation similar to that formed for all other humans, and an ID, which uniquely identifies "Bill" as being distinct from all other humans. One can imagine, for example, that this ID represents whatever visual features are unique to the actual person named "Bill", or whatever orthographic features exist that are unique to the word "Bill".
For the ID+Content scheme to work, each DC network must be trained to pass the ID representation along without alteration, while at the same time allowing the content portion to reconstruct patterns in the output layer as usual. In order to support a large number of new IDs, the networks can be trained to autoassociate a large number of ID patterns as each content-part is being formed. Fortunately, only a small, random subset (of all possible IDs) need be trained in order for the network to properly autoassociate novel IDs. After such training, the network will accept distributed representations with different IDs and propagate these IDs without alteration, while at the same time using the content portion to reconstruct the appropriate pattern in the output layer. This technique is used to propagate script-based role bindings in DISPAR (Miikkulainen and Dyer 1989b), a connectionist script application and acquisition system (see section 4.2.2.).
3.3. Signature Activations
In this alternate approach, a pointer is represented as a unique pattern of activation and a structured connectionist network is designed, in which special pathways exist that can propagate these patterns of activation along unaltered. Using this approach, we have implemented virtual pointers in a connectionist network system designed to comprehend natural language input involving ambiguous words that require dynamic reinterpretation in subsequent contexts. The resulting system, ROBIN (Lange and Dyer 1989a,b), accomplishes its task while relying on only simple processing units (i.e. summation, summation with thresholding, and maximization). ROBIN makes use of two forms of activation.
(1) Evidential activation spreads across processing units and weighted (excitory or inhibitory) links as in other connectionist models. As in other localist models, each unit represents a semantic (or syntactic) node and the amount of evidential activation on a node represents the amount of evidence or support for that node.
(2) Signature activation is used in ROBIN to create and propagate dynamic, virtual bindings. Each instance node (e.g. JOHN) generates a unique activation value. A schema-slot node (e.g. TELL:ACTOR, which is the ACTOR slot of the TELL schema in rule R1) is bound to an instance node when its unique, signature activation value is propagated to the corresponding schema-slot node. For instance, if the signature activation for JOHN is 3.4, then the TELL:ACTOR node is considered bound to JOHN upon receiving an activation value of 3.4.
In ROBIN's localist networks there are special pathways along which signature activation is spread. These pathways connect role nodes to related frames (e.g. from TELL:TO to KNOWN:ACTOR in R1). These pathways have unit-valued weights and intervening processing units along the path act only to maximize the activations they receive as inputs. These two features serve to preserve activation values as they are propagated from a slot in one frame to another. As an example of how ROBIN processes its input, consider the following two phrases:
P1: John put the pot inside the dishwasher...
P2: because the police were coming
When ROBIN first encounters P1, it initially interprets "pot" as a COOKING-POT (versus FLOWER-POT or MARIJUANA), based on greater evidential activation spreading from "dishwasher". However, a subsequent goal/plan analysis causes ROBIN to reinterpret "pot" as MARIJUANA. This analysis is achieved through the propagation of signatures across knowledge frames, where each frame is represented in terms of nodes and weighted links between them. Just some of the bindings that must be propagated are (informally) stated as follows:
If police see actor X with illegal object O ==> then police will arrest X
If actor Z is near object O ==> then Z can see O
If actor X places O inside object Y and Y is opaque
==> then actor Z cannot see O
If actor X thinks X will be arrested by police seeing object O
==> then X will do act A to block police seeing O
This knowledge, combined with various facts (e.g. that dishwashers are opaque), leads ROBIN to conclude, via the spread of signature and evidential activation, that John has placed marijuana in the dishwasher in order to block the police seeing the marijuana, and thus achieve John's plan of avoiding arrest. As spread of activation stabilizes, the MARIJUANA interpretation of "pot" is finally selected over the other candidates, due to the higher evidential activation on MARIJUANA. Meanwhile, the representation of JOHN as the one to place the MARIJUANA inside the DISHWASHER is created through the propagation of signature activations on the slot nodes of the relevant frames in the network.
At first, it may seem that there is not enough resolution to maintain a large number of unique signatures. However, signatures need not be represented as a single value; instead, a signature can be implemented as a pattern of activation distributed over an ensemble of processing units (Lange and Dyer 1989b). Links between signature-containing nodes can be implemented as as full (or nearly full) connectivity between ensembles, where the ensembles are trained to autoassociate signatures.
4. Two Distributed Connectionist Systems for High-Level Cognitive Tasks
Given the automatic symbol formation and binding propagation techniques mentioned above, we can now begin to reimplement the kinds of NLP systems previously implemented using the addressing-by-location architecture supplied by von Neumann machines. The long-term goal of this reimplementation is to synthesize the learning, robustness and generalization features of DC systems with the structure manipulating and combinatorial capacities of traditional symbol processing systems. In addition, we hope that reimplementing the knowledge level (Newell 1981) in terms of distributed representations will lead to new insights about the nature of knowledge, its acquisition, and its relation to the tasks demanded of it.
Below we describe two connectionist architectures, DCAIN and DISPAR. In DCAIN, the structure of semantic networks is maintained, but the use of distributed representations lead to an elimination of the distinction between separate tokens and types. In DISPAR, distributed representations of scripts are automatically formed, so that the scripts formed have a much greater "richness" (i.e. statistically based context sensitivity) than symbolic scripts, while maintaining the capability of propagating script role bindings.
4.1. Representing Schemas with PDS Networks
A major problem in distributed connectionist models is that of representing structured objects, while a major problem in strictly localist connectionist networks is that of representing multiple instances (Feldman 1989). Both of these problems can be resolved by combining the structural properties of localist networks with the distributed properties of DC networks (Rumelhart et al. 1986). The result we call parallel distributed semantic (PDS) networks.
At a macroscopic level, semantic nodes are joined by semantic links to form the standard semantic networks used to represent everyday world knowledge, as is done in AI systems. At a microscopic level, however, each semantic node actually consists of an ensemble of PDP units. For example, the frame-node INGEST is represented as an ensemble of PDP units and a semantic-level connection between two semantic nodes actually consists of every PDP processing unit in one ensemble being connected to every PDP unit in the other ensemble. These connection weights are then set by an adaptive learning algorithm, such as back-error propagation .
Instances are represented very differently in a PDS network. In a semantic network, the instance "John ate a pizza" is represented by creating new symbols, say, JOHN13 and PIZZA4, and linking them into a new frame instance, e.g. INGEST8 with its own ACTOR and OBJECT slots, that inherits properties from the general INGEST, HUMAN, and FOOD frames. This approach to representing instances creates memories that are too accurate (do you remember every single meal that you have ever eaten?) and results in severe storage problems for very large episodic memories.
In contrast, instances are stored in PDS networks much as in PDP networks, i.e. as a pattern of activation distributed over the PDP units in a given ensemble. Instead of creating JOHN13, a pattern of activation is created over an ensemble that is connected to another ensemble over which INGEST8 will emerge as a pattern of activation. The connection weights between ensembles are modified (e.g. via backpropagation) so that the JOHN13 pattern in one ensemble causes the reconstruction of the INGEST8 pattern in the other ensemble (see Figure 7).
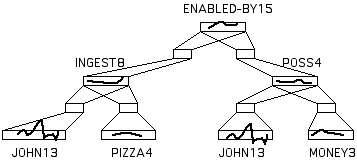
Figure 7:
A PDS network representing the knowledge that John's eating a pizza was enabled by his having money. The wavy lines are suggestive of the particular patterns of action that are currently active over the ensembles (rectangles). Each pattern of activation has been given a mnemonic name (e.g. ENABLED-BY15) for convenience. The full bidirectional connectivity between ensembles is represented by the projections to/from the hidden units (small rectangles). After the networks are trained on the given instance, the pattern ENABLED-BY15 will cause the pattern POSS4 to be reconstructed, which will then cause the patterns JOHN13 and MONEY3 to appear in the bottom right-hand ensembles.
Unlike many PDP architectures, which usually consist of a total of 3 ensembles connected in a feedforward (or simple recurrent) manner, our current PDS networks (Sumida and Dyer 1989) consist of many (hundreds, ultimately many thousands of) ensembles, connected macroscopically in a semantic network fashion. As a result, we get the structural representation capabilities of semantic networks, while retaining the generalization and reconstructive capabilities of distributed representations in PDP networks.
4.2. Distributed Script Formation and Processing
A script (Schank and Abelson 1977) is a stereotypic action sequence in a given cultural setting. Scripts have been an important theoretical construct in NLP systems, supplying a context for disambiguating word senses, resolving pronoun references, and inferring unstated events (Dyer et al. 1987). Until recently, the only implementations of script representations and script application have been symbolic in nature. An action sequence was realized as a sequence of symbolic structures, where each hand-coded structure represents a conceptual event (e.g. the diner ingesting the food).
4.2.1. Symbolic Scripts Reviewed
Symbolic scripts work very well for certain tasks, but poorly for others. For instance, Cullingford's (1981) SAM system could handle a class of pronominal references and script-based inferences extremely well. SAM could read stories of the sort:
John when to Leone's. The waiter seated him. The waiter brought him the menu. He ordered lobster. He left him a big tip.
When SAM read "John went to Leone's" it activated $RESTAURANT and bound John to the DINER role in the script $RESTAURANT. In this script there are symbolic structures representing events, somewhat like the following:
(MTRANS (ACTOR DINER)
(TO WAITER)
(C-CAUSE ANTE (PTRANS
(ACTOR WAITER)
(OBJECT FOOD)
(TO DINER))
CONSE (STATE-CHANGE
(ACTOR DINER)
(TO POSITIVE-STATE))))
This symbol structure represents the diner telling (MTRANS) the waiter that if the waiter brings (PTRANS) the food to the diner, the diner will be happy. In the lexicon, there are several patterns for "order", one of them being (informally) that [x MTRANS to y that if y DO-ACT then x will be happy]. This pattern will match the scriptal pattern above and lobster will then be bound to the FOOD role in $RESTAURANT. Once all of the script roles are bound, SAM can infer that John ate the lobster, even though the story does not explicitly state this fact. The inference is easy to make, since FOOD is already bound to lobster and DINER to John, and there is another pattern in $RESTAURANT indicating that it is the DINER (not the WAITER) who eats the FOOD. Notice that pronouns can be handled in much the same way. The sentence "he left him a big tip" produces a representation of the sort:
(ATRANS (ACTOR (ANIMATE (INSTANCE ANIMATE3)
(GENDER MALE)))
(OBJECT (MONEY (TYPE TIP)))
(TO (ANIMATE (INSTANCE ANIMATE4)
(GENDER MALE))))
which represents the abstract transfer of possession (ATRANS) of money from one male to another. This pattern is matched against the other patterns in $RESTAURANT, one of which is:
(ATRANS (ACTOR DINER)
(OBJECT (MONEY (TYPE TIP)))
(TO WAITER))
with the bindings:
DINER <--- (HUMAN
(GENDER MALE)
(NAME JOHN))
WAITER <--- (HUMAN
(GENDER MALE))
The symbolic pattern matcher will successfully match these two ATRANS patterns, since HUMAN is an member of the class ANIMATE and since the other symbols match in content and structure.
In the SAM system, there were several script paths to represent different alternative actions (e.g. not paying if the food is burnt) and several script tracks to represent different types of the same general script (e.g. fast food restaurants versus fancy restaurants). To recognize a given script required matching inputs against key portions of each script, called script headers. In the FRUMP system (Dejong 1982), for example, script headers were organized into a discrimination tree for efficient access.
These hand-coded script representations and accessing schemes never really captured the richness of even a single class of scripts. Consider the variability and context sensitivity of just the restaurant script. There are seafood restaurants, Chinese restaurants, hole-in-the-wall diners, bars that serve meals, bar-b-q restaurants, different kinds of fast-food restaurants, including fast-food Chinese restaurants, drive-thru restaurants, airport restaurants (where people often stand while they eat), and so on. As we experience more and more restaurants, we automatically form new restaurant categories and make predictions based on these categorizations. While it is relatively easy for a knowledge engineer to build a symbol-processing system that can bind an input character in a story to the DINER role, it is very difficult for that same engineer to anticipate the richness and variability that will be encountered in even such highly stereotypic experiences as scripts. The knowledge engineer cannot be expected to write rules of the sort:
If x eats at a seafood restaurant in the Malibu area
Then the restaurant will have a more impressive salad bar
and the meal will be more costly.
Instead, we want learning systems in which these kinds of rich, statistically based associations are formed automatically, and in which all these associations interact in a smooth manner to lead to an overall impression and to a set of expectations concerning experiences to follow in that context.
4.2.2. Script Acquisition and Application in DISPAR
DISPAR (Miikkulainen and Dyer 1989b) is a DC architecture that reads script-based stories and acquires distributed representations of scripts. In addition, given novel stories (i.e. involving similar scripts) as input, DISPAR performs role bindings to generate causally completed paraphrases. For example, given the story:
John went to Leone's. John asked the waiter for lobster. John gave a large tip.
DISPAR generates the paraphrase:
John went to Leone's. The waiter seated John. John asked the waiter for lobster. The waiter bought John the lobster. John ate the lobster. The lobster tasted good. John paid the waiter. John gave a large tip. John left Leone's.
DISPAR maintains a global symbol lexicon (GSL), where lexical entries are stored as distributed patterns of activation. These patterns are modified via the FGREP method (sections 2.1.1. and 2.2.), where each FGREP module also contains a recurrent hidden layer (Elman 1988), in order to handle sequences as input and output. The GSL is connected to four recurrent FGREP modules (see figure 8).
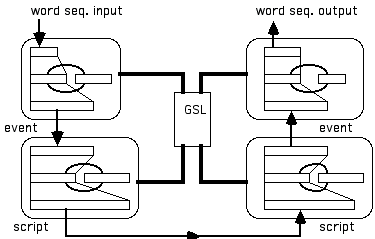
Figure 8:
DISPAR Architecture. Word sequences enter the word parser and are trained to form distributed event representations, which enter the event parser to form a distributed script representation. On the right-hand side, the process occurs in reverse; i.e., event sequences are generated from a script representation and word sequences are generated from an event representation. During both training and performance, words are taken from GSL. During training, words in GSL are modified via FGREP. The arcs in each module represent recurrent connectivity between the hidden layer and the context layer, as in Elman (1988) networks.(1) The word parser receives word sequences as input (i.e. one word at a time, taken from the GSL) and is trained (via backpropagation) to produce a case-role representation (i.e. patterns of activation for the case-roles of Actor, Object, Act, Location, etc.) in its output layer. For example, given the input sequence "John went to Leone's", the output layer is trained to place the pattern of activation for "John" in the ACTOR slot and "Leone's" in the LOCATION slot in the output layer. At the same time, using the recurrent FGREP method, the patterns of activation representing "John" and "Leone's" are altered by this training and new representations for these lexical symbols are placed back into the GSL.
(2) The event parser takes a sequence of case-role representations as input (from the word parser) and is trained to produce a script representation in its output layer. This script representation consists of set of patterns of activation over a set of script roles. For instance, here the pattern of activation for "John" would reside in the DINER slot in the output layer. Again, the learning of this mapping task causes the representation for the lexical symbol "John" to be modified via the FGREP method (sections 2.1.1. and 2.2.) and thus the representations in GSL are repeatedly updated during training.
(3) The event generator is trained to take a script representation as input and produce, in sequence on the output layer, a set of event representations (i.e. case-role associations for each event). Again, each lexical entry (e.g. "John", "the", "Leone's", etc.) is modified as a result.
(4) The word generator produces a sequence of words, one at a time, on its output layer, given a case-role representation as input. For example, given the case-role associations: [LOCATION = Leone's, ACT = went, ACTOR = John], the word generator will produce the word sequence: "John went to Leone's". Training the word generator also results in the modification of the microsemantics of each word.
When trained on a number of scripts, DISPAR automatically extracts statistical structure inherent in the data. In one experiment, for example, whenever DISPAR read about going to a fancy-restaurant, the customer left a large tip, but whenever the story involved a coffee-shop track, the tip was small. For fast-food stories, no tip was left. As a result, DISPAR automatically made these inferences when reading new stories, based on the type of script events encountered. To keep DISPAR from confusing role bindings, ID+Content representations are used (section 3.2.). The use of ID+Content representations allows one portion of a representation to become similar, while retaining a unique, unchanged portion. Thus DISPAR can be trained on stories about John, but when asked to generate a paraphrase of a new, incompletely specified story concerning Mary, DISPAR will still correctly bind the script roles with Mary. Thus, DISPAR maintains statistically "rich" representations, that are sensitive to past experience, while at the same time correctly propagating script-role bindings.
5. Comparison to Work of Others
Hinton (1986) first pointed out that one could add two additional layers, one before the input layer and one after the output layer. One could then treat the weights in these additional layers as holding representations of the I/O and view backpropagation into these additional layers as changing the representations, as is done in FGREP (Miikkulainen and Dyer 1988,. 1989a). In Hinton's model, however, there is no global symbol lexicon (GSL) and the representations formed in the input and output layers are different. As a result, the patterns formed are not accessible outside of the the network.
More recently, a number of other researchers (Pollack 1988) (Servan-Schreiber et al. 1989) (Elman 1988, 1989) have experimented with recurrent PDP networks, discovering that the patterns of activation over the hidden units form a microsemantics. In all of these systems, however, the representations for the training data are precoded by hand and remain static throughout the training; there is no GSL. As a result, it is difficult to use these systems as building blocks for constructing more complicated architectures, such as exhibited in DISPAR (Miikkulainen and Dyer 1989b).
Touretzky and Hinton (1988) have designed a DC production system that implements a rule selection and firing cycle, and which supports a limited form of variable binding. In this system (DCPS), there are only 25 possible (coarse-coded) symbols; thus a "binding space" can be set up as a Winner-Take-All (WTA) network, in which one of the 25 possible symbols will be selected, via a process of constraint satisfaction, depending on the state of working memory and the best rule selected so far. It is not clear, however, that a WTA network approach will scale up to handle the extremely large number of symbols needed for high-level cognitive tasks. The problem here is not so much whether or not WTA networks can be built that use O(n) or fewer nodes, but rather that WTA networks select from a preset, fixed number of alternatives. However, in symbol processing systems, new symbols are created dynamically, as new events occur. These dynamically created symbols are used to represent combinations of more primitive symbols. If all possible symbols must be created beforehand, as in DCPS, then enormous memories will be required for binding operations. Instead, we want to be able to create new (distributed) symbols "on the fly" as needed and then bind them using a binding mechanism that does not rely on the preexistence of a specific, static WTA structure. The use of Content+ID representations is one step in this direction, since a combinatorially large number of novel IDs can be used, once the networks using them have been trained on a small random subset of IDs. In addition, while DCPS selects a rule in a massively parallel manner, at the knowledge level, the system is sequential -- i.e. selecting and firing one rule at a time. To achieve "knowledge-level parallelism" (Sumida and Dyer 1989), DC systems must consist of many more modules. Once the architectures become more complex, issues of communication and virtual reference arise. The use of signatures (Lange and Dyer 1989a, 1989b) and PDS networks (Sumida and Dyer 1989) represent steps in this direction.
6. Future Work
As DC networks are designed to perform more high-level cognitive tasks, including planning, argumentation, word disambiguation, and question answering, more complex architectures, consisting of many, interconnect subnetworks are needed. Two major issues then arise: (a) specifying how these complex architectures could have self-organized, either through evolution, development, or learning, and (b) specifying how various DC subnetworks control and communicate with one another to accomplish various cognitive tasks. Currently, the specific cognitive models described here make use of only a subset of the techniques described. For example, the tensor manipulation networks currently do not make use of representations formed through symbol recirculation; the tensor representations are set up using microfeatures. The recurrent networks used for script acquisition and processing do not currently access PDS networks for more general goal/plan analysis, and so on. A major direction for future work, therefore, is to examine how these various symbol formation and symbol processing techniques can be integrated in a complementary manner.
Another major weakness in current high-level connectionist models is the use of overly static distributed representations. In most connectionist models, a single activation value represents the average firing rate of some idealized neuron. Real neurons, however, generate actual pulse trains (Dayhoff 1988), which can encode complex timing patterns and whose frequencies can change over time. Recent evidence suggests that the brain is a chaotic system (Skarda and Freeman 1987) and that memories, therefore, may be stored as strange attractor states (Pollack 1989). Recently, both Lange et al. (in press) and (Ajjanagadde and Shastri 1989) have proposed methods by which propagation of bindings can be realized as various forms of phase locking in the temporal dimension. Tomabechi and Kitano (1989) have proposed "frequency modulation networks" in which symbols are represented and propagated as frequency modulated pulses that are oscillated by groups of neurons. As larger models are built, based on such ideas, the resulting memories should circle around strange attractors, never passing through identical positions in state space. The knowledge that is encoded in such nonlinear, dynamical systems will be distributed both spatially and temporally.
7. Conclusions
On the one hand, symbol processing bestows on an organism the capability of making an infinite number of novel inferences. Symbols have a macrosemantics, i.e. they gain meaning through how they are related to one another. Symbol processing therefore involves the dynamic linkage of symbols to one another, at great physical distances, through virtual references. Thus, symbols are able to the represent abstract structures needed for high-level cognitive tasks, such as natural language processing. On the other hand, it is unlikely that symbols in the brain consist of static, arbitrary codes such as ASCII. It is more likely that symbols are grounded in perception and are dynamically discovered by the learner, such that their representations are intimately involved in the operations being demanded of them.
Symbol processing (SP) and distributed connectionist (DC) systems each have an important, complementary role to play. DC systems exhibit features of fault tolerance, adaptive learning, category formation, and reconstructive associative retrieval, and statistically based inferences, while traditional SP systems support logical reasoning in structural and combinatorial domains. Human cognition exhibits both of these capabilities; thus, a synthesis is in order. In this paper we have briefly examined the general approach of symbol recirculation, in which symbols start out as arbitrary patterns of activation and gradually form a microsemantics, in which symbols used in similar ways form similar distributed representations. The resulting systems exhibit better generalization and noise tolerance. We have also described three general approaches to the variable and binding propagation problems that arise in DC systems. These approaches have been used to create NLP systems capable of encoding schemas, rules, and dynamically acquiring scripts and performing script role bindings.
References
Ajjanagadde, V. and L. Shastri. Efficient Inference with Multi-Place Predicates and Variables in a Connectionist System. Proceedings of the 11th Annual Conference of the Cognitive Science Society. Lawrence Erlbaum Assoc. Hillsdale, NJ, 1989.
Bower, , G. H., Black, J. B. and T. J. Turner. Scripts in Memory for Text. Cognitive Psychology, 11, 177-220. 1979.
Charniak, E. A Neat Theory of Marker Passing. Proceedings of the Fifth National Conference on Artificial Intelligence. Morgan Kaufmann, San Mateo CA,. pp. 584-588, 1986.
Churchland, P. S. and T. J. Sejnowski. Neural Representation and Neural Computation. In L. Nadel, L. A. Cooper, P. Culicover and R. M. Harnish (eds.). Neural Connections, Mental Computation. Bradford Book, MIT Press, Cambridge MA, 1989.
Churchland, P. S. Neurophilosophy: Toward a Unified Science for Mind-Brain. MIT Press, Cambridge MA, 1986.
Cullingford, R. E. SAM. In R. C. Schank and C. K. Reisbeck (eds.). Inside Computer Understanding: Five Programs Plus Miniatures, Lawrence Erlbaum Assoc., Hillsdale NJ, pp. 75-119, 1981.
Dayhoff, J. E. Temporal Structure in Neural Networks with Impulse Train Connections. Proceedings of IEEE Second International Conference on Neural Networks. Vol. II, pp. 33-45, San Diego, 1988.
Deiderich, J. Steps towards knowledge-intensive connectionist learning. In. J. A. Barnden and J. B. Pollack (Eds.), Advances in Connectionist and Neural Computation Theory, Vol. 1, Ablex Publ., Norwood, N. J. in press.
Dolan, C. and M. G. Dyer. Symbolic Schemata, Role Binding and the Evolution of Structure in Connectionist Memories. Proceedings of the IEEE First Annual International Conference on Neural Networks. San Diego, CA, June 1987.
Dolan, C. P. and M. G. Dyer. Parallel Retrieval and Application of Conceptual Knowledge. In Touretzky, Hinton and Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summerschool. Morgan Kaufmann Publishers, San Mateo, CA. 1989.
Dolan, C. P. Tensor Manipulation Networks: Connectionist and Symbolic Approaches to Comprehension, Learning, and Planning. Ph.D. Computer Science Dept. UCLA, 1989.
DeJong II, G. F. An Overview of the FRUMP System. In W. G. Lehnert and M. H. Ringle (Eds.), Strategies for Natural Language Understanding. Lawrence Erlbaum Assoc., Hillsdale, NJ, pp. 149-176, 1982.
Dyer, M. G. In-Depth Understanding: A Computer Model of Integrated Processing for Narrative Comprehension. MIT Press. Cambridge, MA 1983.
Dyer, M. G. Symbolic NeuroEngineering for Natural Language Processing: A Multilevel Research Approach. In J. Barnden and J. Pollack (Eds.). Advances in Connectionist and Neural Computation Theory. Ablex Publ. (in press).
Dyer, M. G., Cullingford, R. & Alvarado, S. SCRIPTS. In Shapiro (ed.) Encyclopedia of Artificial Intelligence. John Wiley & Sons, 1987.
Dyer, M. G., Flowers, M. and Wang, Y. A. Distributed Symbol Discovery through Symbol Recirculation: Toward Natural Language processing in Distributed Connectionist Networks. To appear in Reilly and Sharkey (Eds.). Connectionist Approaches to Natural Language Understanding. Lawrence Erlbaum Assoc. Press, Hillsdale NJ (in press).
Elman, J. L. Finding Structure in Time. Technical Report 8801, Center for Research in Language. UCSD, San Diego. 1988.
Elman, J. L. Structured Representations and Connectionist Models. Proceedings of the 11th Annual Conference of the Cognitive Science Society. Lawrence Erlbaum Assoc. Hillsdale, NJ, pp. 17-25, 1989.
Feldman, J. A. Neural Representation of Conceptual Knowledge. In Nadel, Cooper, Culicover and Harnish (Eds.). Neural Connections, Mental Computation. MIT Press, Cambridge MA. 1989.
Fodor, J. A. and Z. W. Pylyshyn. Connectionism and Cognitive Architecture: A Critical Analysis. In Pinker and Mehler (eds.) Connections and Symbols, Bradford books/MIT Press, 1988.
Harnad, S. (Ed.) Categorial Perception: The Groundwork of Cognition. Cambridge University Press, NY. 1987.
Harnad, S. The Symbol Grounding Problem. Unpublished Manuscript, 1989.
Hendler, J. A. Integrated Marker-Passing and Problem-Solving: A Spreading Activation Approach to Improved Choice in Planning. Lawrence Erlbaum Associates, Hillsdale, NY. 1988.
Hetherington, P. A. and M. S. Seidenberg. Is There "Catastrophic Interference" in Connectionist Networks? Proceedings of the 11th Annual Conference of The Cognitive Science Society. pp. 26-33, Lawrence Erlbaum Assoc., Hillsdale, NJ. 1989.
Hinton, G. E., McClelland, J. L. and D. E. Rumelhart. Distributed Representations. In Rumelhart and McClelland. Parallel Distributed Processing, Vol. 1, Bradford Book/MIT Press. 1986.
Kohonen, T. Clustering, taxonomy, and topological maps of patterns. Proceedings of the Sixth International Conference on Pattern Recognition, IEEE Computer Society Press, 1982.
Lange, T. E. and M. G. Dyer. Dynamic, Non-Local Role Bindings and Inferencing in a Localist Network for Natural Language Understanding. In D. Touretzky (Ed.). Advances in Neural Information Processing Systems 1, Morgan Kaufmann Publ. San Mateo CA. 1989a.
Lange, T. E. and M. G. Dyer. High-Level Inferencing in a Connectionist Network. Connection Science. Vol. 1, No. 2, 1989b.
Lange, T. E., Vidal, J. J. and M. G. Dyer. Artificial Neural Oscillators for Inferencing. To appear in: Lange, T. E., Vidal, J. J. and M. G. Dyer. Artificial Neural Oscillators for Inferencing. To appear in V. I. Kryukov (ed.). Neurocomputers & Attention. Manchester University Press (in press).
Lee, G., Flowers, M. and M. G. Dyer. A Symbolic/Connectionist Script Applier Mechanism. Proceedings of the Eleventh Annual Conference of the Cognitive Science Society (CogSci-89). Ann Arbor, Michigan, 1989.
McClelland, J. L. and Kawamoto, A. H. Mechanisms of Sentence Processing: Assigning Roles to Constituents of Sentences. In McClelland and Rumelhart (eds) Parallel Distributed Processing. Vol 2, Cambridge, MA: MIT Press/Bradford Books, 1986.
Miikkulainen, R. & Dyer, M. G. Forming Global Representations with Extended Backpropagation. Proceedings of the IEEE Second Annual International Conference on Neural Networks (ICNN-88), San Diego, CA. July 1988.
Miikkulainen, R. & Dyer, M. G. Encoding Input/Output Representations in Connectionist Cognitive Systems. In Touretzky, Hinton and Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summerschool. Morgan Kaufmann Publishers, San Mateo, CA. 1989a.
Miikkulainen, R. & Dyer, M. G. A Modular Neural Network Architecture for Sequential Paraphrasing of Script-Based Stories. Proceedings of the International Joint Conference on Neural Networks (IJCNN-89). Wash. D. C. 1989b.
Minsky, M. A Framework for Representing Knowledge. In P. H. Winston (Ed.), Psychology of Computer Vision. McGraw-Hill. 1975.
Newell, A. Physical Symbol Systems. Cognitive Science Vol. 2, 1980.
Newell, A. The Knowledge Level. AI Magazine. Vol. 2, No. 2, pp. 1-20, 1981.
Pinker, S. and and Prince, A. On Language and Connectionism: Analysis of a Parallel Distributed Processing Model of Language Acquisition. In Pinker and Mehler (eds.) Connections and Symbols, Bradford books/MIT Press, 1988.
Pollack, J. Recursive Auto-Associative Memory: Devising Compositional Distributed Representations. Proceedings of the Tenth Annual Conference of the Cognitive Science Society Lawrence Erlbaum. Hillsdale, NJ, 1988.
Pollack, J. Implications of Recursive Distributed Representations. In D. S. Touretzky (Ed.) Advances in Neural Information Processing 1, Morgan Kaufmann Publ. San Mateo, CA, pp. 527-536, 1989.
Rumelhart, D. E and J. L. McClelland (Eds.) Parallel Distributed Processing: Explorations into the Microstructure of Cognition (Vols. 1 and 2). Bradford Book/MIT Press, Cambridge, MA. 1986a.
Rumelhart, D., Hinton, G. and R. Williams. Learning Internal Representations by Error Propagation. In Rumelhart & McClelland, Parallel Distributed Processing. 1986.
Schank, R. C. and R. Abelson, Scripts, Plans, Goals and Understanding, Hillsdale, NJ: LEA Press, 1977.
Schank, R. C. Dynamic Memory: A Theory of Reminding and Learning in Computers and People. NY: Cambridge University Press. 1982.
Skarda, A. and W. J. Freeman. How brains make chaos in order to make sense of the world. Behavioral and Brain Sciences. Vol. 10, No. 2, pp. 161-173, 1987.
Smolensky, P. A Method for Connectionist Variable Binding. Technical Report CU-CS-356-87, Dept. of Computer Science and Institute of Cognitive Science, Univ. of Colorado, Boulder, CO, 1987.
Smolensky, P. "On the Proper Treatment of Connectionism", The Behavioral and Brain Sciences, Vol. 11, No. 1, 1988a.
Smolensky, P. The Constituent Structure of Connectionist Mental States: A Reply to Fodor and Pylyshyn. In T. Horgan and J. Tienson (Eds.). Spindel Conference 1987: Connectionism and the Philosophy of Mind. Vol. XXVI, Supplement of The Southern Journal of Philosophy, Dept. of Philosophy, Mephis State University, 1988b.
Srinivas, K. and Barnden, J. A. Temporary Winner-Take-All Networks for Arbitray Selection in Connectionist and Neural Networks, First International Joint Conference on Neural Neworks, Washington D. C. 1989.
Sumida, R.A. and M. G. Dyer. Storing and Generalizing Multiple Instances while Maintaining Knowledge-Level Parallelism. Proceedings of the Eleventh International Joint Conference on Artificial Intelligence (IJCAI-89). Detroit, MI, 1989.
Sumida, R.A., Dyer, M.G. and M. Flowers. Integrating Marker Passing and Connectionism for Handling Conceptual and Structural Ambiguities. Proceedings of the Tenth Annual Conference of the Cognitive Science Society, Montreal, Canada, August, 1988.
Tomabechi, H. and H. Kitano. Beyond PDP: the Frequency Modulation Neural Network Architecture. Proceedings of the Eleventh International Joint Conference on Artificial Intelligence. Distributed by Morgan Kaufmann Publ. San Mateo CA, pp. 186-192, 1989.
Touretzky, D. S. Connectionism and PP Attachment. In Touretzky, Hinton and Sejnowski (Eds.). Proceedings of the 1988 Connectionist Models Summerschool. Morgan Kaufmann Publishers, San Mateo, CA. pp. 325-332, 1989.
Touretzky, D. S. and G. E. Hinton. A Distributed Connectionist Production System. Cognitive Science, 12(3), pp. 423-466, 1988.
Zernik, U. and M.G. Dyer. The Self-Extending Phrasal Lexicon. Computational Linguistics, Vol. 13, Nos. 3-4, 308-327, 1987.