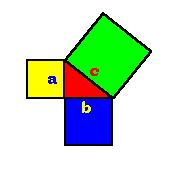El teorema de Pitágoras fue conocido por primera vez en la antigua Babilonia y Egipto (comienzos del 1900 A.C.). La relación fue demostrada en una tabla Babylonia de 4000 años, ahora conocida como Plimpton 322. Sin embargo, la relación no fue divulgada hasta que Pitágoras la enunció explicitamente.

Pitágoras vivió durante el siglo sexto A.C en la isla de Samos, en el mar Egeo. También vivió en Egipto, Babilonia y el sur de Italia. Pitágoras fué profesor y filósofo.

Pitágoras descubrió que para un triángulo rectángulo (con uno de los ángulos igual a 90°), el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados: a²+b²=c².

En otras palabras, el área cuadrada verde (con area c²) es igual a la suma de las dos otras. Es exactamente igual a el área cuadrada amarilla (a²) más el área cuadrada azul (b²).
 

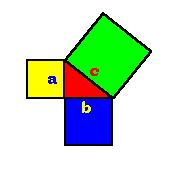
Ahora echa un vistazo a la figura de baldosas.

[La prueba del Teorema de Pitágoras está en la siguiente figura]

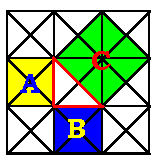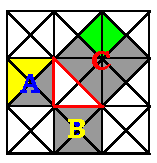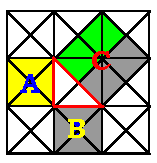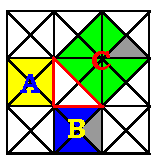
Cuenta los triángulos en cada uno de los cuadrados. El número de triángulos verdes es igual al total de los amarillos y azules!.

Sabes ...

Arqueólogos usan el Teorema de Pitágoras en sus excavaciones. Cuando comienzan una excavación, colocan una rejilla rectangular sobre la superficie a excavar. Para tener una rejilla precisa, los arqueólogos utilizan el teorema X ²+Y²=Z^{2. Trás decidir el largo de las líneas base (eje-X y eje-Y), la longitud de la diagonal es calculada utilizando el Teorema de Pitágoras para asegurarse de que el cuadrante es un rectángulo y no otro paralelogramo. En las esquinas se colocan marcas para precisar la localización.}

Una rejilla rectangular superpuesta utiliza una idea matemática llamada Sistema de Coordenadas Cartesiano.