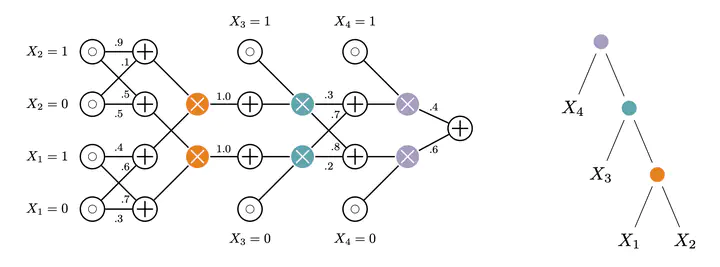
 An example of structured-decomposable probabilistic circuit and its corresponding vtree
An example of structured-decomposable probabilistic circuit and its corresponding vtree
Abstract
Probabilistic circuits (PCs) represent a probability distribution as a computational graph. Enforcing structural properties on these graphs guarantees that several inference scenarios become tractable. Among these properties, structured decomposability is a particularly appealing one: it enables the efficient and exact computations of the probability of complex logical formulas, and can be used to reason about the expected output of certain predictive models under missing data. This paper proposes Strudel, a simple, fast and accurate learning algorithm for structured-decomposable PCs. Compared to prior work for learning structured-decomposable PCs, Strudel delivers more accurate single PC models in fewer iterations, and dramatically scales learning when building ensembles of PCs. It achieves this scalability by exploiting another structural property of PCs, called determinism, and by sharing the same computational graph across mixture components. We show these advantages on standard density estimation benchmarks and challenging inference scenarios.