Home
Research
Publications
Teaching
Talks
Service
Group

The research of my lab is focused on statistical machine learning, high dimensional statistics, convex and nonconvex optimization, data mining, and their applications in text mining, recommendation systems, social and information networks, computational genomics, neuroscience, etc.

Some of our current and past research projects are

  • foundations of deep learning

  • foundations of reinforcement learning

  • nonconvex optimization

  • AI for Science

Foundations of Deep Learning

Deep learning has achieved great success in many applications such as image processing, speech recognition and Go games. However, the reason why deep learning is so powerful remains elusive. The goal of this project is to understand the successes of deep learning by studying and building the theoretical foundations of deep learning.

Generalization Theory for Deep Learning

Optimization for Deep Learning

Adversarial Learning

Nonconvex Optimization

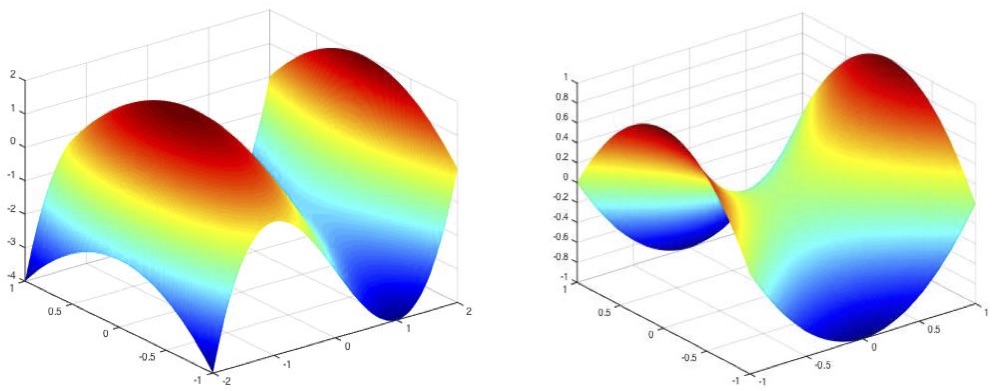
Our major research objective is to develop next generation nonconvex machine learning methods, which are based on nonconvex optimization. Nonconvex optimization naturally arises in many machine learning problems such as sparse learning, matrix and tensor factorization, graphical models and deep learning. Traditionally, nonconvexity such as nonconvex functions is considered as a curse in machine learning, because even in the optimization community, nonconvex optimization is a daunting topic. In the past decade, it is recognized that nonconvex optimization has the potential to reshape machine learning and create a new generation of machine learning theory and algorithms. However, the empirical success of nonconvex optimization cannot be well interpreted by classical statistics and optimization theory, which prohibits us from designing more efficient and effective algorithms in a systematic way. Our research aims to bridge this gap between practice and theory, by developing new nonconvex machine learning algorithms and theories. In detail, we study the following several types of nonconvex optimization problems in machine learning.

Low-Rank Matrix Learning

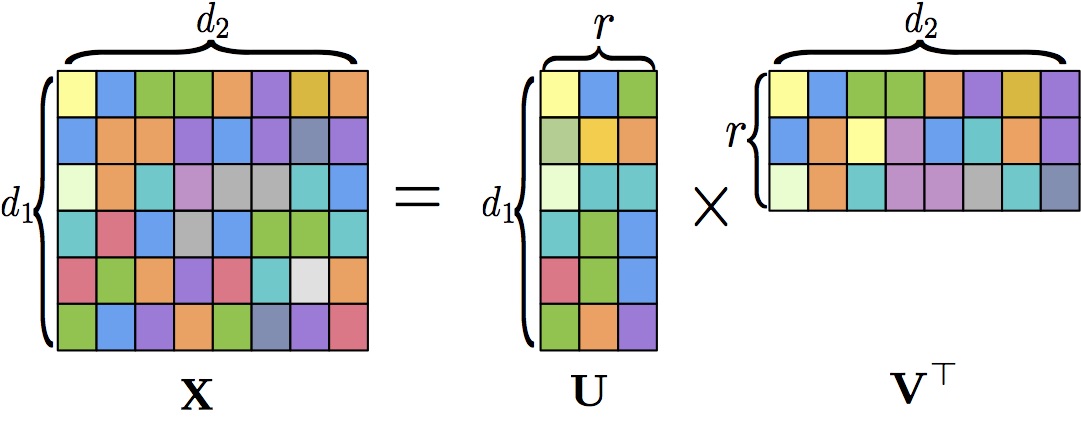
Low-rank matrix recovery problem has been extensively studied during the past decades, due to its wide range of applications, such as collaborative filtering and multi-label learning. Significant efforts have been made to estimate low-rank matrices, among which one of the most prevalent approaches is nuclear norm relaxation based optimization. While such convex relaxation based methods enjoy a rigorous theoretical guarantee to recover the unknown low-rank matrix, due to the nuclear norm regularization/minimization, these algorithms involve a singular value decomposition at each iteration, whose time complexity is cubic in the dimension of the matrix. Hence, they are computationally very expensive. In order to address the aforementioned computational issue, recent studies have been carried out to perform factorization on the matrix space, which naturally ensures the low-rankness of the produced estimator. Although this matrix factorization technique converts the previous optimization problem into a nonconvex one, which is more difficult to analyze, it significantly improves the com- putational efficiency. We develop unified computational and statistical frameworks for nonconvex low-rank (and sparse) matrix learning, with even more efficient optimization algorithms based on stochastic variance reduction and momemtum methods.

Escape from Saddle Points and Local Minima Finding

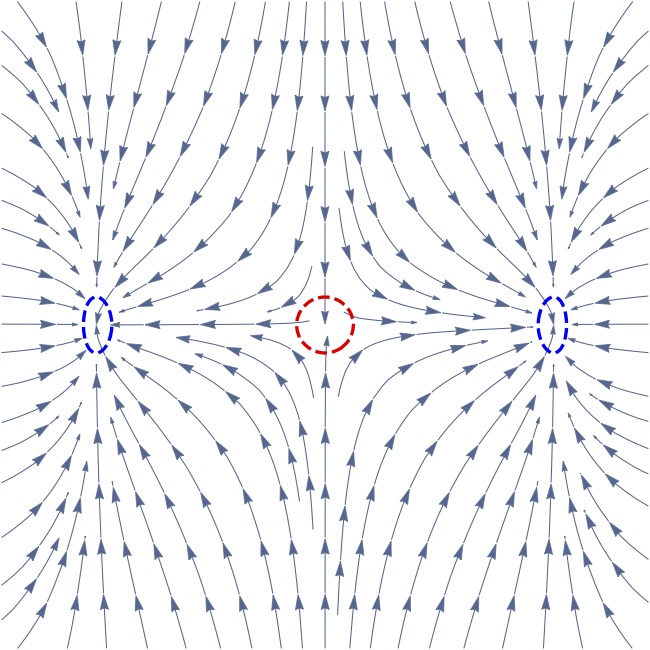
For general nonconvex optimization problems, finding a global minimum can be NP-hard. Therefore, instead of finding the global minimum, a more modest goal is to find a local minimum. In fact, for many nonconvex optimization problems in machine learning, it is sufficient to find a local minimum. Previous work in deep learning showed that a local minimum can be as good as a global minimum. Moreover, recent work showed that for some machine learning problems such as matrix completion, matrix sensing and phase retrieval, there is no spurious local minimum, i.e., all local minima are global minima. This also justifies the design of algorithms that guarantee convergence to a local minimum. We develop practical algorithms that are guaranteed to find an approximate local minimum with improved runtime complexity. The proposed algorithms are able to save gradient and negative curvature computation strikingly, and cover deterministic, stochastic and finite-sum settings.

Earlier Projects

High-Dimensional Machine Learning

High-dimensional data, where the dimension is comparable to or even larger than the sample size, are ubiquitous in modern Big Data applications, ranging from texts, images, videos, to electronic medical records, genomics data and neuroscience data. For example, neuroimaging techniques, such as functional magnetic resonance imaging (fMRI), generate massive amounts of high-resolution image datasets, which are of high dimensions (i.e., > 80,000 voxels per image). The analysis of the fMRI data can lead to important discoveries for understanding brain diseases such as Alzheimer’s disease, attention deficit, hyperactive disorder and depression. In order to learn from high-dimensional data, high-dimensional machine learning methods play a central role. At the core of high-dimensional machine learning methods is the exploitation of the intrinsic low-dimensional structure of the data, which is often achieved by imposing certain structural assumptions (e.g., sparse or low-rank) on the parameter of the underlying model.

Scalable and Robust High-Dimensional Graphical Models

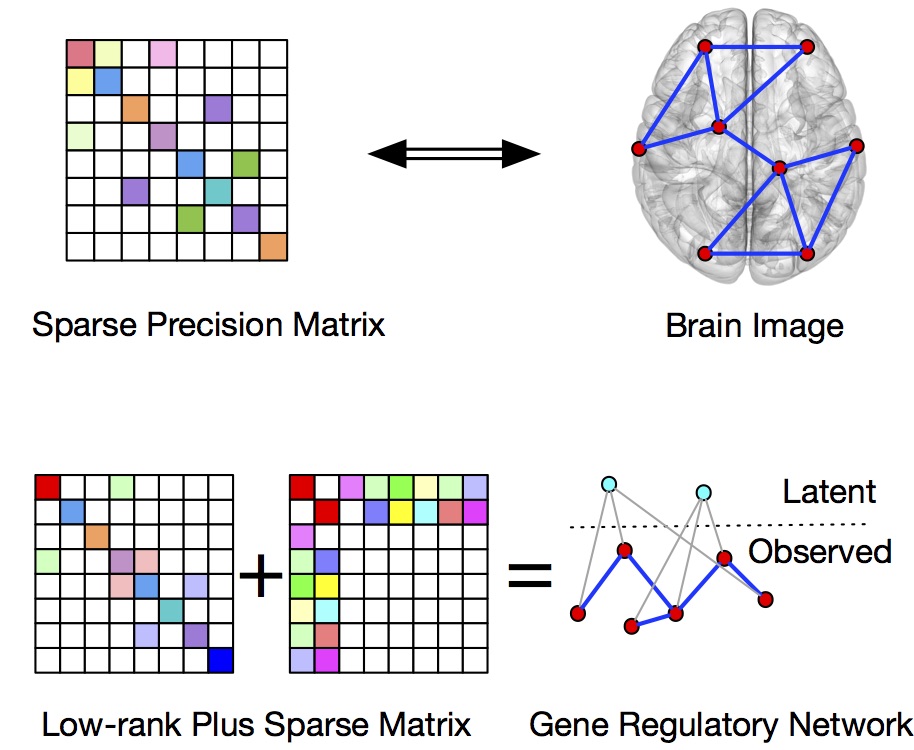
Graphical models have been widely used to explore the dependence structure of multivariate distributions. In the past decade, significant progress has been made on designing efficient estimation algorithms to learn undirected graphs from high-dimensional data. For example, Gaussian graphical model corresponds to an undirected graph, where each node corresponds to a marginal random variable, and the edge set describes the conditional independence relationships among those marginal random variables. Most of the existing estimation methods for high dimensional graphical models are based on convex optimization and are not scalable to extra-high dimensional data. Moreover, many existing methods rely on the assumption that the observations follow a Gaussian or Gaussian copula distribution. However, in many real-word applications, the data can follow a heavy-tailed distribution, or may even be corrupted arbitrarily. In such cases, conventional methods yield inaccurate graph estimation even if there are only a few contaminated observations due to the lack of robustness. We develop scalable and robust graphical model estimation methods for high-dimensional and dirty data, based on nonconvex optimization and robust statistics.

High-Dimensional Learning with Nonconvex Penalty

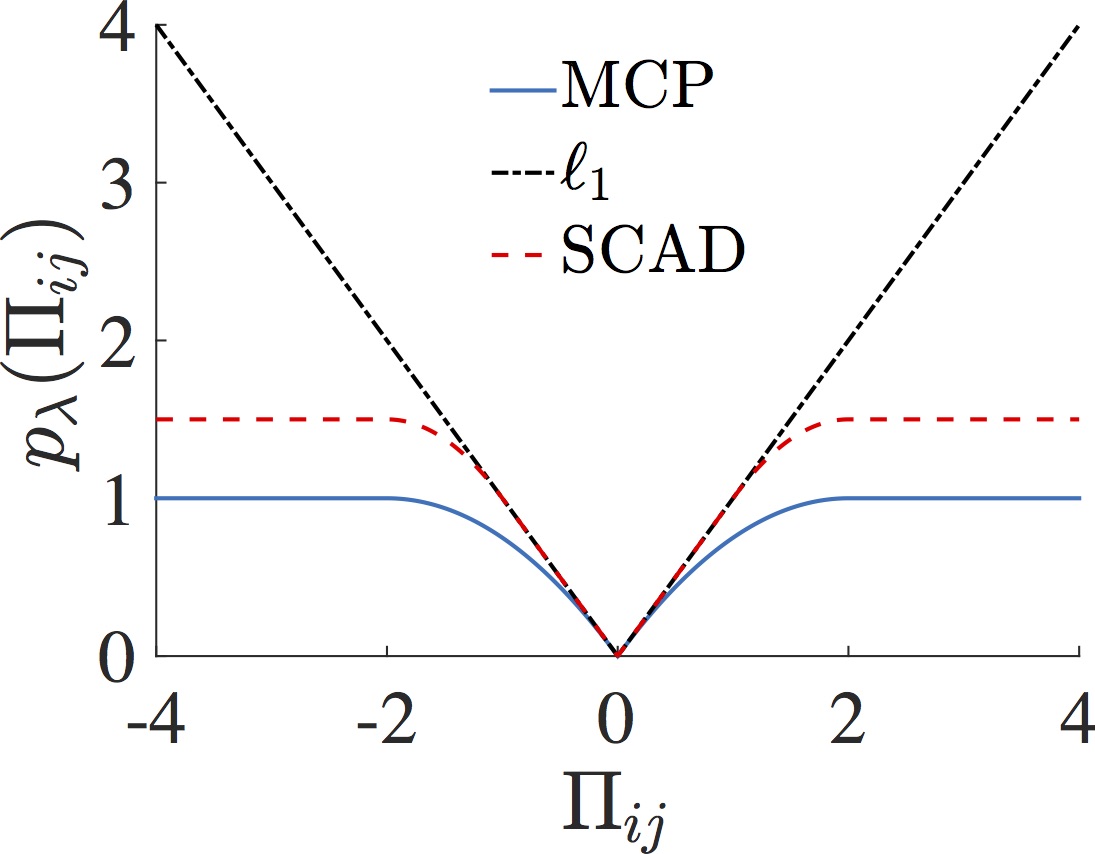
In the literature of high-dimensional statistics, it is well known that structured M-estimators with nonconvex penalties, such as MCP and SCAD, enjoy the so-called ``oracle property", which means the estimator has an optimal estimation accuracy as if the underlying structural pattern of the model parameter is known a priori. Our research shows that nonconvex penalty can also be applied to many high-dimensional machine learning models such as sparse PCA, one-bit compressed sensing, Gaussian graphical models and matrix completion/sensing, and the resulting new machine learning methods based on nonconvex penalty attain faster statistical rates of convergence and enjoy model selection consistency under much milder conditions than the state-of-the-art methods.

Structured Sparse Learning with Sparsity Constraint

The high-dimensional sparse learning problem is often cast as l1 norm regularized estimation methods such as Lasso and l1 norm regularized logistic regression. However, recent studies showed that l1 norm regularization tends to cause large estimation bias, and incur worse empirical performance than the vanilla l0 pseudo norm regularization or constraint. This motivates a family of sparsity (l0 pseudo norm) constrained or rank constrained estimators. Due to the nonconvexity of the l0 norm constraint, the resulting estimator is non-convex and in general NP hard. Thus, it is much more challenging than solving l1 norm regularized estimation problems. In order to obtain an approximate solution to this nonconvex optimization problem, many first-order optimization algorithms have been developed. We develop more efficient nonconvex (or bi-convex) optimization algorithms for this problem based on stochastic variance reduction, mini-batch block coordinate descent, inexact Newton, foward backward greedy selection and momemtum methods.

Multi-Party Secured Machine Learning with Privacy Guarantees

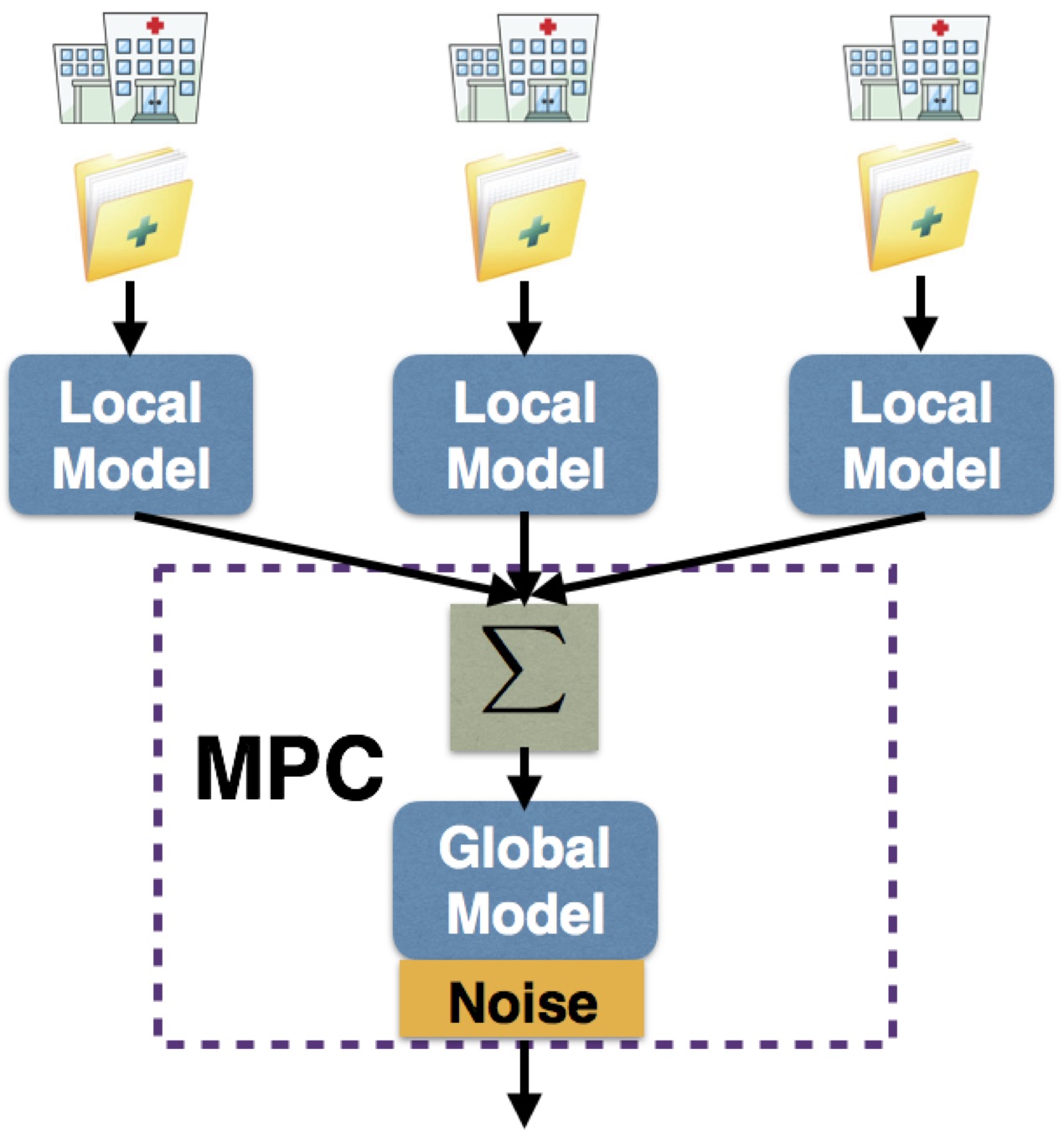
Privacy is a critical issue that one needs to address in the deployment of large-scale distributed machine learning system. Privacy protection is concerned by all individual parties, which participate in the information sharing and exchange through modern information technologies. While privacy preserving machine learning has been extensively studied, the distributed privacy preserving machine learning is still under-investigated. Working with my collaborator, we have employed a new multiparty computation protocol (i.e., Garbled Circuit) in the distributed high-dimensional machine learning for aggregating local estimators. Our work enables organizations such as hospitals and banks willing to share their data to improve the performance of data mining and management. For instance, a group of hospitals could better identify which treatments are most effective for different types of patients by aggregating medical records. Nevertheless, combining data to enable multi-institution learning is often not possible, due to privacy expectations or regulations, or may be considered too risky for a business to expose its own data to others. Our proposed framework resolves the above issue, and makes hospitals to securely collaborate to apply high-dimensional machine learning methods to produce a joint model without exposing their private medical data.

Computational Genomics

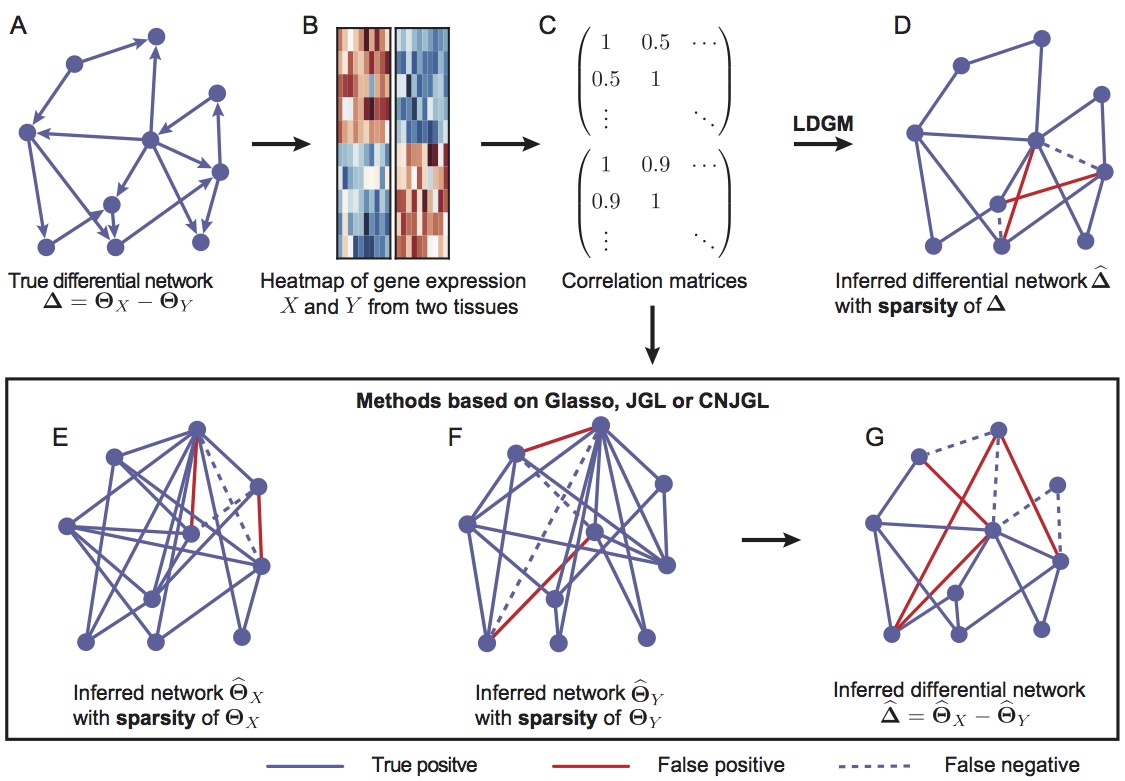
Gene regulatory networks (GRNs) are highly dynamic among different tissue types. Identifying tissue-specific gene regulation is critically important to understand gene function in a particular cellular context. Graphical models have been used to estimate GRN from gene expression data to distinguish direct interactions from indirect associations. However, most existing methods estimate GRN for a specific cell/tissue type or in a tissue-naive way, or do not specifically focus on network rewiring between different tissues. My collaborator and I proposed a new high-dimensional graphical model, called Latent Differential Graph Model (LDGM). Compared with traditional Gaussian graphical models, this new model is able to estimate the differential network between two networks directly without inferring the individual network separately, which has the advantage of utilWesizing much smaller sample size to achieve reliable differential network estimation. We have applied this innovative and powerful graphical model to study the gene regulatory network among different tissue types. This interdisciplinary study suggests that LDGM is an effective method to infer differential network using high-throughput gene expression data to identify GRN dynamics among different cellular conditions. It greatly enhances the understanding of large-scale cancer genomics data and open the door to discovering personalized molecular signature and establishing targeted treatments of cancer.

Online and Active Learning over Graphs

In order to tackle the growth and evolution of modern massive graphs, it requires learning algorithms which are able to work on the fly and adaptive to the variation of the graphs. Furthermore, since modern graphs are typically very big, online algorithms are especially appealing because they process the graph in a sequential way and therefore can be scaled up to massive networks. On the other hand, the labels of the nodes in massive graphs are scarce. It is urgent to optimize the process by which the labels are collected, because it is unrealistic to obtain the labels of every node and/or edge. Introducing active learning into massive graph data is a promising way to reduce labeling cost and allows the learning algorithm to produce an accurate predictor.

Research Support

I am very grateful to the support from National Science Foundation (IIS-1618948, CAREER IIS-1652539, IIS-1717206, SaTC CNS-1717950, BIGDATA IIS-1741342), UVa Brain Institute, UVa SEAS, Amazon Web Services, NVIDIA, Adobe and Salesforce.