We evaluate the integral expressions for the matrices
(12), (14), and
(16) numerically using Gaussian quadrature
[27]. We shall explain the computation of the element stiffness
matrix; the computation of the mass and damping matrices follow suit.
Assuming the element's parametric domain is
, the expression for entry 
of the
stiffness matrix of a D-NURBS surface element takes the integral form
where, according to (16),
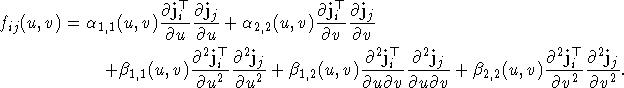
Here, the 
are the columns of the Jacobian matrix for the
D-NURBS surface element.
We apply Gaussian quadrature to compute the above integral
approximately. The integral is obtained by applying Gaussian
quadrature on the 1-D interval twice. Given integer 
and 
,
we can find Gauss weights 
, 
and abscissas 
, 
in
two directions of the parametric domain such that can be
approximated by ([27])
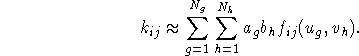
We apply the de Boor algorithm [9] to evaluate
.
Generally speaking, for integrands that are polynomial of degree
2N-1 or less, Gaussian quadrature evaluates the integral exactly
with N weights and abscissas. For D-NURBS, 
is not
polynomial unless the model is reduced to a B-spline. In our system,
we choose and to be integers between 4 and 7. Our
experiments reveal that matrices computed in this way lead to stable,
convergent solutions.