Computer Mathematics In-Progress
Computers use only two symbols, zero and one. They replace familiar
decimal numbers by strings of zeroes and ones. The quantity two looks
like a decimal ten (a one with a zero at its right). The quantity eight is a
one symbol followed at its right by three zeroes). Other quantities like
sixteen (one with four zeroes at the right) and thirty-two
(one and five zeroes) are composed taking advantage of the notion that
doubling is the same as adding another zero at the right.
The same zero/one symbols can be adjoined in ways that signal that a
non-number is represented. Some specifics are alphabetic lower-case letters,
capital letters, and punctuation marks. Even colors can be signalled by
zero/one symbols.
Here are a few challenges. They are areas to think about, things that
are more like entry points to fundamental ideas than processes to master
(like long division).
Today Computers Do Many Things
Transfer Images To People Far Away |
|
Create and Show New Patterns |
|
Support World-Wide Communication |
*Source:
http://rsd.gsfc.nasa.gov/goese/autogvar/goes8/full_earth/color/latest.color.jpg
Mathematical Concepts and Principles
Each of the following images links to a mathematical problem or concept -- click on an image to view its contents
Adding or multiplying numbers when there is no last item is a little
like the idea of the rabbit trying to catch a snail who has a one mile
head start. The puzzle goes that while the rabbit runs to the half-mile point
the snail moves forward. That means that when the rabbit makes it to the
three-quarter mile point, the seven-eighths marker, etc., there always
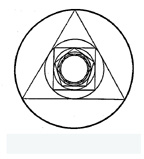
will be distance remaining to catch the snail. The same kind of
reasoning led to the view that the continually-smaller circles inside
the increasing-number-of-side polygons in the following figure get to a
smallest circle ... if we go far enough in the process. This idea is
called limit in mathematics.
Mathematical Ideas
Whether dealing with symbols or the underlying idea, mathematics deals
with aspects of the world. Some things known from the past, e.g., the circle,
go back to practical discoveries (the wheel). The symbol
π
the ratio of a circle's boundary length (circumference) to its
diameter.
Many mathematical ideas are joined to special symbols used to
concisely portray them. Sometimes the symbol blocks thinking, the
notions that led to the concepts being understood in the first place.
One such symbol is the ratio
of the length of the boundary or circumference of a circle to its diameter,
the line through the circle center which defines its widest crossing.
That quantity is called
π and pronounced by the sound pi.
Finding
π
to greater accuracy was a significant task in
mathematics up to a few hundred years ago.
Adding or multiplying numbers when there is no last item ...
a situation usually summarized in a shorthand way by the word infinite,
leads to two special symbols: Σ
represents addition while Π indicates
multiplication.
|
|
|
Computer Mathematics In-Progress |
|
|
|
|
| http://www.cs.ucla.edu/~klinger/inprogress.html |
|
|
|
|
11/19/2008 Version |
|
|
|
|