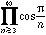
|
(9.1). |
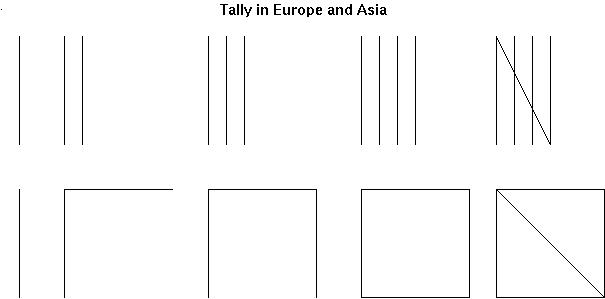
Thinking Toward Computer Basics |
||
| Sources and Credits | From elementary concepts ... | ... to computer-bafflers. |
| 25= 32 | ||
| 210=1024 | ||
| and since 264=[(25)2]6 * 24 | ||
| 264>10006 |
| n|[(2n)-3] | (8.1) |
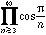
|
(9.1). |
 |
 |
| 9/27/13 Version | http://www.cs.ucla.edu/~klinger/query1.html | ©2008 Allen Klinger |