Number and Name, Sign and Symbol: How They Connect to Recalling a Concept
Allen Klinger, © 11/02/2006
A lot of names. That is just one way to describe number. Names
for how much, how many, or in terms of a concept,
quantity. Or a bunch of signs. Names for signs, in a word
symbols. Things those words enable that are
True ... and
Strange.
The words
dozen, hour, minute, and week all are names. The last three are
amounts, measures, units of time. Some names are of quantities of
any kind: words like five, six, or eight. They
give ways to say how many are present
of most objects
whether it is
eggs, minutes, seconds or days. Number-symbols are shorter than words.
They came from picturing quantity, but in many cases the symbols are far
different than those early pictures. This page deals particularly with two
quantities that are connected to digital computers.
Five
reflects the fingers of a hand, while sixteen indicates some
computers' number of ones and zeroes.
An overview table at
Sixteen lists some symbols with math and
computing language about them. The table parts can be individually
reached from the last five of
six pointers in 16_Links. Some ways of writing
sixteen are at Tallied.
The numeric symbol five repeats in the "Figure
Five in Gold" painting by Demuth, found in the New York City Metropolitan Museum
of Art. Inspired by William Carlos Williams' poem The Great Figure, the
image of fives and fire engine headlights, assigns power to the vehicle.
That power belongs to humanity's invention of numbers.
Five and sixteen, six and eight, all four are called whole or natural (both words are in use). They contrast with things like five-sixths or five-eighths that
express fractional or proportional quantities, and to
which we give the name ratios. There are many ways to write fractions.
In one place where writing began, Egypt, a dot on a symbol showed that
it was that fractional part, not that whole number. There general
fractions like five-sixths and five-eighths could not have been expressed
in a simple way (Egyptians wrote them
as sums of unit fractions like - using * for the dot - *3 + *6 +
*6 + *6 to represent what today is commonly written 5/6).
Poem-Inspired Painting

Similarly Related Art
|
The Great Figure
William Carlos Williams
Among the rain
and lights
I saw the figure 5
in gold
on a red
fire truck
moving
tense
unheeded
to gong clangs
siren howls
and wheels rumbling
through the dark city
|
Five Symbols
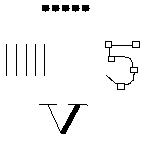 |
This link between words and an image involving numbers is natural. Both are
kinds of language, ways to communicate. Languages' kinships are detected by the
stability of their words for five, usually a synonym for hand. In
the same way that tally marks to represent a five group differently,
the Romans used a V-like five (figure above, at the right). [Tallies count
successively,
| || ||| |||| ... and then |||| with
a diagonal stroke overlay. An alternate exists:
Tallying
shows a method used in
Vietnam.
Tally and Writing shows both alongside a method used in China.
[More about numbers is at Words and
Concepts.]
Numbers came about and still act today to increase people's power in commerce.
(Getting good at business means keeping track of small differences.)
One way to view mathematics is as building on or extending numbers. There
are many mathematical concerns. They all result from thinking. That
thinking started when someone had a new idea. Nevertheless the importance, and
the actual origin of those ideas, is in solving some problem. One way to
see that notion is to consider finding the whole numbers, for instance
one through ten, or one up to eighteen, or even twenty, from simple
combining operations on exactly four fours (all must be used each time
the result is obtained). Gardner [1, p. 51] puts "simple" this way:
the arithmetical signs for addition, subtraction, multiplication, and
division together with the square-root sign (repeated as many finite
times as desired, parenthesis, decimal points and the factorial sign.
(Factorial n is written n!. It means 1 x 2 x 3 x ... x n.) A decimal
point may also be placed above .4, in which case it indicates the
repeating decimal .4444 ..., or 4/9.
For whatever reason, I gave up on finding five from four fours. Anyone
similarly inclined can see the solutions below (Fig. 7 The game of
fours, from Gardner [1, p. 52]):
 .
.
The solving a new problem notion
is true of even simple ideas like odd: sometimes all we need to
do is show something true in the case of an odd number, and then also
true when dealing with evens, to prove its universality.
The
Apples & Baskets puzzle, the second example,
tests understanding of
odd and even, the mathematical form of the idea behind digital
computers, "on or off."
Example 1. (Fractional numbers' parts.) How do we name numbers
that are parts of fractions as in 5/6? Aid available .
Example 2. (Odd and even.) How do we analyze a problem?
How can you place nine apples in four baskets so there is an odd number
of apples in each?
Cartoon Explanation.
Example 3. (Numbers, odd and even, and shapes.)
In the first century A.D. the question How can the cubes be represented
in terms of the natural numbers? was answered by the statement: Cubical
numbers are always equal to the sum of successive odd numbers and can be
represented this way.
A few examples show what this means:
13 = 1 = 1
23 = 8 = 3 + 5
33 = 7 + 9 + 11
43 = 13 + 15 + 17 + 19
Can you see why this is so? Can you give the decomposition of 73
(343) into a sum of odds? ... of 113 (1331) ??
Example 4. (Births.) What is the most probable outcome in four
births? a) Fifty-fifty male and female. b) Three of one kind, one of the
other. c) All four of the same sex. Look At It
Example 5. (Merwyn Sommer - numbers, computers.) Find the number that should follow 24 in:
10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24, __?
Little hint. Big
hint. To see what this example is
really about please click
Sequence
Answer or Short
Item on Representation. For more questions, please click
Some Problems. To see some other ways
to represent
numeric information, please click
Help Sequence?
Example 6. (Ellen Morehead - 4th grade mathematics.) "Can you divide
a circular pizza pie into eight exactly equal pieces with three straight
line cuts? Think about it."
Pizza knowledge comes in two ways. First, hard earned: Solutions. A generalization appeared in
Mathematics Magazine 41(1968), 46 (Problem 660 by L.J.
Upton) and is also in Nelsen, Roger B., Proofs Without Words II:
More Exercises in Visual Thinking, Mathematical Association of America,
2000, 27. The importance of the pizza is as a pointer to powers
(exponents): see Size.
More on mathematical things can be found
from links in Math Sources. Big numbers
(and scientific notation) are at Size. An older
version of this page is at Dozen; another is at
In Progress.
References
Gardner, Martin, The Numerology of Dr. Matrix, NY:
Simon and Schuster, 1967.
It is difficult to get the news from poems yet men die miserably every
day for lack of what is found there. -William Carlos Williams
| 11/02/06 Version |
|
|
|
|
|
http://www.cs.ucla.edu/~klinger/association.html |
|
|
|
|
©2006 Allen Klinger
|


 .
.