An Integer Linear Programming Framework for Mining Constraints from Data

An Integer Linear Programming Framework for Mining Constraints from Data

Tao Meng and Kai-Wei Chang, in ICML, 2021.

Code

Download the full text

---

Abstract

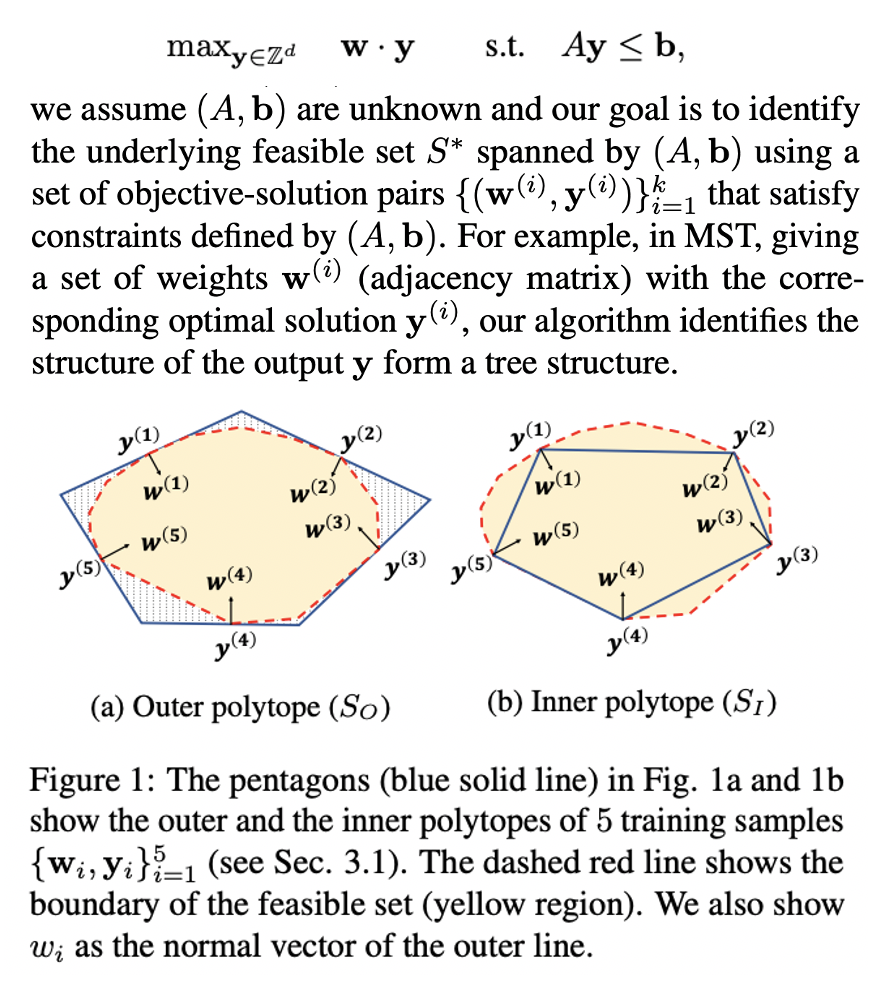
Various structured output prediction problems (e.g., sequential tagging) involve constraints over the output space. By identifying these constraints, we can filter out infeasible solutions and build an accountable model. To this end, we present a general integer linear programming (ILP) framework for mining constraints from data. We model the inference of structured output prediction as an ILP problem. Then, given the coefficients of the objective function and the corresponding solution, we mine the underlying constraints by estimating the outer and inner polytopes of the feasible set. We verify the proposed constraint mining algorithm in various synthetic and real-world applications and demonstrate that the proposed approach successfully identifies the feasible set at scale. In particular, we show that our approach can learn to solve 9x9 Sudoku puzzles and minimal spanning tree problems from examples without providing the underlying rules. We also demonstrate results on hierarchical multi-label classification and conduct a theoretical analysis on how close the mined constraints are from the ground truth.

---

---

• Video
• Source Code

---

Bib Entry

@inproceedings{meng2020integer,
  author = {Meng, Tao and Chang, Kai-Wei},
  title = {An Integer Linear Programming Framework for Mining Constraints from Data},
  booktitle = {ICML},
  year = {2021}
}

---

Related Publications

1. Relation-Guided Pre-Training for Open-Domain Question Answering

   Ziniu Hu, Yizhou Sun, and Kai-Wei Chang, in EMNLP-Finding, 2021.
   Full Text Abstract BibTeX Details

   Answering complex open-domain questions requires understanding the latent relations between involving entities. However, we found that the existing QA datasets are extremely imbalanced in some types of relations, which hurts the generalization performance over questions with long-tail relations. To remedy this problem, in this paper, we propose a Relation-Guided Pre-Training (RGPT-QA) framework. We first generate a relational QA dataset covering a wide range of relations from both the Wikidata triplets and Wikipedia hyperlinks. We then pre-train a QA model to infer the latent relations from the question, and then conduct extractive QA to get the target answer entity. We demonstrate that by pretraining with propoed RGPT-QA techique, the popular open-domain QA model, Dense Passage Retriever (DPR), achieves 2.2%, 2.4%, and 6.3% absolute improvement in Exact Match accuracy on Natural Questions, TriviaQA, and WebQuestions. Particularly, we show that RGPT-QA improves significantly on questions with long-tail relations

   @inproceedings{hu2021relation,
     title = {Relation-Guided Pre-Training for Open-Domain Question Answering},
     author = {Hu, Ziniu and Sun, Yizhou and Chang, Kai-Wei},
     presentation_id = {https://underline.io/events/192/sessions/7932/lecture/38507-relation-guided-pre-training-for-open-domain-question-answering},
     booktitle = {EMNLP-Finding},
     year = {2021}
   }
   

   Details

2. An Integer Linear Programming Framework for Mining Constraints from Data

   Tao Meng and Kai-Wei Chang, in ICML, 2021.
   Full Text Video Code Abstract BibTeX Details

   Various structured output prediction problems (e.g., sequential tagging) involve constraints over the output space. By identifying these constraints, we can filter out infeasible solutions and build an accountable model.
   To this end, we present a general integer linear programming (ILP) framework for mining constraints from data. We model the inference of structured output prediction as an ILP problem. Then, given the coefficients of the objective function and the corresponding solution, we mine the underlying constraints by estimating the outer and inner polytopes of the feasible set. We verify the proposed constraint mining algorithm in various synthetic and real-world applications and demonstrate that the proposed approach successfully identifies the feasible set at scale.
   In particular, we show that our approach can learn to solve 9x9 Sudoku puzzles and minimal spanning tree problems from examples without providing the underlying rules. We also demonstrate results on hierarchical multi-label classification and conduct a theoretical analysis on how close the mined constraints are from the ground truth.

   @inproceedings{meng2020integer,
     author = {Meng, Tao and Chang, Kai-Wei},
     title = {An Integer Linear Programming Framework for Mining Constraints from Data},
     booktitle = {ICML},
     year = {2021}
   }
   

   Details

3. Generating Syntactically Controlled Paraphrases without Using Annotated Parallel Pairs

   Kuan-Hao Huang and Kai-Wei Chang, in EACL, 2021.
   Full Text Slides Poster Code Abstract BibTeX Details

   Paraphrase generation plays an essential role in natural language process (NLP), and it has many downstream applications. However, training supervised paraphrase models requires many annotated paraphrase pairs, which are usually costly to obtain. On the other hand, the paraphrases generated by existing unsupervised approaches are usually syntactically similar to the source sentences and are limited in diversity. In this paper, we demonstrate that it is possible to generate syntactically various paraphrases without the need for annotated paraphrase pairs. We propose Syntactically controlled Paraphrase Generator (SynPG), an encoder-decoder based model that learns to disentangle the semantics and the syntax of a sentence from a collection of unannotated texts. The disentanglement enables SynPG to control the syntax of output paraphrases by manipulating the embedding in the syntactic space. Extensive experiments using automatic metrics and human evaluation show that SynPG performs better syntactic control than unsupervised baselines, while the quality of the generated paraphrases is competitive. We also demonstrate that the performance of SynPG is competitive or even better than supervised models when the unannotated data is large. Finally, we show that the syntactically controlled paraphrases generated by SynPG can be utilized for data augmentation to improve the robustness of NLP models.

   @inproceedings{huang2021generating,
     author = {Huang, Kuan-Hao and Chang, Kai-Wei},
     title = {Generating Syntactically Controlled Paraphrases without Using Annotated Parallel Pairs},
     booktitle = {EACL},
     year = {2021}
   }
   

   Details

4. Clinical Temporal Relation Extraction with Probabilistic Soft Logic Regularization and Global Inference

   Yichao Zhou, Yu Yan, Rujun Han, J. Harry Caufield, Kai-Wei Chang, Yizhou Sun, Peipei Ping, and Wei Wang, in AAAI, 2021.
   Full Text Code Abstract BibTeX Details

   There  has  been  a  steady  need  in  the  medical  community to  precisely  extract  the  temporal  relations  between  clinical events. In particular, temporal information can facilitate a variety of downstream applications such as case report retrieval and medical question answering. However, existing methods either require expensive feature engineering or are incapable of  modeling  the  global  relational  dependencies  among  theevents. In this paper, we propose Clinical Temporal Relation Exaction  with  Probabilistic  Soft  Logic  Regularization  and Global Inference (CTRL-PG), a novel method to tackle the problem at the document level. Extensive experiments on two benchmark datasets, I2B2-2012 and TB-Dense, demonstrate that CTRL-PG significantly  outperforms  baseline  methodsfor temporal relation extraction.

   @inproceedings{zhou2021clinical,
     author = {Zhou, Yichao and Yan, Yu and Han, Rujun and Caufield, J. Harry and Chang, Kai-Wei and Sun, Yizhou and Ping, Peipei and Wang, Wei},
     title = {Clinical Temporal Relation Extraction with Probabilistic Soft Logic Regularization and Global Inference},
     booktitle = {AAAI},
     year = {2021}
   }
   

   Details

5. PolicyQA: A Reading Comprehension Dataset for Privacy Policies

   Wasi Ahmad, Jianfeng Chi, Yuan Tian, and Kai-Wei Chang, in EMNLP-Finding (short), 2020.
   Full Text Code Abstract BibTeX Details

   Privacy policy documents are long and verbose. A question answering (QA) system can assist users in finding the information that is relevant and important to them. Prior studies in this domain frame the QA task as retrieving the most relevant text segment or a list of sentences from the policy document given a question. On the contrary, we argue that providing users with a short text span from policy documents reduces the burden of searching the target information from a lengthy text segment. In this paper, we present PolicyQA, a dataset that contains 25,017 reading comprehension style examples curated from an existing corpus of 115 website privacy policies. PolicyQA provides 714 human-annotated questions written for a wide range of privacy practices. We evaluate two existing neural QA models and perform rigorous analysis to reveal the advantages and challenges offered by PolicyQA.

   @inproceedings{ahmad2020policyqa,
     author = {Ahmad, Wasi and Chi, Jianfeng and Tian, Yuan and Chang, Kai-Wei},
     title = {PolicyQA: A Reading Comprehension Dataset for Privacy Policies},
     booktitle = {EMNLP-Finding (short)},
     year = {2020}
   }
   

   Details

6. GPT-GNN: Generative Pre-Training of Graph Neural Networks

   Ziniu Hu, Yuxiao Dong, Kuansan Wang, Kai-Wei Chang, and Yizhou Sun, in KDD, 2020.
   Full Text Video Code Abstract BibTeX Details Top-10 cited paper at KDD 20

   Graph neural networks (GNNs) have been demonstrated to besuccessful in modeling graph-structured data. However, training GNNs requires abundant task-specific labeled data, which is often arduously expensive to obtain. One effective way to reduce labeling effort is to pre-train an expressive GNN model on unlabelled data with self-supervision and then transfer the learned knowledge to downstream models. In this paper, we present the GPT-GNN’s framework to initialize GNNs by generative pre-training. GPT-GNN introduces a self-supervised attributed graph generation task to pre-train a GNN,which allows the GNN to capture the intrinsic structural and semantic properties of the graph. We factorize the likelihood of graph generation into two components: 1) attribute generation, and 2) edgegeneration. By modeling both components, GPT-GNN captures the inherent dependency between node attributes and graph structure during the generative process. Comprehensive experiments on thebillion-scale academic graph and Amazon recommendation data demonstrate that GPT-GNN significantly outperforms state-of-the-art base GNN models without pre-training by up to 9.1% across different downstream tasks.

   @inproceedings{hu2020gptgnn,
     author = {Hu, Ziniu and Dong, Yuxiao and Wang, Kuansan and Chang, Kai-Wei and Sun, Yizhou},
     title = {GPT-GNN: Generative Pre-Training of Graph Neural Networks},
     booktitle = {KDD},
     slide_url = {https://acbull.github.io/pdf/gpt.pptx},
     year = {2020}
   }
   

   Details

7. SentiBERT: A Transferable Transformer-Based Architecture for Compositional Sentiment Semantics

   Da Yin, Tao Meng, and Kai-Wei Chang, in ACL, 2020.
   Full Text Slides Video Code Abstract BibTeX Details

   We propose SentiBERT, a variant of BERT that effectively captures compositional sentiment semantics. The model incorporates contextualized representation with binary constituency parse tree to capture semantic composition. Comprehensive experiments demonstrate that SentiBERT achieves competitive performance on phrase-level sentiment classification. We further demonstrate that the sentiment composition learned from the phrase-level annotations on SST can be transferred to other sentiment analysis tasks as well as related tasks, such as emotion classification tasks. Moreover, we conduct ablation studies and design visualization methods to understand SentiBERT. We show that SentiBERT is better than baseline approaches in capturing negation and the contrastive relation and model the compositional sentiment semantics.

   @inproceedings{yin2020sentibert,
     author = {Yin, Da and Meng, Tao and Chang, Kai-Wei},
     title = {SentiBERT: A Transferable Transformer-Based Architecture for Compositional Sentiment Semantics},
     booktitle = {ACL},
     year = {2020},
     presentation_id = {https://virtual.acl2020.org/paper_main.341.html}
   }
   

   Details

8. Building Language Models for Text with Named Entities

   Md Rizwan Parvez, Saikat Chakraborty, Baishakhi Ray, and Kai-Wei Chang, in ACL, 2018.
   Full Text Poster Code Abstract BibTeX Details

   Text in many domains involves a significant amount of named entities. Predicting the entity names is often challenging for a language model as they appear less frequent on the training corpus. In this paper, we propose a novel and effective approach to building a language model which can learn the entity names by leveraging their entity type information. We also introduce two benchmark datasets based on recipes and Java programming codes, on which we evaluate the proposed model. Experimental results show that our model achieves 52.2% better perplexity in recipe generation and 40.3% on code generation than state-of-the-art language models.

   @inproceedings{parvez2018building,
     author = {Parvez, Md Rizwan and Chakraborty, Saikat and Ray, Baishakhi and Chang, Kai-Wei},
     title = {Building Language Models for Text with Named Entities},
     booktitle = {ACL},
     year = {2018}
   }
   

   Details

9. Learning from Explicit and Implicit Supervision Jointly For Algebra Word Problems

   Shyam Upadhyay, Ming-Wei Chang, Kai-Wei Chang, and Wen-tau Yih, in EMNLP, 2016.
   Full Text Abstract BibTeX Details

   Automatically solving algebra word problems has raised considerable interest recently. Existing state-of-the-art approaches mainly rely on learning from human annotated equations. In this paper, we demonstrate that it is possible to efficiently mine algebra problems and their numerical solutions with little to no manual effort. To leverage the mined dataset, we propose a novel structured-output learning algorithm that aims to learn from both explicit (e.g., equations) and implicit (e.g., solutions) supervision signals jointly. Enabled by this new algorithm, our model gains 4.6% absolute improvement in accuracy on the ALG-514 benchmark compared to the one without using implicit supervision. The final model also outperforms the current state-of-the-art approach by 3%.
   Dataset

   @inproceedings{BCWS16,
     author = {Upadhyay, Shyam and Chang, Ming-Wei and Chang, Kai-Wei and Yih, Wen-tau},
     title = {Learning from Explicit and Implicit Supervision Jointly For Algebra Word Problems},
     booktitle = {EMNLP},
     year = {2016}
   }
   

   Details